2D変換
変換とは、ルールを適用して一部のグラフィックを別のグラフィックに変更することを意味します。平行移動、スケールアップまたはスケールダウン、回転、せん断など、さまざまなタイプの変換を行うことができます。変換が2D平面で行われる場合、それは2D変換と呼ばれます。
変換は、コンピュータグラフィックスで重要な役割を果たし、画面上のグラフィックスの位置を変更し、サイズや向きを変更します。
同次座標
平行移動とそれに続く回転とスケーリングなどの一連の変換を実行するには、一連のプロセスに従う必要があります。
- 座標を変換し、
- 平行移動した座標を回転してから
- 回転した座標をスケーリングして、複合変換を完了します。
このプロセスを短縮するには、2×2変換行列の代わりに3×3変換行列を使用する必要があります。2×2行列を3×3行列に変換するには、ダミー座標Wを追加する必要があります。
このようにして、ポイントを2つの数字ではなく3つの数字で表すことができます。 Homogenous Coordinateシステム。このシステムでは、すべての変換方程式を行列乗算で表すことができます。任意のデカルト点P(X、Y)は、P '(X h、Y h、h)によって同次座標に変換できます。
翻訳
平行移動は、オブジェクトを画面上の別の位置に移動します。元の座標(X、Y)に平行移動座標(t x、t y)を追加して新しい座標(X '、Y')を取得することにより、2Dで点を平行移動できます。
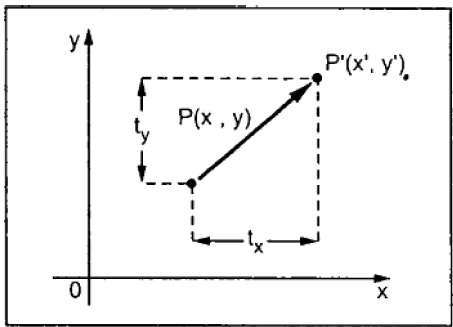
上の図から、次のように書くことができます-
X’ = X + tx
Y’ = Y + ty
ペア(t x、t y)は、平行移動ベクトルまたはシフトベクトルと呼ばれます。上記の方程式は、列ベクトルを使用して表すこともできます。
$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $
−と書くことができます
P’ = P + T
回転
回転では、オブジェクトを原点から特定の角度θ(シータ)で回転させます。次の図から、点P(X、Y)は、原点からの距離rで水平X座標から角度φに位置していることがわかります。
角度θで回転させたいとしましょう。それを新しい場所に回転させた後、新しい点P '(X'、Y ')を取得します。

標準の三角関数を使用すると、点P(X、Y)の元の座標は次のように表すことができます。
$ X = r \、cos \、\ phi ......(1)$
$ Y = r \、sin \、\ phi ......(2)$
同じように、点P '(X'、Y ')を-として表すことができます。
$ {x} '= r \:cos \:\ left(\ phi \:+ \:\ theta \ right)= r \:cos \:\ phi \:cos \:\ theta \:− \:r \ :sin \:\ phi \:sin \:\ theta .......(3)$
$ {y} '= r \:sin \:\ left(\ phi \:+ \:\ theta \ right)= r \:cos \:\ phi \:sin \:\ theta \:+ \:r \ :sin \:\ phi \:cos \:\ theta .......(4)$
式(1)と(2)をそれぞれ(3)と(4)に代入すると、次のようになります。
$ {x} '= x \:cos \:\ theta − \:y \:sin \:\ theta $
$ {y} '= x \:sin \:\ theta + \:y \:cos \:\ theta $
上記の方程式を行列形式で表すと、
$$ [X'Y '] = [XY] \ begin {bmatrix} cos \ theta&sin \ theta \\ −sin \ theta&cos \ theta \ end {bmatrix} OR $$
P '= P。R
ここで、Rは回転行列です。
$$ R = \ begin {bmatrix} cos \ theta&sin \ theta \\ −sin \ theta&cos \ theta \ end {bmatrix} $$
回転角は正と負のどちらでもかまいません。
正の回転角の場合、上記の回転行列を使用できます。ただし、負の回転角の場合、行列は次のように変化します-
$$ R = \ begin {bmatrix} cos(-\ theta)&sin(-\ theta)\\ -sin(-\ theta)&cos(-\ theta)\ end {bmatrix} $$
$$ = \ begin {bmatrix} cos \ theta&−sin \ theta \\ sin \ theta&cos \ theta \ end {bmatrix} \ left(\ since cos(− \ theta)= cos \ theta \; and \; sin(− \ theta)= −sin \ theta \ right)$$
スケーリング
オブジェクトのサイズを変更するには、スケーリング変換を使用します。スケーリングプロセスでは、オブジェクトの寸法を拡大または縮小します。スケーリングは、オブジェクトの元の座標にスケーリング係数を掛けて、目的の結果を得ることができます。
元の座標が(X、Y)、倍率が(S X、S Y)、生成された座標が(X '、Y')であると仮定します。これは、以下に示すように数学的に表すことができます-
X' = X . SX and Y' = Y . SY
スケーリングファクタS X、S YはそれぞれXおよびY方向にオブジェクトをスケーリングします。上記の方程式は、次のように行列形式で表すこともできます。
$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x}&0 \\ 0&S_ {y} \ end {bmatrix} $$
または
P’ = P . S
ここで、Sはスケーリング行列です。スケーリングプロセスを次の図に示します。
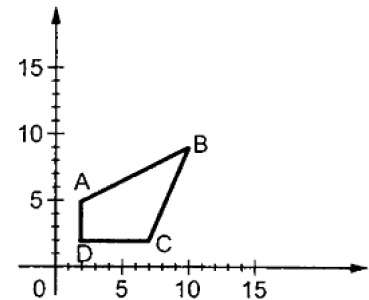
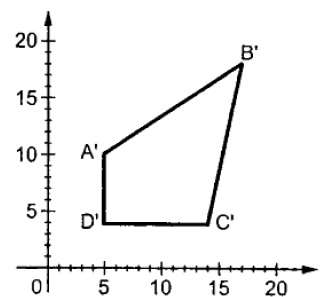
倍率Sに1未満の値を指定すると、オブジェクトのサイズを小さくすることができます。1より大きい値を指定すると、オブジェクトのサイズを大きくすることができます。
反射
反射は、元のオブジェクトの鏡像です。つまり、180°の回転操作と言えます。反射変換では、オブジェクトのサイズは変更されません。
次の図は、X軸とY軸、および原点に関する反射をそれぞれ示しています。
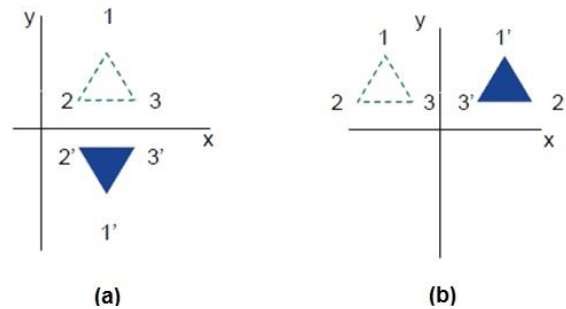
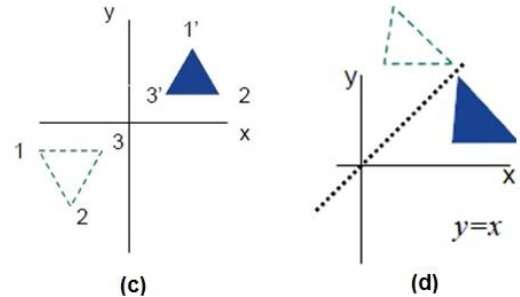
剪断
オブジェクトの形状を傾斜させる変換は、せん断変換と呼ばれます。2つのせん断変換がありますX-Shear そして Y-Shear。1つはX座標値をシフトし、もう1つはY座標値をシフトします。しかしながら; どちらの場合も、1つの座標のみがその座標を変更し、他の座標はその値を保持します。せん断は、Skewing。
X-Shear
X-ShearはY座標を保持し、X座標に変更が加えられます。これにより、下の図に示すように、垂直線が右または左に傾斜します。
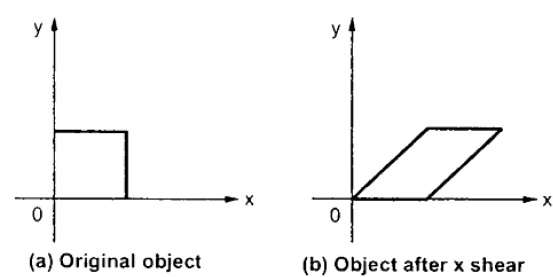
X-Shearの変換行列は、次のように表すことができます。
$$ X_ {sh} = \ begin {bmatrix} 1&shx&0 \\ 0&1&0 \\ 0&0&1 \ end {bmatrix} $$
Y」= Y + ShのY。バツ
X '= X
Yシアー
Yシアーは、X座標を保持し、Y座標を変更します。これにより、次の図に示すように、水平線が上下に傾斜する線に変換されます。
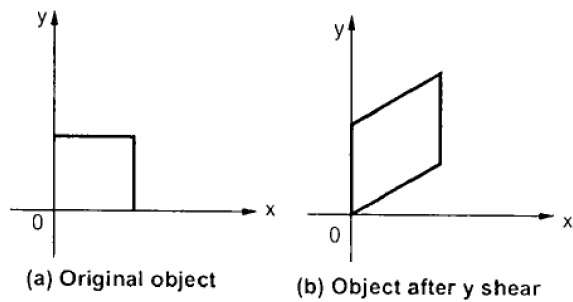
Yせん断は、次のように行列で表すことができます。
$$ Y_ {sh} \ begin {bmatrix} 1&0&0 \\ shy&1&0 \\ 0&0&1 \ end {bmatrix} $$
X」= X +のSh X。Y
Y '= Y
複合変換
平面T1の変換の後に2番目の平面変換T2が続く場合、結果自体は、T1とT2をこの順序で構成した単一の変換Tで表すことができます。これはT = T1∙T2と書かれています。
複合変換は、変換行列を連結して結合された変換行列を取得することで実現できます。
結合された行列-
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
ここで、[Ti]はの任意の組み合わせです
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
一般に行列の乗算は累積的ではないため、変換の順序を変更すると、結果が異なります。つまり、[A]です。[B]≠[B]。[A]と乗算の順序。変換を構成する基本的な目的は、一連の変換を次々に適用するのではなく、単一の構成された変換をポイントに適用することによって効率を上げることです。
たとえば、オブジェクトを任意の点(X p、Y p)を中心に回転させるには、次の3つの手順を実行する必要があります。
- 点(X p、Y p)を原点に移動します。
- 原点を中心に回転させます。
- 最後に、回転の中心を元の位置に戻します。