コンピュータグラフィックス-クイックガイド

コンピュータグラフィックスは、プログラミングの助けを借りてコンピュータ画面に絵を描く芸術です。これには、データの計算、作成、および操作が含まれます。言い換えれば、コンピュータグラフィックスは画像の生成と操作のためのレンダリングツールであると言えます。

ブラウン管

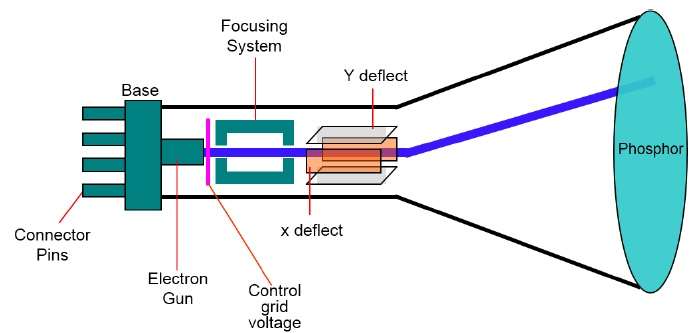
グラフィカルシステムの主要な出力デバイスはビデオモニターです。ビデオモニターの主な要素はCathode Ray Tube (CRT), 次の図に示します。

CRTの操作は非常に簡単です-

電子銃は電子ビーム（陰極線）を放出します。
電子ビームは、蛍光体でコーティングされたスクリーン上の指定された位置に向けて集束および偏向システムを通過します。
ビームがスクリーンに当たると、蛍光体は電子ビームが接触する各位置に小さなスポットの光を放出します。
電子ビームを同じスクリーンポイントにすばやく戻すことにより、画像を再描画します。

画面にオブジェクトを表示するには、2つの方法（ランダムスキャンとラスタースキャン）があります。

ラスタースキャン

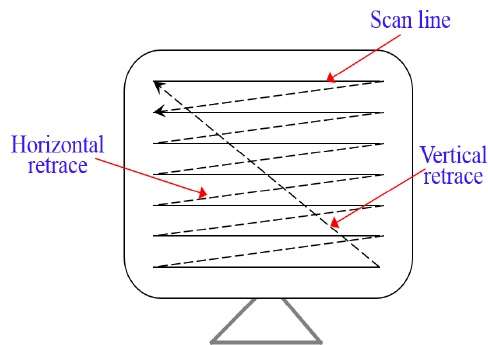
ラスタースキャンシステムでは、電子ビームは画面上を上から下に一度に1行ずつ掃引されます。電子ビームが各列を横切って移動すると、ビーム強度がオンまたはオフになり、照射スポットのパターンが作成されます。

画像定義は、と呼ばれるメモリ領域に保存されます Refresh Buffer または Frame Buffer。このメモリ領域は、すべてのスクリーンポイントの強度値のセットを保持します。次に、保存された強度値がリフレッシュバッファから取得され、次の図に示すように、一度に1行（スキャンライン）画面に「ペイント」されます。

各スクリーンポイントは、 pixel (picture element) または pel。各スキャンラインの終わりに、電子ビームは画面の左側に戻り、次のスキャンラインの表示を開始します。

ランダムスキャン（ベクタースキャン）

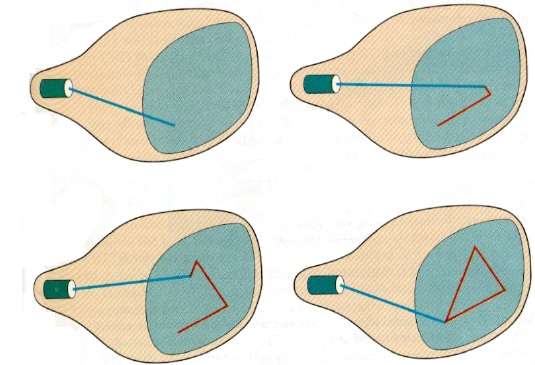
この技術では、電子ビームは、ラスタースキャンのように左から右、上から下にスキャンするのではなく、画像が描画される画面の部分にのみ向けられます。とも呼ばれますvector display, stroke-writing display, または calligraphic display。

画像の定義は、線画コマンドのセットとして、メモリの領域と呼ばれる領域に保存されます。 refresh display file。指定された画像を表示するために、システムは表示ファイル内の一連のコマンドを循環し、各コンポーネントラインを順番に描画します。すべての線画コマンドが処理された後、システムはリストの最初の線画コマンドに戻ります。

ランダムスキャンディスプレイは、画像のすべてのコンポーネントラインを毎秒30〜60回描画するように設計されています。

コンピュータグラフィックスの応用

コンピュータグラフィックスには多数のアプリケーションがあり、そのうちのいくつかを以下に示します。

Computer graphics user interfaces (GUIs) −ユーザーがコンピューターと対話できるようにするグラフィックのマウス指向のパラダイム。
Business presentation graphics −「絵は千の言葉に値する」。
Cartography −マップの描画。
Weather Maps −リアルタイムのマッピング、記号表現。
Satellite Imaging −測地線画像。
Photo Enhancement −ぼやけた写真をシャープにする。
Medical imaging − MRI、CATスキャンなど。-非侵襲的内部検査。
Engineering drawings −機械的、電気的、市民的など。-過去の青写真を置き換える。
Typography −出版におけるキャラクター画像の使用-過去のハードタイプを置き換える。
Architecture −建設計画、外観スケッチ-過去の青写真と手描きを置き換えます。
Art −コンピューターはアーティストに新しい媒体を提供します。
Training −フライトシミュレーター、コンピューター支援教育など。
Entertainment −映画とゲーム。
Simulation and modeling −物理モデリングと制定法の置き換え

線は2点を接続します。これはグラフィックスの基本的な要素です。線を引くには、線を引くことができる2つのポイントが必要です。次の3つのアルゴリズムでは、1つの線を次のように参照します。$X_{0}, Y_{0}$ 線の2番目の点は $X_{1}, Y_{1}$。

DDAアルゴリズム

デジタル微分解析機（DDA）アルゴリズムは、ここで段階的に説明される単純なライン生成アルゴリズムです。

Step 1 −2つのエンドポイントの入力を取得します $(X_{0}, Y_{0})$ そして $(X_{1}, Y_{1})$。

Step 2 −2つのエンドポイント間の差を計算します。

dx = X₁ - X₀
dy = Y₁ - Y₀

Step 3−ステップ2で計算された差に基づいて、ピクセルを配置するステップ数を特定する必要があります。dx> dyの場合、x座標でさらにステップが必要です。それ以外の場合はy座標。

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

Step 4 −x座標とy座標の増分を計算します。

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

Step 5 −それに応じてx座標とy座標を正常にインクリメントしてピクセルを配置し、線の描画を完了します。

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

ブレゼンハムのライン生成

ブレゼンハムアルゴリズムは、もう1つのインクリメンタルスキャン変換アルゴリズムです。このアルゴリズムの大きな利点は、整数計算のみを使用することです。単位間隔でx軸を横切って移動し、各ステップで2つの異なるy座標から選択します。

たとえば、次の図に示すように、位置（2、3）から、（3、3）と（3、4）のどちらかを選択する必要があります。元の線に近い点が必要です。

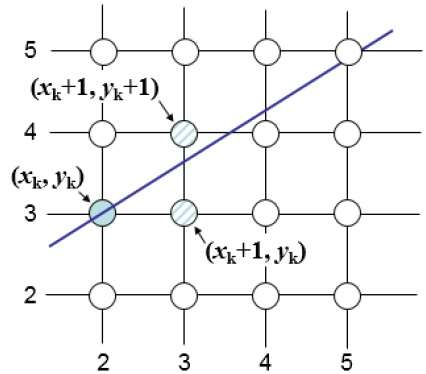
サンプル位置で $X_{k}+1,$ 数学的な線からの垂直方向の分離は、次のようにラベル付けされます $d_{upper}$ そして $d_{lower}$。

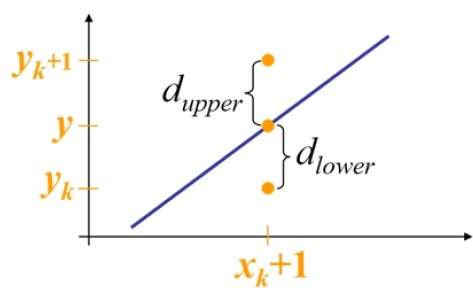
上の図から、数学的な線上のy座標は $x_{k}+1$ は−

Y = m（$X_{k}$+1）+ b

そう、 $d_{upper}$ そして $d_{lower}$ 次のように与えられます-

$$d_{lower} = y-y_{k}$$

$$= m(X_{k} + 1) + b - Y_{k}$$

そして

$$d_{upper} = (y_{k} + 1) - y$$

$= Y_{k} + 1 - m (X_{k} + 1) - b$

これらを使用して、どのピクセルが数学的な線に近いかを簡単に判断できます。この単純な決定は、2つのピクセル位置の違いに基づいています。

$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$

mをdy / dxに置き換えましょう。ここで、dxとdyはエンドポイント間の差です。

$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

だから、決定パラメータ $P_{k}$以下のためにK線に沿った目のステップは次式で与えられます-

$$p_{k} = dx(d_{lower} - d_{upper})$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

決定パラメータの符号 $P_{k}$ と同じです $d_{lower} - d_{upper}$。

場合 $p_{k}$ が負の場合は下のピクセルを選択し、そうでない場合は上のピクセルを選択します。

座標の変更はx軸に沿って単位ステップで行われるため、整数計算ですべてを実行できることを忘れないでください。ステップk + 1で、決定パラメータは次のように与えられます。

$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$

減算 $p_{k}$ これから私たちは得る-

$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$

だが、 $x_{k+1}$ と同じです $x_{k+1}$。だから−

$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$

どこ、 $Y_{k+1} – Y_{k}$ の符号に応じて0または1のいずれかです $P_{k}$。

最初の決定パラメーター $p_{0}$ で評価されます $(x_{0}, y_{0})$ −として与えられます

$$p_{0} = 2dy - dx$$

ここで、上記のすべての点と計算を念頭に置いて、勾配m <1 −のブレゼンハムアルゴリズムを次に示します。

Step 1 −線の2つの端点を入力し、左側の端点をに格納します。 $(x_{0}, y_{0})$。

Step 2 −点をプロットします $(x_{0}, y_{0})$。

Step 3 −定数dx、dy、2dy、および（2dy – 2dx）を計算し、決定パラメーターの最初の値を−として取得します。

$$p_{0} = 2dy - dx$$

Step 4 −それぞれで $X_{k}$ 線に沿って、k = 0から開始して、次のテストを実行します-

場合 $p_{k}$ <0、プロットする次のポイントは $(x_{k}+1, y_{k})$ そして

$$p_{k+1} = p_{k} + 2dy$$ そうでなければ、

$$(x_{k}, y_{k}+1)$$

$$p_{k+1} = p_{k} + 2dy - 2dx$$

Step 5 −手順4（dx – 1）を繰り返します。

m> 1の場合、毎回yをインクリメントしながらxをインクリメントする必要があるかどうかを調べます。

解いた後、決定パラメータの方程式 $P_{k}$ 非常によく似ていますが、方程式のxとyだけが交換されます。

中間点アルゴリズム

中間点アルゴリズムは、PittewayとVanAkenによって変更されたBresenhamによるものです。次の図に示すように、点Pを（x、y）座標に配置し、線の傾きが0≤k≤1であると仮定します。

次に、次の点をEまたはNのどちらに配置するかを決定する必要があります。これは、点NまたはEに最も近い交点Qを特定することで選択できます。交点Qが点Nに最も近い場合、Nは次のように見なされます。次のポイント。それ以外の場合はE。

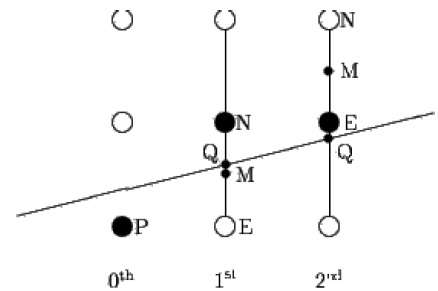
それを決定するには、最初に中点M（x + 1、y +½）を計算します。EとNを結ぶ垂直線との線の交点QがMの下にある場合は、Eを次の点とします。それ以外の場合は、次の点としてNを取ります。

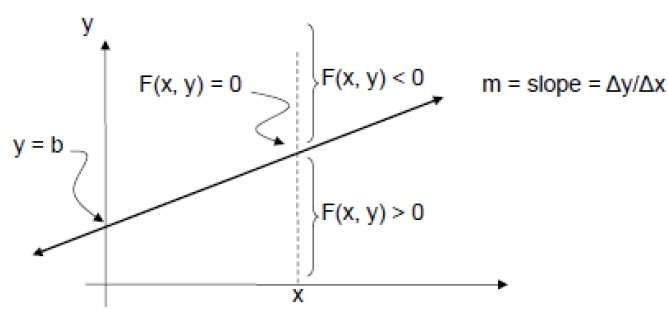
これをチェックするために、暗黙の方程式を考慮する必要があります-

F（x、y）= mx + b-y

任意のXで正のmの場合、

yが線上にある場合、F（x、y）= 0
yが線より上にある場合、F（x、y）<0
yが線より下にある場合、F（x、y）> 0

画面に円を描くことは、線を描くことよりも少し複雑です。円を生成するための2つの一般的なアルゴリズムがあります-Bresenham’s Algorithm そして Midpoint Circle Algorithm。これらのアルゴリズムは、円を描くために必要な後続のポイントを決定するという考えに基づいています。アルゴリズムについて詳しく説明しましょう-

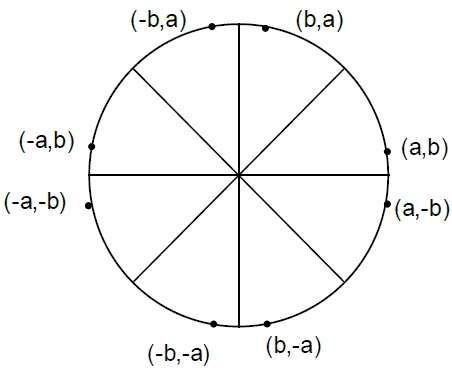
円の方程式は $X^{2} + Y^{2} = r^{2},$ ここで、rは半径です。

ブレゼンハムのアルゴリズム

ラスター表示で連続円弧を表示することはできません。代わりに、アークを完成させるために最も近いピクセル位置を選択する必要があります。

次の図から、ピクセルを（X、Y）の位置に配置し、次のピクセルを配置する場所を決定する必要があることがわかります-N（X + 1、Y）またはS（X + 1、 Y-1）。

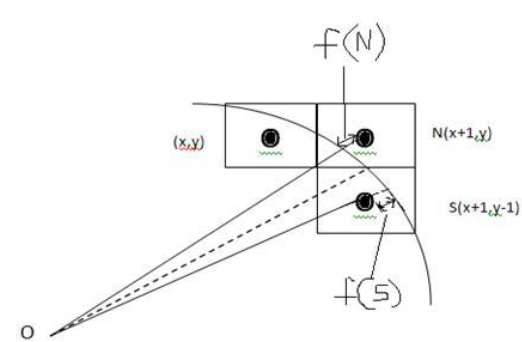
これは決定パラメータによって決定できます d。

d <= 0の場合、次のピクセルとしてN（X + 1、Y）が選択されます。
d> 0の場合、S（X + 1、Y-1）が次のピクセルとして選択されます。

アルゴリズム

Step 1−円の中心と半径の座標を取得し、それぞれx、y、Rに格納します。P = 0およびQ = Rに設定します。

Step 2 −決定パラメータD = 3 –2Rを設定します。

Step 3 −P≤Qの間、ステップ8を繰り返します。

Step 4 − Draw Circle（X、Y、P、Q）を呼び出します。

Step 5 −Pの値をインクリメントします。

Step 6 − D <0の場合、D = D + 4P +6。

Step 7 −その他のセットR = R -1、D = D + 4（PQ）+10。

Step 8 − Draw Circle（X、Y、P、Q）を呼び出します。

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

ミッドポイントアルゴリズム

Step 1 −入力半径 r とサークルセンター $(x_{c,} y_{c})$ 原点を中心とする円周上の最初の点を次のように取得します。

(x₀, y₀) = (0, r)

Step 2 −決定パラメータの初期値を次のように計算します。

$P_{0}$ = 5/4 – r（この式の簡略化については、次の説明を参照してください。）

f(x, y) = x² + y² - r² = 0

f(x_i - 1/2 + e, y_i + 1)
        = (x_i - 1/2 + e)² + (y_i + 1)² - r² 
        = (x_i- 1/2)² + (y_i + 1)² - r² + 2(x_i - 1/2)e + e²
        = f(x_i - 1/2, y_i + 1) + 2(x_i - 1/2)e + e² = 0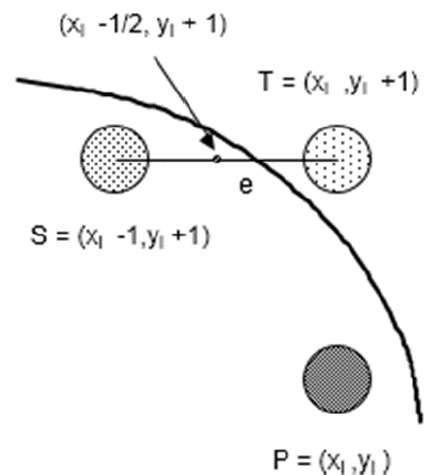

Let d_i = f(x_i - 1/2, y_i + 1) = -2(x_i - 1/2)e - e²
Thus,

If e < 0 then di > 0 so choose point S = (x_i - 1, y_i + 1).
d_i+1    = f(x_i - 1 - 1/2, y_i + 1 + 1) = ((x_i - 1/2) - 1)² + ((y_i + 1) + 1)² - r²
        = d_i - 2(x_i - 1) + 2(y_i + 1) + 1
        = d_i + 2(y_{i + 1} - x_{i + 1}) + 1
		  
If e >= 0 then di <= 0 so choose point T = (x_i, y_i + 1)
   d_i+1 = f(x_i - 1/2, y_i + 1 + 1)
       = d_i + 2y_i+1 + 1
		  
The initial value of di is
   d₀ = f(r - 1/2, 0 + 1) = (r - 1/2)² + 1² - r²
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (x_i - 1, y_i + 1) is chosen then
   d_i+1 = d_i + -2x_i+1 + 2y_i+1 + 1
	
When point T = (x_i, y_i + 1) is chosen then
   d_i+1 = d_i + 2y_i+1 + 1

Step 3 −それぞれで $X_{K}$ K = 0から始まる位置で、次のテストを実行します-

If P_K < 0 then next point on circle (0,0) is (X_K+1,Y_K) and
   P_K+1 = P_K + 2X_K+1 + 1
Else
   P_K+1 = P_K + 2X_K+1 + 1 – 2Y_K+1
	
Where, 2X_K+1 = 2X_K+2 and 2Y_K+1 = 2Y_K-2.

Step 4 −他の7つの八分円の対称点を決定します。

Step 5 −各計算ピクセル位置（X、Y）を中心の円形パスに移動します $(X_{C,} Y_{C})$ 座標値をプロットします。

X = X + X_C,   Y = Y + Y_C

Step 6 − X> = Yになるまで、手順3〜5を繰り返します。

ポリゴンは、次の図に示すように、頂点の順序付きリストです。ポリゴンを特定の色で塗りつぶすには、ポリゴンの境界にあるピクセルとポリゴンの内側にあるピクセルを決定する必要があります。この章では、さまざまな手法を使用してポリゴンを塗りつぶす方法を説明します。

スキャンラインアルゴリズム

このアルゴリズムは、スキャンラインをポリゴンエッジと交差させることで機能し、交差のペア間でポリゴンを塗りつぶします。次の手順は、このアルゴリズムがどのように機能するかを示しています。

Step 1 −指定されたポリゴンからYminとYmaxを見つけます。

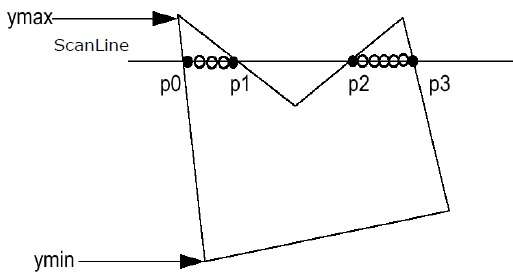
Step 2− ScanLineは、YminからYmaxまでのポリゴンの各エッジと交差します。ポリゴンの各交点に名前を付けます。上図のように、p0、p1、p2、p3という名前が付けられています。

Step 3 − X座標の昇順、つまり（p0、p1）、（p1、p2）、および（p2、p3）で交点を並べ替えます。

Step 4 −ポリゴン内にある座標のペアをすべて埋め、代替ペアを無視します。

フラッドフィルアルゴリズム

エリアとその境界を異なる色で塗りつぶしたいオブジェクトに出くわすことがあります。境界塗りつぶしアルゴリズムのように特定の境界色を検索する代わりに、指定された内部色でそのようなオブジェクトをペイントできます。

オブジェクトの境界に依存する代わりに、塗りつぶしの色に依存します。つまり、オブジェクトの内部の色を塗りつぶしの色に置き換えます。元の内部色のピクセルがなくなると、アルゴリズムが完了します。

繰り返しになりますが、このアルゴリズムは、ピクセルを埋める4接続または8接続の方法に依存しています。ただし、境界色を探す代わりに、内部の一部である隣接するすべてのピクセルを探します。

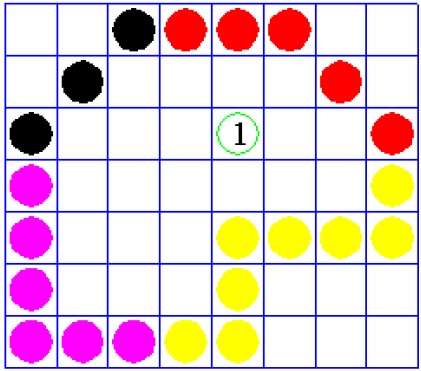
境界塗りつぶしアルゴリズム

境界塗りつぶしアルゴリズムはその名前として機能します。このアルゴリズムは、オブジェクト内のポイントを選択し、オブジェクトの境界に到達するまで塗りつぶしを開始します。このアルゴリズムが機能するには、境界の色と塗りつぶす色が異なっている必要があります。

このアルゴリズムでは、境界の色がオブジェクト全体で同じであると想定しています。境界塗りつぶしアルゴリズムは、4接続ピクセルまたは8接続ピクセルで実装できます。

4-接続されたポリゴン

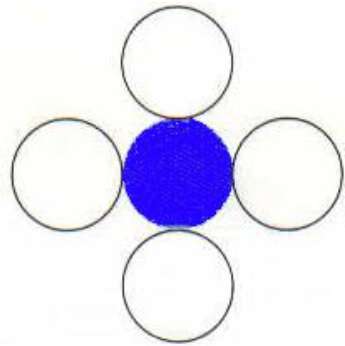
この手法では、図に示すように4つの接続されたピクセルが使用されます。現在のピクセルの上、下、右、および左側にピクセルを配置しています。このプロセスは、異なる色の境界が見つかるまで続行されます。

アルゴリズム

Step 1 −シードポイント（seedx、seedy）、fcolor、およびdcolの値を初期化します。

Step 2 −ポリゴンの境界値を定義します。

Step 3 −現在のシードポイントがデフォルトの色であるかどうかを確認し、境界ピクセルに達するまで手順4と5を繰り返します。

If getpixel(x, y) = dcol then repeat step 4 and 5

Step 4 −シードポイントの塗りつぶし色でデフォルトの色を変更します。

setPixel(seedx, seedy, fcol)

Step 5 −4つの近隣点を使用して手順を再帰的に実行します。

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)

Step 6 −終了

この手法には問題があります。以下に示すように、領域全体を埋めようとした場合を考えてみます。ここでは、画像は部分的にしか塗りつぶされていません。このような場合、4接続ピクセル技術は使用できません。

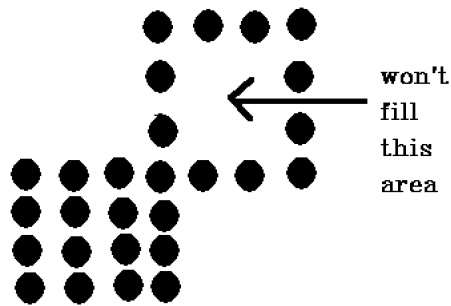
8-接続されたポリゴン

この手法では、図に示すように8つの接続されたピクセルが使用されます。4接続手法で行っていたように、現在のピクセルの上、下、右側、左側にピクセルを配置しています。

これに加えて、現在のピクセルの全領域がカバーされるように、ピクセルを対角線上に配置しています。このプロセスは、異なる色の境界が見つかるまで続きます。

アルゴリズム

Step 1 −シードポイント（seedx、seedy）、fcolor、およびdcolの値を初期化します。

Step 2 −ポリゴンの境界値を定義します。

Step 3 −現在のシードポイントがデフォルトの色であるかどうかを確認し、境界ピクセルに達するまで手順4と5を繰り返します。

If getpixel(x,y) = dcol then repeat step 4 and 5

Step 4 −シードポイントの塗りつぶし色でデフォルトの色を変更します。

setPixel(seedx, seedy, fcol)

Step 5 −4つの近隣点を使用して手順を再帰的に実行します

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)

Step 6 −終了

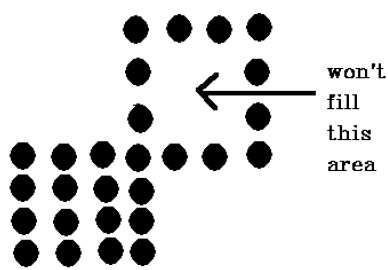
次の図に示すように、4接続ピクセル手法では領域を埋めることができませんでした。これは8接続手法では発生しません。

内外テスト

この方法は、 counting number method。オブジェクトを塗りつぶすときに、特定のポイントがオブジェクトの内側にあるか外側にあるかを識別する必要があることがよくあります。特定のポイントがオブジェクトの内側にあるか外側にあるかを識別するには、2つの方法があります。

奇数-偶数ルール
非ゼロの回転数規則

奇数-偶数ルール

この手法では、任意の点（x、y）から無限大までの線に沿って交差するエッジをカウントします。相互作用の数が奇数の場合、点（x、y）は内部点です。相互作用の数が偶数の場合、点（x、y）は外部点です。これはあなたに明確な考えを与えるための例です-

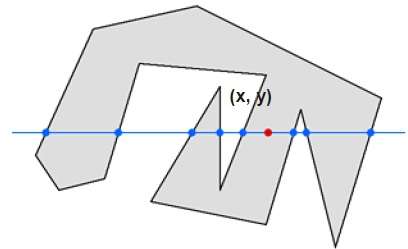
上の図から、点（x、y）から、左側の相互作用点の数は5、右側の相互作用点の数は3であることがわかります。したがって、相互作用点の総数は8であり、奇数です。。したがって、ポイントはオブジェクト内で考慮されます。

ゼロ以外の回転数ルール

この方法は、特定のポイントが内部であるかどうかをテストするために、単純なポリゴンでも使用されます。ピンと輪ゴムで簡単に理解できます。ポリゴンの端の1つにピンを固定し、その中に輪ゴムを結び、ポリゴンの端に沿って輪ゴムを伸ばします。

ポリゴンのすべてのエッジが輪ゴムで覆われている場合は、テストするポイントで固定されているピンを確認します。ポイントで少なくとも1つの風が見つかった場合は、それをポリゴン内と見なします。それ以外の場合、ポイントはポリゴン内にないと言えます。

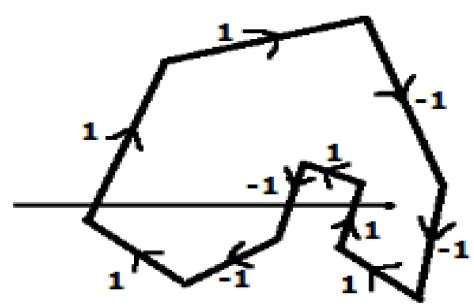
別の代替方法では、ポリゴンのすべてのエッジに方向を指定します。テストするポイントからX方向の左端に向かってスキャンラインを描画します。

上方向に向かうすべてのエッジに値1を指定し、方向の値として他のすべての-1を指定します。
スキャンラインが通過するエッジ方向の値を確認し、それらを合計します。
この方向の値の合計がゼロ以外の場合、テストされるこのポイントは interior point, それ以外の場合は exterior point。
上の図では、スキャンラインが通過する方向の値を合計すると、合計は1 – 1 + 1 = 1になります。これはゼロ以外です。したがって、ポイントは内部ポイントと呼ばれます。

コンピュータグラフィックスでのクリッピングの主な用途は、表示ペインの外側にあるオブジェクト、線、または線分を削除することです。表示変換は、表示ボリュームに対するポイントの位置（特にビューアの後ろのポイント）の影響を受けないため、ビューを生成する前にこれらのポイントを削除する必要があります。

ポイントクリッピング

特定のウィンドウからポイントをクリップするのは非常に簡単です。次の図を考えてみましょう。長方形はウィンドウを示しています。ポイントクリッピングは、指定されたポイント（X、Y）が指定されたウィンドウ内にあるかどうかを示します。そして、ウィンドウの最小座標と最大座標を使用するかどうかを決定します。

XがWx1≤X≤Wx2の間にある場合、指定されたポイントのX座標はウィンドウの内側にあります。同様に、YがWy1≤Y≤Wy2の間にある場合、指定された点のY座標はウィンドウの内側にあります。

線クリッピング

ラインクリッピングの概念は、ポイントクリッピングと同じです。線クリッピングでは、ウィンドウの外側にあるラインの部分をカットし、ウィンドウの内側にある部分のみを保持します。

コーエン-サザランドラインクリッピング

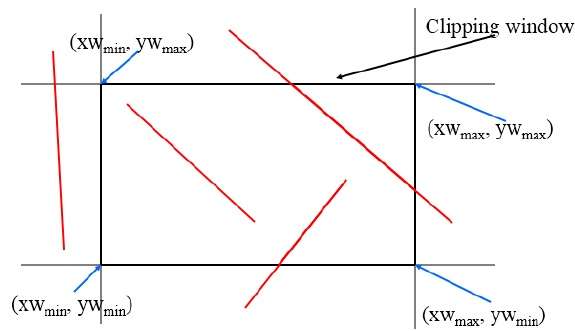
このアルゴリズムは、次の図に示すようにクリッピングウィンドウを使用します。クリッピング領域の最小座標は$(XW_{min,} YW_{min})$ クリッピング領域の最大座標は $(XW_{max,} YW_{max})$。

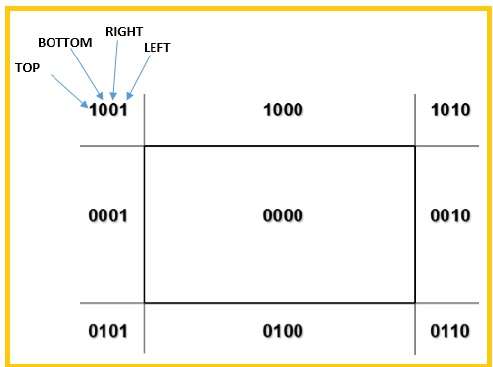
領域全体を分割するために4ビットを使用します。これらの4ビットは、次の図に示すように、領域の上部、下部、右側、および左側を表します。ここでは、TOP そして LEFT ビットは1に設定されているため、 TOP-LEFT コーナー。

ラインには3つの可能性があります-

線は完全にウィンドウの内側に置くことができます（この線は受け入れられる必要があります）。
線は完全にウィンドウの外側に置くことができます（この線は領域から完全に削除されます）。
線は部分的にウィンドウの内側に配置できます（交点を見つけて、領域内にある線の部分のみを描画します）。

アルゴリズム

Step 1 −各エンドポイントにリージョンコードを割り当てます。

Step 2 −両方のエンドポイントにリージョンコードがある場合 0000 次に、この行を受け入れます。

Step 3 −それ以外の場合は、論理を実行します AND両方のリージョンコードの操作。

Step 3.1 −結果がそうでない場合 0000, 次に、その行を拒否します。

Step 3.2 −それ以外の場合は、クリッピングが必要です。

Step 3.2.1 −ウィンドウの外側にある線の端点を選択します。

Step 3.2.2 −ウィンドウ境界で交点を見つけます（地域コードに基づく）。

Step 3.2.3 −端点を交点に置き換え、地域コードを更新します。

Step 3.2.4 −簡単に受け入れられるか、簡単に拒否されるクリップされた行が見つかるまで、手順2を繰り返します。

Step 4 −他の行についても手順1を繰り返します。

Cyrus-Beckラインクリッピングアルゴリズム

このアルゴリズムは、コーエン-サザランドアルゴリズムよりも効率的です。パラメトリックライン表現と単純なドット積を採用しています。

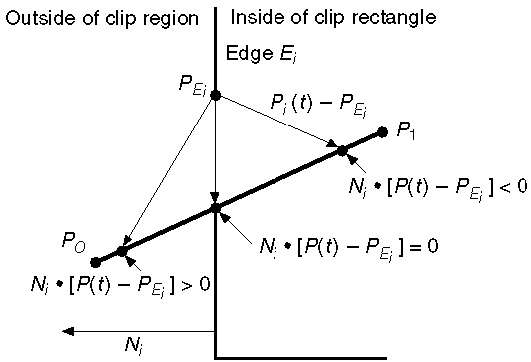
直線のパラメトリック方程式は−

P₀P₁:P(t) = P₀ + t(P₁-P₀)

ましょうN_私は外側に、通常のエッジEも_私。今、任意の点Pピック_EiのエッジE上の_I次いで内積N _I ∙[P（T） - P _Eiは】点P（t）があるか否かを判断又は「外側」クリップエッジ「クリップエッジ内側」またはクリップの端に「オン」。

N _i。[P（t）– P _Ei ] <0の場合、点P（t）は内側にあります。

N _i。[P（t）– P _Ei ]> 0の場合、点P（t）は外側にあります。

N _i。[P（t）– P _Ei ] = 0（交点）の場合、点P（t）はエッジ上にあります。

N _i。[P（t）– P _Ei ] = 0

N _I [P。₀ + T（P ₁ -P ₀） - P _Eiは] = 0（PとP（t）を交換₀ + T（P ₁ -P ₀））

N _I [P。₀ - P _Eiの] + N _I .T [P ₁ -P ₀ ] = 0

N _I。[P ₀ - P _Eiの] + N _iは∙tDの= 0（代用D [P ₁ -P ₀ ]）

N _I [P。₀ - P _Eiの] = - N _I ∙tDの

tの式は次のようになります。

$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$

以下の条件で有効です-

N _i ≠0（エラーは発生しません）
D≠0（P ₁ ≠P ₀）
N _I ∙D≠0（P ₀ P ₁ Eと平行でない_I）

ポリゴンクリッピング（Sutherland Hodgmanアルゴリズム）

クリッピングウィンドウを指定して、ポリゴンをクリッピングすることもできます。ポリゴンクリッピングには、SutherlandHodgemanポリゴンクリッピングアルゴリズムが使用されます。このアルゴリズムでは、ポリゴンのすべての頂点がクリッピングウィンドウの各エッジに対してクリッピングされます。

まず、ポリゴンをポリゴンウィンドウの左端にクリップして、ポリゴンの新しい頂点を取得します。これらの新しい頂点は、次の図に示すように、クリッピングウィンドウの右端、上端、下端に対してポリゴンをクリップするために使用されます。

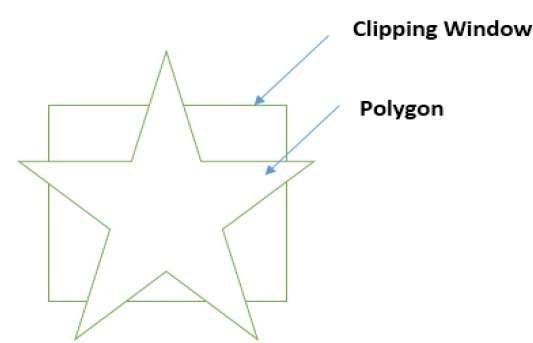
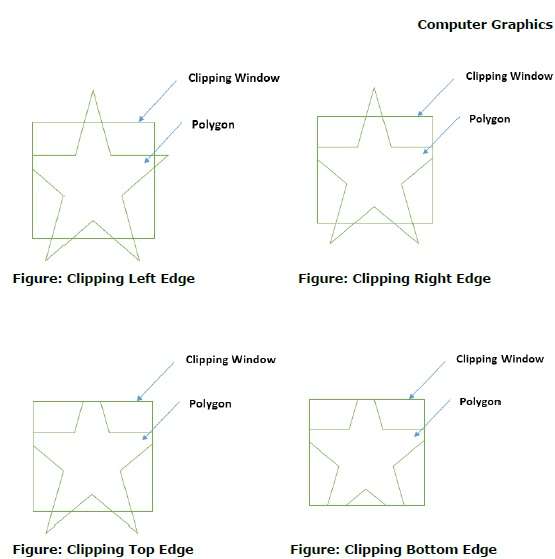
クリッピングウィンドウを使用してポリゴンのエッジを処理しているときに、エッジがクリッピングウィンドウの完全に内側になく、交点から外側のエッジまでの部分的なエッジがクリップされている場合、交点が検出されます。次の図は、左、右、上、下のエッジの切り抜きを示しています-

テキストクリッピング

コンピュータグラフィックスでテキストクリッピングを提供するために、さまざまな手法が使用されます。これは、文字の生成に使用される方法と特定のアプリケーションの要件によって異なります。以下にリストされているテキストクリッピングの3つの方法があります-

すべてまたはまったく文字列のクリッピング
すべてまたはまったく文字のクリッピング
テキストクリッピング

次の図は、文字列のクリッピングがすべてまたはまったくないことを示しています。

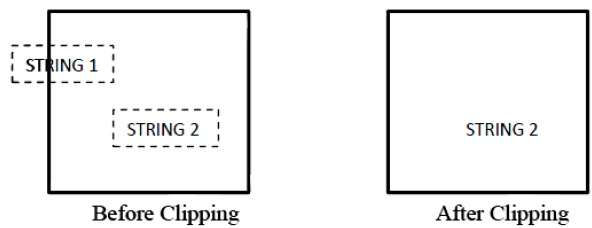
すべてまたはまったく文字列のクリッピング方法では、文字列全体を保持するか、クリッピングウィンドウに基づいて文字列全体を拒否します。上の図に示すように、STRING2は完全にクリッピングウィンドウ内にあるため、それを保持し、STRING1は部分的にのみウィンドウ内にあるため、拒否します。

次の図は、文字のクリッピングがすべてまたはまったくないことを示しています-

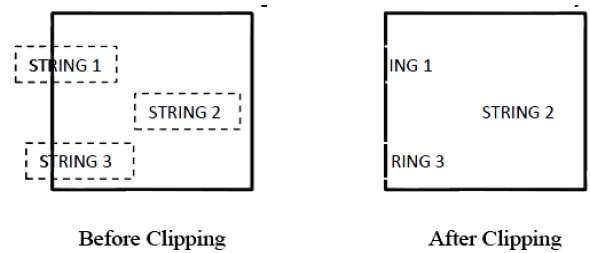
このクリッピング方法は、文字列全体ではなく文字に基づいています。この方法では、文字列が完全にクリッピングウィンドウ内にある場合、それを保持します。部分的にウィンドウの外側にある場合、-

文字列の外側にある部分のみを拒否します
文字がクリッピングウィンドウの境界にある場合、その文字全体を破棄し、残りの文字列を保持します。

次の図は、テキストのクリッピングを示しています-

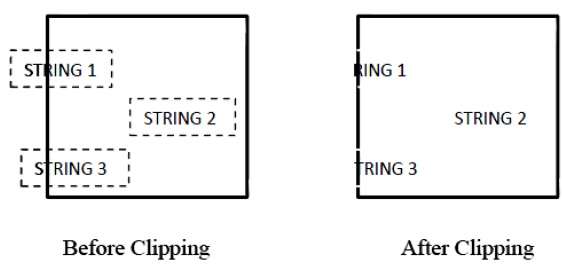
このクリッピング方法は、文字列全体ではなく文字に基づいています。この方法では、文字列が完全にクリッピングウィンドウ内にある場合、それを保持します。部分的に窓の外にある場合は、

文字列の外側にある部分のみを拒否します。
文字がクリッピングウィンドウの境界上にある場合、クリッピングウィンドウの外側にある文字の部分のみを破棄します。

ビットマップグラフィックス

ビットマップは、画像を説明するピクセルのコレクションです。これは、コンピューターが画像の保存と表示に使用するコンピューターグラフィックスの一種です。このタイプのグラフィックスでは、画像はビットごとに保存されるため、ビットマップグラフィックスと呼ばれます。理解を深めるために、ビットマップグラフィックを使用してスマイリーフェイスを描く次の例を考えてみましょう。

ここで、このスマイリーフェイスがコンピュータグラフィックスに少しずつ保存される様子を見ていきます。

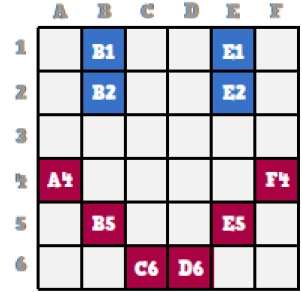
元のスマイリーフェイスをよく見ると、上の図ではB1、B2、E1、E2の2本の青い線があることがわかります。

同様に、スマイリーは、それぞれA4、B5、C6、D6、E5、およびF4の組み合わせビットを使用して表されます。

ビットマップグラフィックスの主な欠点は次のとおりです。

ビットマップ画像のサイズを変更することはできません。サイズを変更しようとすると、ピクセルがぼやけます。
色付きのビットマップは非常に大きくなる可能性があります。

変換とは、ルールを適用して一部のグラフィックを別のグラフィックに変更することを意味します。平行移動、スケールアップまたはスケールダウン、回転、せん断など、さまざまなタイプの変換を行うことができます。変換が2D平面で行われる場合、それは2D変換と呼ばれます。

変換は、コンピュータグラフィックスで重要な役割を果たし、画面上のグラフィックスの位置を変更し、サイズや向きを変更します。

同次座標

平行移動とそれに続く回転とスケーリングなどの一連の変換を実行するには、一連のプロセスに従う必要があります。

座標を変換し、
平行移動した座標を回転してから
回転した座標をスケーリングして、複合変換を完了します。

このプロセスを短縮するには、2×2変換行列の代わりに3×3変換行列を使用する必要があります。2×2行列を3×3行列に変換するには、ダミー座標Wを追加する必要があります。

このようにして、ポイントを2つの数字ではなく3つの数字で表すことができます。 Homogenous Coordinateシステム。このシステムでは、すべての変換方程式を行列乗算で表すことができます。任意のデカルト点P（X、Y）は、P '（X _h、Y _h、h）によって同次座標に変換できます。

翻訳

平行移動は、オブジェクトを画面上の別の位置に移動します。元の座標（X、Y）に平行移動座標（t _x、t _y）を追加して、新しい座標（X '、Y'）を取得することにより、2Dで点を平行移動できます。

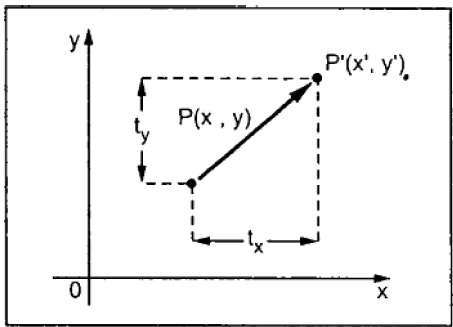
上の図から、次のように書くことができます-

X’ = X + t_x

Y’ = Y + t_y

ペア（t _x、t _y）は、平行移動ベクトルまたはシフトベクトルと呼ばれます。上記の方程式は、列ベクトルを使用して表すこともできます。

$P = \frac{[X]}{[Y]}$ p '= $\frac{[X']}{[Y']}$T = $\frac{[t_{x}]}{[t_{y}]}$

−と書くことができます

P’ = P + T

回転

回転では、オブジェクトを原点から特定の角度θ（シータ）で回転させます。次の図から、点P（X、Y）は、原点からの距離rで水平X座標から角度φに位置していることがわかります。

角度θで回転させたいとしましょう。それを新しい場所に回転させた後、新しい点P '（X'、Y '）を取得します。

標準の三角関数を使用すると、点P（X、Y）の元の座標は次のように表すことができます。

$X = r \, cos \, \phi ...... (1)$

$Y = r \, sin \, \phi ...... (2)$

同じように、点P '（X'、Y '）を-として表すことができます。

${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$

${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$

式（1）と（2）をそれぞれ（3）と（4）に代入すると、次のようになります。

${x}'= x \: cos \: \theta − \: y \: sin \: \theta $

${y}'= x \: sin \: \theta + \: y \: cos \: \theta $

上記の方程式を行列形式で表すと、

$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}OR $$

P '= P∙R

ここで、Rは回転行列です。

$$R = \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}$$

回転角は正と負のどちらでもかまいません。

正の回転角の場合、上記の回転行列を使用できます。ただし、負の回転角の場合、行列は次のように変化します-

$$R = \begin{bmatrix} cos(−\theta) & sin(−\theta) \\ -sin(−\theta) & cos(−\theta) \end{bmatrix}$$

$$=\begin{bmatrix} cos\theta & −sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(−\theta ) = cos \theta \; and\; sin(−\theta ) = −sin \theta \right )$$

スケーリング

オブジェクトのサイズを変更するには、スケーリング変換を使用します。スケーリングプロセスでは、オブジェクトの寸法を拡大または縮小します。スケーリングは、オブジェクトの元の座標にスケーリング係数を掛けて、目的の結果を得ることができます。

元の座標が（X、Y）、倍率が（S _X、S _Y）、生成された座標が（X '、Y'）であると仮定します。これは、以下に示すように数学的に表すことができます-

X' = X . S_X and Y' = Y . S_Y

スケーリングファクタS _X、S _YはそれぞれXおよびY方向にオブジェクトをスケーリングします。上記の方程式は、次のように行列形式で表すこともできます。

$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\\ 0 & S_{y} \end{bmatrix}$$

または

P’ = P . S

ここで、Sはスケーリング行列です。スケーリングプロセスを次の図に示します。

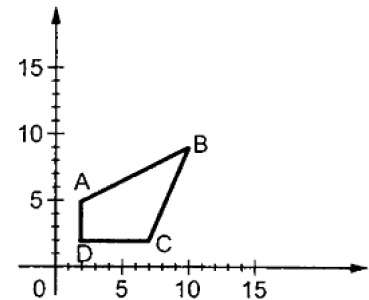
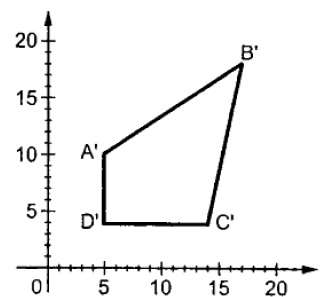
倍率Sに1未満の値を指定すると、オブジェクトのサイズを小さくすることができます。1より大きい値を指定すると、オブジェクトのサイズを大きくすることができます。

反射

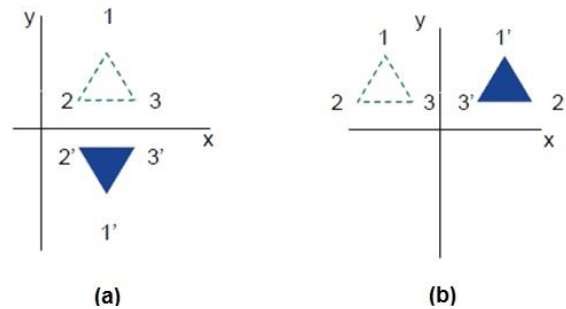
反射は、元のオブジェクトの鏡像です。つまり、180°の回転操作と言えます。反射変換では、オブジェクトのサイズは変更されません。

次の図は、X軸とY軸、および原点に関する反射をそれぞれ示しています。

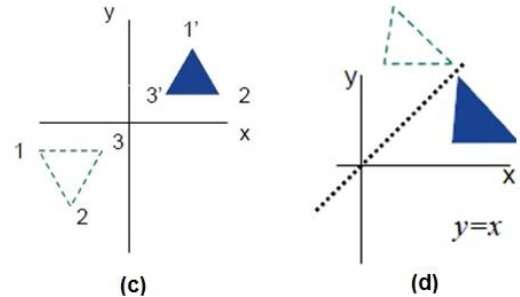
剪断

オブジェクトの形状を傾斜させる変換は、せん断変換と呼ばれます。2つのせん断変換がありますX-Shear そして Y-Shear。1つはX座標値をシフトし、もう1つはY座標値をシフトします。しかしながら; どちらの場合も、1つの座標のみがその座標を変更し、他の座標はその値を保持します。せん断は、Skewing。

X-Shear

X-ShearはY座標を保持し、X座標に変更が加えられます。これにより、下の図に示すように、垂直線が右または左に傾斜します。

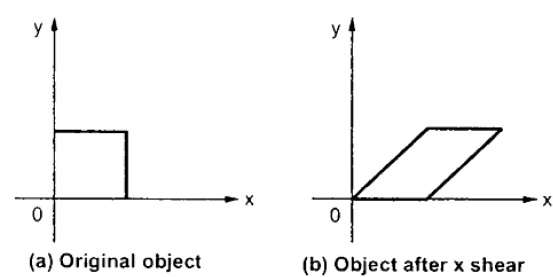
X-Shearの変換行列は、次のように表すことができます。

$$X_{sh} = \begin{bmatrix} 1& shx& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

Y」= Y + Shの_Y。バツ

X '= X

Yシアー

Yシアーは、X座標を保持し、Y座標を変更します。これにより、次の図に示すように、水平線が上下に傾斜する線に変換されます。

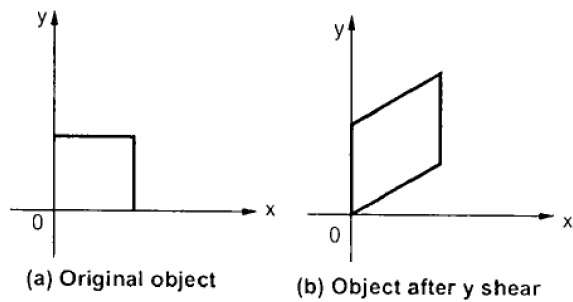
Yせん断は、次のように行列で表すことができます。

$$Y_{sh} \begin{bmatrix} 1& 0& 0\\ shy& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

X」= X +のSh _X。Y

Y '= Y

複合変換

平面Ｔ１の変換の後に第２の平面変換Ｔ２が続く場合、結果自体は、その順序で取られたＴ１およびＴ２の合成である単一の変換Ｔによって表され得る。これはT = T1∙T2と書かれています。

複合変換は、変換行列を連結して結合された変換行列を取得することで実現できます。

結合された行列-

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

ここで、[Ti]はの任意の組み合わせです

Translation
Scaling
Shearing
Rotation
Reflection

一般に行列の乗算は累積的ではないため、変換の順序を変更すると、結果が異なります。つまり、[A]です。[B]≠[B]。[A]と乗算の順序。変換を構成する基本的な目的は、一連の変換を次々に適用するのではなく、単一の構成された変換をポイントに適用することによって効率を上げることです。

たとえば、オブジェクトを任意の点（X _p、Y _p）を中心に回転させるには、次の3つの手順を実行する必要があります。

点（X _p、Y _p）を原点に移動します。
原点を中心に回転させます。
最後に、回転の中心を元の位置に戻します。

2Dシステムでは、2つの座標XとYのみを使用しますが、3Dでは、追加の座標Zが追加されます。3Dグラフィックス技術とそのアプリケーションは、エンターテインメント、ゲーム、およびコンピューター支援設計業界の基本です。これは、科学的可視化の継続的な研究分野です。

さらに、3Dグラフィックスコンポーネントは現在、ほぼすべてのパーソナルコンピュータの一部であり、従来はゲームなどのグラフィックスを多用するソフトウェアを対象としていましたが、他のアプリケーションで使用されることが増えています。

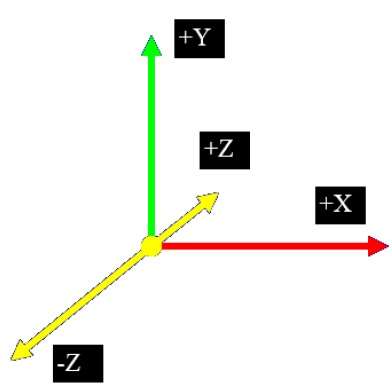
平行投影

平行投影はz座標を破棄し、オブジェクトの各頂点からの平行線は、ビュー平面と交差するまで延長されます。平行投影では、投影の中心ではなく、投影の方向を指定します。

平行投影では、投影の中心から投影面までの距離は無限大です。このタイプの投影では、元のオブジェクトの接続に対応する線分によって、投影された頂点を接続します。

平行投影はあまり現実的ではありませんが、正確な測定には適しています。このタイプの投影では、平行線は平行のままであり、角度は保持されません。さまざまなタイプの平行投影が次の階層に示されています。

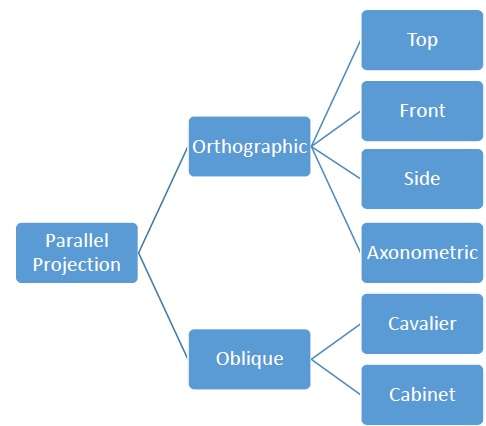
正射影

正射影では、射影の方向は平面の射影に垂直です。正射影には3つのタイプがあります-

フロントプロジェクション
トッププロジェクション
サイドプロジェクション

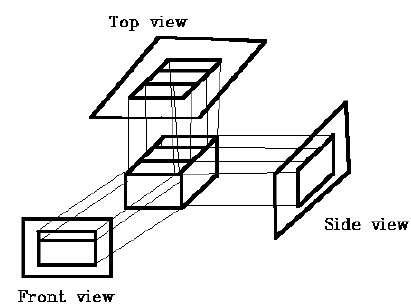
斜投影

斜投影では、投影の方向は平面の投影に垂直ではありません。斜投影では、正射影よりもオブジェクトをよく見ることができます。

斜投影には2つのタイプがあります- Cavalier そして Cabinet。キャバリエ投影は、投影面に対して45°の角度をなします。ビュー平面に垂直な線の投影は、キャバリエ投影の線自体と同じ長さです。キャバリアー投影では、3つの主方向すべての短縮係数は等しくなります。

キャビネットの投影は、投影面に対して63.4°の角度をなします。キャビネット投影では、表示面に垂直な線は実際の長さの1/2で投影されます。両方の予測を次の図に示します-

等角投影

オブジェクトの複数の側面を示す正射図法は、 axonometric orthographic projections。最も一般的な軸測投影法はisometric projectionここで、投影面はモデル座標系の各座標軸と等距離で交差します。この投影では、線の平行度は保持されますが、角度は保持されません。次の図は、等角投影を示しています-

透視投影

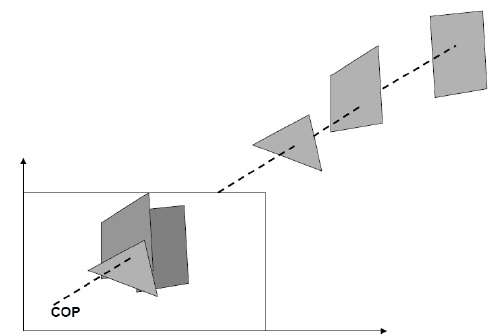
透視投影では、投影の中心から投影面までの距離は有限であり、オブジェクトのサイズは距離に反比例して変化し、よりリアルに見えます。

距離と角度は保持されず、平行線は平行のままではありません。代わりに、それらはすべて、と呼ばれる単一の点に収束しますcenter of projection または projection reference point。次のグラフに示す3種類の透視投影があります。

One point 透視投影は簡単に描くことができます。
Two point 透視投影は、奥行きの印象を良くします。
Three point 透視投影を描くのは最も難しいです。

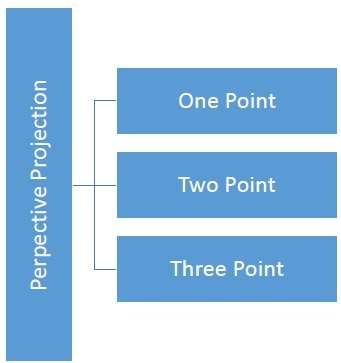
次の図は、3つのタイプの透視投影すべてを示しています-

翻訳

3D変換では、X座標とY座標とともにZ座標を転送します。3Dでの平行移動のプロセスは、2D平行移動に似ています。平行移動は、オブジェクトを画面上の別の位置に移動します。

次の図は、変換の効果を示しています-

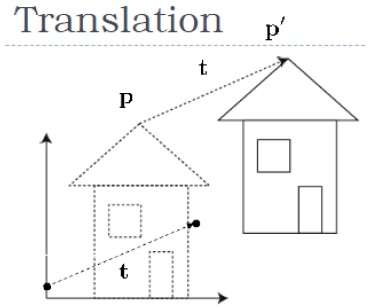
平行移動座標を追加することにより、ポイントを3Dで平行移動できます。 $(t_{x,} t_{y,} t_{z})$ 元の座標（X、Y、Z）に移動して、新しい座標（X '、Y'、Z '）を取得します。

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

P '= P∙T

$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$

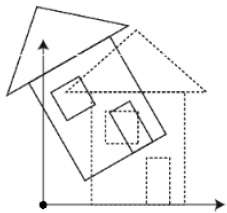
回転

3D回転は2D回転と同じではありません。3D回転では、回転軸とともに回転角を指定する必要があります。X、Y、Z軸を中心に3D回転を実行できます。それらは以下のようなマトリックス形式で表されます-

$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & −sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ −sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} cos\theta & −sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$

次の図は、さまざまな軸を中心とした回転を説明しています-

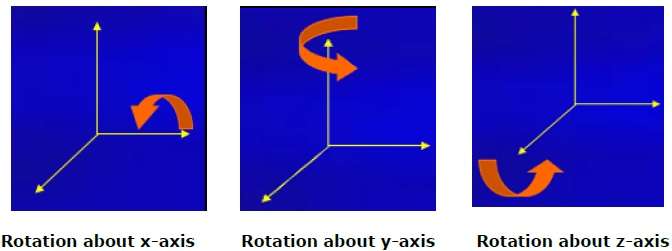
スケーリング

スケーリング変換を使用して、オブジェクトのサイズを変更できます。スケーリングプロセスでは、オブジェクトの寸法を拡大または縮小します。スケーリングは、オブジェクトの元の座標にスケーリング係数を掛けて、目的の結果を得ることができます。次の図は、3Dスケーリングの効果を示しています-

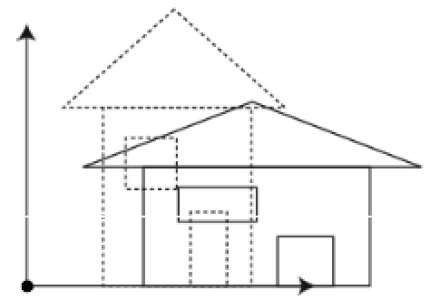
3Dスケーリング操作では、3つの座標が使用されます。元の座標が（X、Y、Z）であり、倍率が次のようになっていると仮定します。$(S_{X,} S_{Y,} S_{z})$それぞれ、生成される座標は（X '、Y'、Z '）です。これは、以下に示すように数学的に表すことができます-

$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

P '= P∙S

$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$

剪断

オブジェクトの形状を傾斜させる変換は、 shear transformation。2Dシアーと同様に、3DでX軸、Y軸、またはZ軸に沿ってオブジェクトをシアーすることができます。

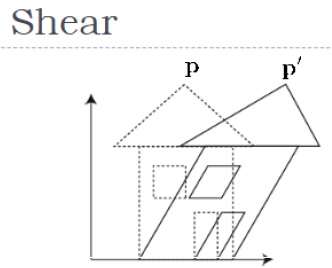
上の図に示すように、座標Pがあります。それをせん断して新しい座標P 'を取得できます。これは、次のように3D行列形式で表すことができます。

$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

P '= P∙Sh

$X’ = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z$

$Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z$

$Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z$

変換行列

変換行列は、変換の基本的なツールです。nxm次元の行列は、オブジェクトの座標で乗算されます。通常、変換には3 x3または4x4の行列が使用されます。たとえば、さまざまな操作について次の行列を考えてみます。

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$	$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$	$Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
Translation Matrix	Scaling Matrix	Shear Matrix
$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & -sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ -sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{z}(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
Rotation Matrix

コンピュータグラフィックスでは、さまざまな種類のオブジェクトを画面に描画する必要があることがよくあります。オブジェクトは常にフラットではないため、オブジェクトを描画するには何度も曲線を描画する必要があります。

曲線の種類

曲線は、無限に大きな点のセットです。各ポイントには、エンドポイントを除いて2つのネイバーがあります。曲線は大きく3つのカテゴリに分類できます-explicit, implicit, そして parametric curves。

陰曲線

暗黙の曲線表現は、曲線上の点が入っているかどうかをテストできる手順を使用して、曲線上の点のセットを定義します。通常、陰曲線は次の形式の陰関数によって定義されます。

f（x、y）= 0

複数値の曲線（x値に対して複数のy値）を表すことができます。一般的な例は円であり、その暗黙の表現は

x² + y² - R² = 0

明示的な曲線

数学関数y = f（x）を曲線としてプロットできます。このような関数は、曲線の明示的な表現です。明示的な表現は、垂直線を表すことができず、単一値でもあるため、一般的ではありません。xの値ごとに、通常、yの単一の値のみが関数によって計算されます。

パラメトリック曲線

パラメトリック形式の曲線は、パラメトリック曲線と呼ばれます。明示的および暗黙的な曲線表現は、関数がわかっている場合にのみ使用できます。実際には、パラメトリック曲線が使用されます。2次元のパラメトリック曲線は次の形式になります-

P（t）= f（t）、g（t）またはP（t）= x（t）、y（t）

関数fとgは、曲線上の任意の点の（x、y）座標になり、パラメーターtが特定の間隔[a、b]、通常は[0、1]にわたって変化したときに点が取得されます。

ベジェ曲線

ベジェ曲線はフランスのエンジニアによって発見されました Pierre Bézier。これらの曲線は、他のポイントの制御下で生成できます。制御点を使用した近似接線を使用して曲線を生成します。ベジェ曲線は数学的に次のように表すことができます-

$$\sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t)$$

どこ $p_{i}$ ポイントのセットであり、 ${B_{i}^{n}}(t)$ −で与えられるバーンスタイン多項式を表します

$${B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{n-i}t^{i}$$

どこ n は多項式の次数であり、 i はインデックスであり、 t は変数です。

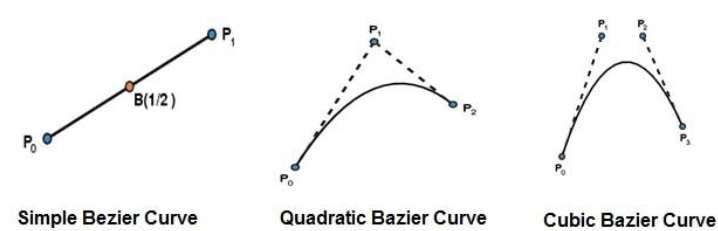
最も単純なベジエ曲線は、点からの直線です。 $P_{0}$ に $P_{1}$。二次ベジェ曲線は、3つの制御点によって決定されます。立方ベジェ曲線は、4つの制御点によって決定されます。

ベジェ曲線の特性

ベジェ曲線には次の特性があります-

これらは通常、コントロールポイントを結合するセグメントで構成されるコントロールポリゴンの形状に従います。
それらは常に最初と最後のコントロールポイントを通過します。
それらは、それらを定義する制御点の凸包に含まれています。
曲線セグメントを定義する多項式の次数は、定義するポリゴンポイントの数より1つ少なくなります。したがって、4つの制御点の場合、多項式の次数は3、つまり3次多項式です。
ベジェ曲線は通常、定義するポリゴンの形状に従います。
終点での接線ベクトルの方向は、最初と最後のセグメントによって決定されるベクトルの方向と同じです。
ベジェ曲線の凸包特性により、多項式が制御点にスムーズに従うことが保証されます。
制御ポリゴンと交差する回数よりも多くの回数、ベジェ曲線と交差する直線はありません。
それらはアフィン変換の下では不変です。
ベジェ曲線はグローバル制御を示します。つまり、制御点を移動すると曲線全体の形状が変化します。
与えられたベジェ曲線は、点t = t0で、パラメータ値t = t0に対応する点で結合する2つのベジェセグメントに分割できます。

Bスプライン曲線

バーンスタイン基底関数によって生成されるベジェ曲線の柔軟性は限られています。

まず、指定されたポリゴン頂点の数によって、曲線を定義する結果の多項式の順序が固定されます。
2番目の制限特性は、曲線全体のすべてのパラメーター値でブレンディング関数の値がゼロ以外になることです。

Bスプライン基底には、特殊なケースとしてバーンスタイン基底が含まれています。Bスプラインベースは非グローバルです。

Bスプライン曲線は、制御点PiとBスプライン基底関数の線形結合として定義されます。 $N_{i,}$ k（t）によって与えられる

$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \: [ tk-1,tn+1 ]$

どこ、

{{$p_{i}$：i = 0、1、2….n}はコントロールポイントです
kは、Bスプライン曲線の多項式セグメントの次数です。次数kは、曲線が次数k-1の区分的多項式セグメントで構成されていることを意味します。
インクルード $N_{i,k}(t)$「正規化されたBスプラインブレンディング関数」です。それらは、次数kと、通常「ノットシーケンス」と呼ばれる実数の減少しないシーケンスによって記述されます。

$${t_{i}:i = 0, ... n + K}$$

N _i、k関数は次のように記述されます-

$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0,& Otherwise \end{matrix}\right.$$

k> 1の場合、

$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}} N_{i,k-1}(t) + \frac{t_{i+k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$

そして

$$t \: \epsilon \: [t_{k-1},t_{n+1})$$

Bスプライン曲線の特性

Bスプライン曲線には次の特性があります-

任意のパラメーター値のBスプライン基底関数の合計は1です。
各基底関数は、すべてのパラメーター値に対して正またはゼロです。
k = 1を除いて、各基底関数には正確に1つの最大値があります。
曲線の最大次数は、ポリゴンを定義する頂点の数と同じです。
Bスプライン多項式の次数は、ポリゴンを定義する頂点の数に依存しません。
Bスプラインを使用すると、各頂点が、関連する基底関数がゼロ以外のパラメータ値の範囲でのみ曲線の形状に影響を与えるため、曲線サーフェスをローカルで制御できます。
曲線は、変動を減少させる特性を示しています。
曲線は通常、ポリゴンを定義する形状に従います。
ポリゴンを定義する頂点にアフィン変換を適用することにより、任意のアフィン変換を曲線に適用できます。
定義するポリゴンの凸包内の曲線。

ポリゴンサーフェス

オブジェクトは、サーフェスのコレクションとして表されます。3Dオブジェクト表現は2つのカテゴリに分けられます。

Boundary Representations (B-reps) − 3Dオブジェクトを、オブジェクトの内部を環境から分離する一連のサーフェスとして記述します。
Space–partitioning representations −オブジェクトを含む空間領域を、重なり合わない小さな連続したソリッド（通常は立方体）のセットに分割することにより、内部プロパティを記述するために使用されます。

3Dグラフィックスオブジェクトで最も一般的に使用される境界表現は、オブジェクトの内部を囲むサーフェスポリゴンのセットです。多くのグラフィックシステムはこの方法を使用します。ポリゴンのセットは、オブジェクトの説明のために保存されます。これにより、すべてのサーフェスを線形方程式で記述できるため、オブジェクトのサーフェスレンダリングと表示が簡素化および高速化されます。

ポリゴンサーフェスは、設計およびソリッドモデリングアプリケーションで一般的です。 wireframe display表面構造の一般的な指標を与えるために迅速に行うことができます。次に、ポリゴンサーフェス全体のシェーディングパターンを補間して照らすことにより、リアルなシーンが生成されます。

ポリゴンテーブル

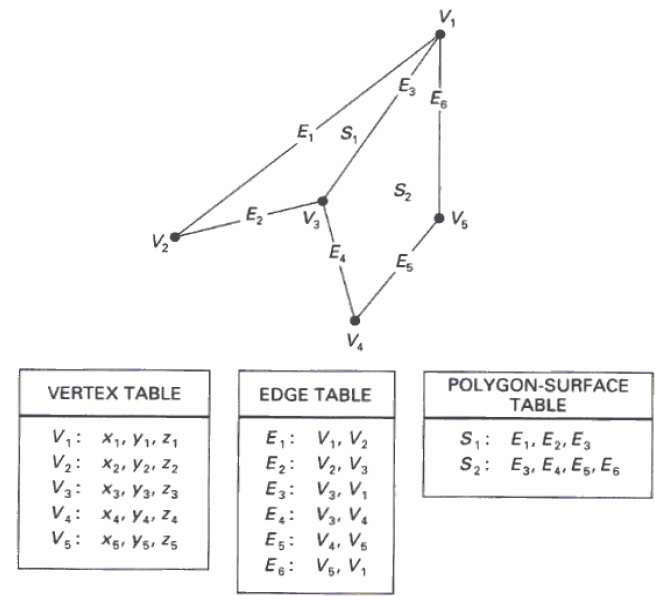
この方法では、サーフェスは頂点座標と関連する属性のセットによって指定されます。次の図に示すように、5つの頂点は、Vから、ある₁からV ₅。

各頂点には、テーブルにv ₁：x ₁、y ₁、z ₁として表されるx、y、およびz座標情報が格納されます。
Edgeテーブルは、ポリゴンのエッジ情報を格納するために使用されます。以下の図において、エッジE ₁頂点vとの間にある₁及びV ₂ Eとして表に示されている₁：V ₁、V ₂。
ポリゴンサーフェステーブルには、ポリゴンに存在するサーフェスの数が格納されます。以下の図から、表面S _1は、エッジEによって覆われている₁、E ₂およびE ₃ Sとしてのポリゴン面テーブルで表現することができる₁ E：₁、E ₂、及びE ₃。

平面方程式

平面の方程式は次のように表すことができます。

Ax + By + Cz + D = 0

ここで、（x、y、z）は平面上の任意の点であり、係数A、B、C、およびDは平面の空間プロパティを表す定数です。A、B、C、およびDの値は、平面内の3つの非同一線上の点の座標値を使用して3つの平面方程式のセットを解くことによって取得できます。平面の3つの頂点が（x ₁、y ₁、z ₁）、（x ₂、y ₂、z ₂）および（x ₃、y ₃、z ₃）であると仮定します。

比率A / D、B / D、およびC / Dについて次の連立方程式を解きます。A、B、C、およびDの値を取得します。

（A / D）x ₁ +（B / D）y ₁ +（C / D）z ₁ = -1

（A / D）x ₂ +（B / D）y ₂ +（C / D）z ₂ = -1

（A / D）x ₃ +（B / D）y ₃ +（C / D）z ₃ = -1

上記の方程式を行列式で取得するには、クラメルの法則を上記の方程式に適用します。

$A = \begin{bmatrix} 1& y_{1}& z_{1}\\ 1& y_{2}& z_{2}\\ 1& y_{3}& z_{3} \end{bmatrix} B = \begin{bmatrix} x_{1}& 1& z_{1}\\ x_{2}& 1& z_{2}\\ x_{3}& 1& z_{3} \end{bmatrix} C = \begin{bmatrix} x_{1}& y_{1}& 1\\ x_{2}& y_{2}& 1\\ x_{3}& y_{3}& 1 \end{bmatrix} D = - \begin{bmatrix} x_{1}& y_{1}& z_{1}\\ x_{2}& y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}$

パラメータA、B、C、およびDを持つ任意の点（x、y、z）について、次のように言うことができます。

Ax + By + Cz + D≠0は、点が平面上にないことを意味します。
Ax + By + Cz + D <0は、ポイントがサーフェスの内側にあることを意味します。
Ax + By + Cz + D> 0は、ポイントがサーフェスの外側にあることを意味します。

ポリゴンメッシュ

3Dサーフェスとソリッドは、ポリゴン要素とライン要素のセットで近似できます。そのような表面は呼ばれますpolygonal meshes。ポリゴンメッシュでは、各エッジは最大2つのポリゴンで共有されます。ポリゴンまたは面のセットは、一緒になってオブジェクトの「スキン」を形成します。

このメソッドは、グラフィックスで幅広いクラスのソリッド/サーフェスを表すために使用できます。ポリゴンメッシュは、隠面判定アルゴリズムを使用してレンダリングできます。ポリゴンメッシュは3つの方法で表すことができます-

明示的な表現
頂点リストへのポインタ
エッジリストへのポインタ

利点

ほぼすべてのオブジェクトのモデル化に使用できます。
それらは、頂点のコレクションとして簡単に表すことができます。
それらは簡単に変形できます。
それらはコンピュータ画面上で簡単に描くことができます。

短所

曲面はおおよその説明しかできません。
髪の毛や液体など、ある種のオブジェクトをシミュレートすることは困難です。

不透明なオブジェクトや表面を含む画像を表示する場合、目の近くのオブジェクトから後ろにあるオブジェクトをビューから見ることはできません。リアルな画面イメージを得るには、これらの隠れた表面を削除する必要があります。これらの表面の識別と除去は、Hidden-surface problem。

隠面問題を取り除くには2つのアプローチがあります- Object-Space method そして Image-space method。オブジェクト空間法は物理座標系で実装され、画像空間法は画面座標系で実装されます。

2D画面に3Dオブジェクトを表示する場合は、選択した表示位置から見える画面の部分を特定する必要があります。

デプスバッファ（Zバッファ）方式

このメソッドはCutmullによって開発されました。これは画像空間アプローチです。基本的な考え方は、各サーフェスのZ深度をテストして、最も近い（可視の）サーフェスを決定することです。

この方法では、各サーフェスは、サーフェス全体で一度に1ピクセル位置ずつ個別に処理されます。ピクセルの深度値が比較され、最も近い（最小のz）サーフェスがフレームバッファーに表示される色を決定します。

ポリゴンの表面に非常に効率的に適用されます。サーフェスは任意の順序で処理できます。遠いポリゴンから近いポリゴンをオーバーライドするために、frame buffer そして depth buffer, 使用されています。

Depth buffer サーフェスが処理されるときに（x、y）位置の深度値を格納するために使用されます（0≤深度≤1）。

ザ・ frame buffer 各位置（x、y）での色値の強度値を格納するために使用されます。

z座標は通常、範囲[0、1]に正規化されます。z座標の0の値は背面のクリッピングペインを示し、z座標の1の値は前面のクリッピングペインを示します。

アルゴリズム

Step-1 −バッファ値を設定します−

デプスバッファー（x、y）= 0

フレームバッファ（x、y）=背景色

Step-2 −各ポリゴンを処理します（一度に1つずつ）

ポリゴンの投影された（x、y）ピクセル位置ごとに、深さzを計算します。

Z>深度バッファ（x、y）の場合

表面の色を計算し、

デプスバッファー（x、y）= z、

フレームバッファ（x、y）=表面色（x、y）

利点

実装は簡単です。
ハードウェアに実装すると、速度の問題が軽減されます。
一度に1つのオブジェクトを処理します。

短所

大容量のメモリが必要です。
それは時間のかかるプロセスです。

スキャンライン方式

これは、目に見える表面を識別するための画像空間法です。このメソッドには、単一のスキャンラインのみの深度情報があります。深度値の1つのスキャンラインを必要とするために、次のスキャンラインを処理する前に、特定のスキャンラインと交差するすべてのポリゴンを同時にグループ化して処理する必要があります。2つの重要なテーブル、edge table そして polygon table, このために維持されます。

The Edge Table −シーン内の各ラインの座標エンドポイント、各ラインの逆勾配、およびエッジをサーフェスに接続するためのポリゴンテーブルへのポインタが含まれています。

The Polygon Table −平面係数、表面材料特性、その他の表面データが含まれており、エッジテーブルへのポインタである可能性があります。

特定のスキャンラインを横切るサーフェスの検索を容易にするために、エッジのアクティブなリストが形成されます。アクティブリストには、xの昇順でスキャンラインと交差するエッジのみが保存されます。また、各サーフェスにフラグが設定され、スキャンラインに沿った位置がサーフェスの内側にあるか外側にあるかを示します。

各スキャンライン全体のピクセル位置は、左から右に処理されます。サーフェスとの左側の交差点ではサーフェスフラグがオンになり、右側ではフラグがオフになります。複数のサーフェスのフラグが特定のスキャンライン位置でオンになっている場合にのみ、深度計算を実行する必要があります。

面積分割法

エリアサブディビジョン方式は、単一のサーフェスの一部を表すビューエリアを配置することで利用できます。各小さな領域が単一の可視表面の一部の投影になるか、表面がまったくなくなるまで、表示領域全体をますます小さな長方形に分割します。

サブディビジョンが単一のサーフェスに属するものとして簡単に分析されるまで、またはサブディビジョンが単一のピクセルのサイズに縮小されるまで、このプロセスを続けます。これを行う簡単な方法は、各ステップで領域を4つの等しい部分に連続的に分割することです。サーフェスが指定された領域境界と持つことができる4つの可能な関係があります。

Surrounding surface −エリアを完全に囲むもの。
Overlapping surface −一部がエリア内にあり一部がエリア外にあるもの。
Inside surface −完全にエリア内にあるもの。
Outside surface −完全にエリア外にあるもの。

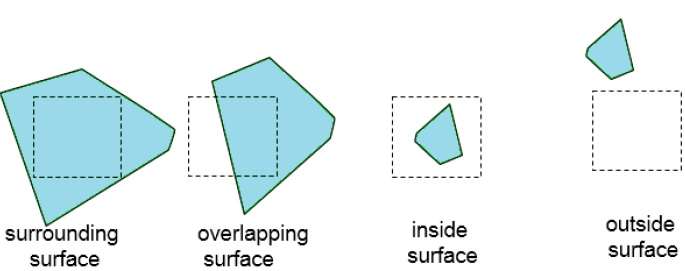
エリア内の表面の可視性を決定するためのテストは、これらの4つの分類の観点から述べることができます。次の条件のいずれかが当てはまる場合、指定された領域をさらに細分化する必要はありません。

すべてのサーフェスは、領域に対して外側のサーフェスです。
この領域には、内側、重なり合う、または周囲の表面が1つだけあります。
周囲のサーフェスは、エリア境界内の他のすべてのサーフェスを覆い隠します。

裏面検出

多面体の背面を識別するための高速で単純なオブジェクト空間の方法は、「内外」テストに基づいています。点（x、y、z）は、平面パラメータA、B、C、およびDを持つポリゴンサーフェスの「内側」にあります。内側のポイントがサーフェスの視線に沿っている場合、ポリゴンは背面（私たちはその顔の内側にいて、私たちの表示位置からはその正面を見ることができません）。

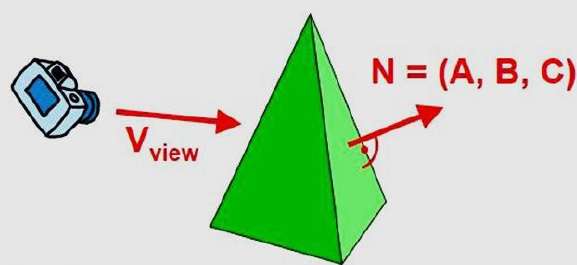
法線ベクトルを考慮することにより、このテストを簡略化できます。 N デカルト成分（A、B、C）を持つポリゴンサーフェスに。

一般に、Vが目（または「カメラ」）の位置からの視線方向のベクトルである場合、このポリゴンは次の場合に背面になります。

V.N > 0

さらに、オブジェクトの説明が投影座標に変換され、表示方向が表示のz軸に平行である場合、-

V =（0、0、V _z）および V.N = V _Z C

したがって、Cの符号を法線ベクトルの成分と見なすだけで済みます。 N。

ネガに沿った視線方向を持つ右利きの視界システム $Z_{V}$軸では、C <0の場合、ポリゴンは背面になります。また、視線方向がポリゴンに向かっているため、法線のz成分がC = 0の面は表示されません。したがって、一般に、法線ベクトルのaz成分値が-である場合、任意のポリゴンを背面としてラベル付けできます。

C <= 0

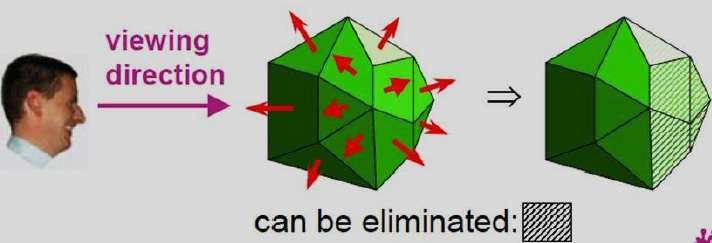
同様の方法は、左利きの表示システムを採用するパッケージでも使用できます。これらのパッケージでは、平面パラメータA、B、C、およびDは、時計回りの方向に指定されたポリゴンの頂点座標から計算できます（右回りのシステムで使用される反時計回りの方向とは異なります）。

また、背面には、表示位置から離れる方向を指す法線ベクトルがあり、表示方向が正に沿っている場合、C> = 0で識別されます。 $Z_{v}$軸。オブジェクトを定義するさまざまな平面のパラメータCを調べることにより、すべての背面をすぐに識別できます。

A-バッファ方式

Aバッファ方式は、深度バッファ方式の拡張です。Aバッファ方式は、ルーカスフィルムスタジオでレンダリングシステムRenders Everything You Ever Saw（REYES）用に開発された可視性検出方式です。

Aバッファは、透明度を許可するために深度バッファ方式を拡張します。Aバッファの重要なデータ構造は累積バッファです。

Aバッファの各位置には2つのフィールドがあります-

Depth field −正または負の実数を格納します
Intensity field −表面強度情報またはポインタ値を保存します

深さ> = 0の場合、その位置に格納される数値は、対応するピクセル領域と重なる単一のサーフェスの深さです。次に、強度フィールドには、そのポイントでの表面色のRGBコンポーネントとピクセルカバレッジのパーセントが格納されます。

深さが0未満の場合、ピクセル強度に対する複数の表面の寄与を示します。次に、強度フィールドには、サーフェスデータのリンクリストへのポインタが格納されます。Aバッファの表面バッファには次のものが含まれます。

RGB強度成分
不透明度パラメータ
Depth
エリアカバレッジのパーセント
表面識別子

アルゴリズムは、深度バッファアルゴリズムと同じように進行します。深度と不透明度の値は、ピクセルの最終的な色を決定するために使用されます。

深度ソート方法

深さの並べ替え方法は、画像空間とオブジェクト空間の両方の操作を使用します。深度ソート方法は、2つの基本的な機能を実行します-

まず、サーフェスは深さの降順で並べ替えられます。
次に、最も深い表面から始めて、表面が順番にスキャン変換されます。

ポリゴンサーフェスのスキャン変換は、画像空間で実行されます。隠面問題を解決するためのこの方法は、しばしばpainter's algorithm。次の図は、深度ソートの効果を示しています-

アルゴリズムは、深さで並べ替えることから始まります。たとえば、ポリゴンの初期の「深さ」の推定値は、ポリゴンの任意の頂点の最も近いz値であると見なすことができます。

リストの最後にあるポリゴンPを見てみましょう。zエクステントがPとオーバーラップするすべてのポリゴンQを考えます。Pを描く前に、次のテストを行います。次のテストのいずれかが陽性の場合、Qの前にPを引くことができると想定できます。

xエクステントは重複していませんか？
yエクステントは重複していませんか？
Pは完全にQの平面の反対側にありますか？
Qは完全にPの平面の視点と同じ側にありますか？
ポリゴンの投影は重なりませんか？

すべてのテストが失敗した場合、もう一方の平面を使用してPまたはQのいずれかを分割します。新しいカットポリゴンが深度オーダーに挿入され、プロセスが続行されます。理論的には、この分割によりO（n ²）個のポリゴンが生成される可能性がありますが、実際には、ポリゴンの数ははるかに少なくなります。

バイナリ空間分割（BSP）ツリー

バイナリ空間分割は、可視性を計算するために使用されます。BSPツリーを構築するには、ポリゴンから始めて、すべてのエッジにラベルを付ける必要があります。一度に1つのエッジのみを処理する場合は、各エッジを延長して、平面を2つに分割します。ツリーの最初のエッジをルートとして配置します。内側か外側かに基づいて、後続のエッジを追加します。すでにツリーにあるエッジの延長にまたがるエッジは2つに分割され、両方がツリーに追加されます。

上の図から、最初に A ルートとして。
図（a）のすべてのノードのリストを作成します。
ルートの前にあるすべてのノードを配置します A ノードの左側に A ルートの後ろにあるすべてのノードを配置します A 図（b）に示すように右側に。
最初にすべてのフロントノードを処理し、次にバックのノードを処理します。
図（c）に示すように、最初にノードを処理します B。ノードの前には何もないのでB、NILを入れました。ただし、ノードがありますC ノードの後ろに B、soノード C ノードの右側に移動します B。
ノードに対して同じプロセスを繰り返します D。

フランス系アメリカ人の数学者ブノワ・マンデルブロ博士がフラクタルを発見しました。ワードフラクタルは、ラテン語から派生したフラクタス手段が壊れました。

フラクタルとは何ですか？

フラクタルは、単一の数式からコンピューターによって生成された非常に複雑な画像です。それらは反復を使用して作成されます。これは、前の反復の結果を考慮して、わずかに異なる値で1つの数式が何度も繰り返されることを意味します。

フラクタルは、次のような多くの分野で使用されています。

Astronomy −銀河、土星の環などの分析に。
Biology/Chemistry −細菌の培養、化学反応、人体解剖学、分子、植物、
Others −雲、海岸線と境界線、データ圧縮、拡散、経済、フラクタルアート、フラクタル音楽、風景、特殊効果などを描写するため。

フラクタルの生成

次の図に示すように、同じ形状を何度も繰り返すことでフラクタルを生成できます。図（a）は正三角形を示しています。図（b）では、三角形が繰り返されて星のような形になっていることがわかります。図（c）では、図（b）の星の形が何度も繰り返されて新しい形が作られていることがわかります。

無制限の反復回数を実行して、目的の形状を作成できます。プログラミング用語では、再帰はそのような形状を作成するために使用されます。

幾何学的フラクタル

幾何学的フラクタルは、非整数またはフラクタル次元を持つ自然界に見られる形状を扱います。決定論的（非ランダム）自己相似フラクタルを幾何学的に構築するには、次のように呼ばれる特定の幾何学的形状から始めます。initiator。次に、イニシエーターのサブパーツは、と呼ばれるパターンに置き換えられます。generator。

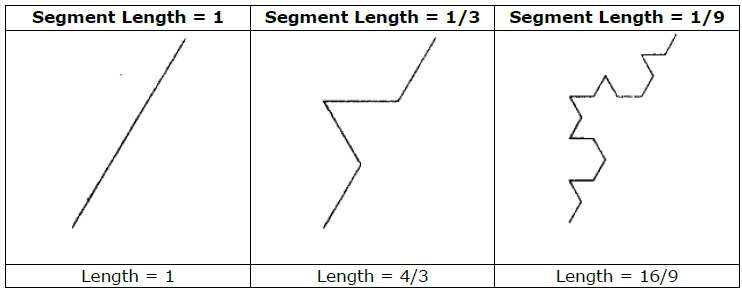
例として、上図に示すイニシエーターとジェネレーターを使用すると、それを繰り返すことで適切なパターンを構築できます。イニシエーターの各直線セグメントは、各ステップで4つの等しい長さの線分に置き換えられます。倍率は1/3であるため、フラクタル次元はD = ln 4 /ln3≈1.2619です。

また、イニシエーターの各線分の長さは、各ステップで4/3倍に増加するため、次の図に示すように、曲線に詳細が追加されると、フラクタル曲線の長さは無限大になる傾向があります。

アニメーションとは、コンピュータグラフィックスのあらゆるオブジェクトに生命を与えることを意味します。それは、一見無生物のように見える物体にエネルギーと感情を注入する力を持っています。コンピューター支援アニメーションとコンピューター生成アニメーションは、コンピューターアニメーションの2つのカテゴリです。それはフィルムまたはビデオを介して提示することができます。

アニメーションの背後にある基本的な考え方は、記録された画像を、人間の目をだまして連続的な動きとして解釈するのに十分な速度で再生することです。アニメーションは、一連の死んだ画像を生き生きとさせることができます。アニメーションは、エンターテインメント、コンピューター支援設計、科学的視覚化、トレーニング、教育、eコマース、コンピューターアートなどの多くの分野で使用できます。

アニメーションテクニック

アニメーターは、さまざまなアニメーション手法を発明して使用してきました。基本的に、このセクションで1つずつ説明する6つのアニメーション技法があります。

伝統的なアニメーション（フレームごと）

伝統的に、アニメーションのほとんどは手作業で行われました。アニメーションのすべてのフレームは手作業で描画する必要がありました。アニメーションの1秒あたり24フレーム（フィルム）が必要なため、最短のムービーでも作成するのに必要な労力は膨大なものになる可能性があります。

キーフレーミング

この手法では、ストーリーボードを配置してから、アーティストがアニメーションの主要なフレームを描画します。メジャーフレームは、顕著な変化が発生するフレームです。それらはアニメーションの要点です。キーフレーミングでは、アニメーターがオブジェクトのクリティカル位置またはキー位置を指定する必要があります。次に、コンピューターは、これらの位置の間をスムーズに補間することにより、欠落しているフレームを自動的に埋めます。

手続き

手続き型アニメーションでは、オブジェクトはキーフレームではなく、プロシージャ（一連のルール）によってアニメーション化されます。アニメーターはルールと初期条件を指定し、シミュレーションを実行します。ルールは、多くの場合、数式で表される実世界の物理的なルールに基づいています。

行動

行動アニメーションでは、自律的なキャラクターが、少なくともある程度は、自身の行動を決定します。これにより、キャラクターは即興で演奏できるようになり、アニメーターはすべてのキャラクターの動きの詳細を指定する必要がなくなります。

パフォーマンスベース（モーションキャプチャ）

もう1つの手法はモーションキャプチャです。モーションキャプチャでは、磁気または視覚ベースのセンサーが人間または動物の物体の動作を3次元で記録します。次に、コンピューターはこれらのデータを使用してオブジェクトをアニメーション化します。

このテクノロジーにより、多くの有名なアスリートがスポーツビデオゲームのキャラクターにアクションを提供できるようになりました。モーションキャプチャは、主に一般的な人間の行動の一部を比較的簡単にキャプチャできるため、アニメーターに非常に人気があります。ただし、被写体の形状や寸法とグラフィック文字の間に深刻な不一致がある可能性があり、これは正確な実行の問題につながる可能性があります。

物理ベース（ダイナミクス）

キーフレーミングや動画とは異なり、シミュレーションでは物理法則を使用して画像やその他のオブジェクトのモーションを生成します。シミュレーションは、物理的なリアリズムを維持しながら、わずかに異なるシーケンスを生成するために簡単に使用できます。第二に、リアルタイムシミュレーションは、実際の人がシミュレートされたキャラクターのアクションを操作できる、より高度な対話性を可能にします。

対照的に、キーフレーミングとモーション選択および変更モーションに基づくアプリケーションは、事前に計算されたモーションのライブラリを形成します。シミュレーションが苦しむ1つの欠点は、適切な制御システムを手作りするために必要な専門知識と時間です。

キーフレーミング

キーフレームは、アニメーションの変更を定義するフレームです。フレームごとのアニメーションを作成する場合、すべてのフレームがキーフレームです。誰かがコンピュータで3Dアニメーションを作成するとき、彼らは通常、すべての単一フレーム上の特定のオブジェクトの正確な位置を指定しません。キーフレームを作成します。

キーフレームは、オブジェクトがそのサイズ、方向、形状、またはその他のプロパティを変更する際の重要なフレームです。次に、コンピューターはその間のすべてのフレームを把握し、アニメーターの時間を大幅に節約します。次の図は、ユーザーが描画したフレームとコンピューターが生成したフレームを示しています。