コンピュータグラフィックスフラクタル

フランス系アメリカ人の数学者ブノワ・マンデルブロ博士がフラクタルを発見しました。ワードフラクタルは、ラテン語から派生したフラクタス手段が壊れました。

フラクタルとは何ですか？

フラクタルは、単一の数式からコンピューターによって生成された非常に複雑な画像です。それらは反復を使用して作成されます。これは、前の反復の結果を考慮して、わずかに異なる値で1つの数式が何度も繰り返されることを意味します。

フラクタルは、次のような多くの分野で使用されています。

Astronomy −銀河、土星の環などの分析に。
Biology/Chemistry −細菌の培養、化学反応、人体解剖学、分子、植物、
Others −雲、海岸線と境界線、データ圧縮、拡散、経済、フラクタルアート、フラクタル音楽、風景、特殊効果などを描写するため。

フラクタルの生成

次の図に示すように、同じ形状を何度も繰り返すことでフラクタルを生成できます。図（a）は正三角形を示しています。図（b）では、三角形が繰り返されて星のような形になっていることがわかります。図（c）では、図（b）の星の形が何度も繰り返されて新しい形が作られていることがわかります。

無制限の反復回数を実行して、目的の形状を作成できます。プログラミング用語では、再帰はそのような形状を作成するために使用されます。

幾何学的フラクタル

幾何学的フラクタルは、非整数またはフラクタル次元を持つ自然界に見られる形状を扱います。決定論的（非ランダム）自己相似フラクタルを幾何学的に構築するには、次のように呼ばれる特定の幾何学的形状から始めます。initiator。次に、イニシエーターのサブパーツは、と呼ばれるパターンに置き換えられます。generator。

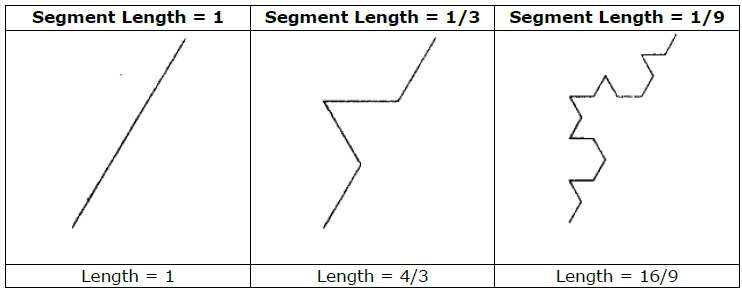
例として、上図に示すイニシエーターとジェネレーターを使用すると、それを繰り返すことで適切なパターンを構築できます。イニシエーターの各直線セグメントは、各ステップで4つの等しい長さの線分に置き換えられます。倍率は1/3であるため、フラクタル次元はD = ln 4 /ln3≈1.2619です。

また、イニシエーターの各線分の長さは、各ステップで4/3倍に増加するため、次の図に示すように、曲線に詳細が追加されると、フラクタル曲線の長さは無限大になる傾向があります。