円生成アルゴリズム

画面に円を描くことは、線を描くことよりも少し複雑です。円を生成するための2つの一般的なアルゴリズムがあります-Bresenham’s Algorithm そして Midpoint Circle Algorithm。これらのアルゴリズムは、円を描くために必要な後続のポイントを決定するという考えに基づいています。アルゴリズムについて詳しく説明しましょう-

円の方程式は$ X ^ {2} + Y ^ {2} = r ^ {2}、$です。ここで、rは半径です。

ブレゼンハムのアルゴリズム

ラスター表示で連続円弧を表示することはできません。代わりに、アークを完成させるために最も近いピクセル位置を選択する必要があります。

次の図から、ピクセルを（X、Y）の位置に配置し、次のピクセルを配置する場所を決定する必要があることがわかります-N（X + 1、Y）またはS（X + 1、 Y-1）。

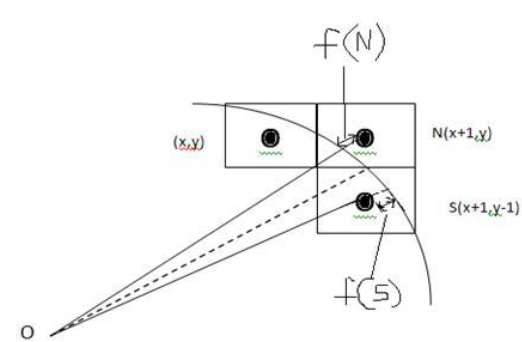
これは決定パラメータによって決定できます d。

d <= 0の場合、次のピクセルとしてN（X + 1、Y）が選択されます。
d> 0の場合、S（X + 1、Y-1）が次のピクセルとして選択されます。

アルゴリズム

Step 1−円の中心と半径の座標を取得し、それぞれx、y、Rに格納します。P = 0およびQ = Rに設定します。

Step 2 −決定パラメータD = 3 –2Rを設定します。

Step 3 −P≤Qの間、ステップ8を繰り返します。

Step 4 − Draw Circle（X、Y、P、Q）を呼び出します。

Step 5 −Pの値をインクリメントします。

Step 6 − D <0の場合、D = D + 4P +6。

Step 7 −その他のセットR = R -1、D = D + 4（PQ）+10。

Step 8 − Draw Circle（X、Y、P、Q）を呼び出します。

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

ミッドポイントアルゴリズム

Step 1 −入力半径 r 円の中心$（x_ {c、} y_ {c}）$を使用して、原点を中心とする円の円周上の最初の点を次のように取得します。

(x₀, y₀) = (0, r)

Step 2 −決定パラメータの初期値を次のように計算します。

$ P_ {0} $ = 5/4 – r（この式の簡略化については、次の説明を参照してください。）

f(x, y) = x² + y² - r² = 0

f(x_i - 1/2 + e, y_i + 1)
        = (x_i - 1/2 + e)² + (y_i + 1)² - r² 
        = (x_i- 1/2)² + (y_i + 1)² - r² + 2(x_i - 1/2)e + e²
        = f(x_i - 1/2, y_i + 1) + 2(x_i - 1/2)e + e² = 0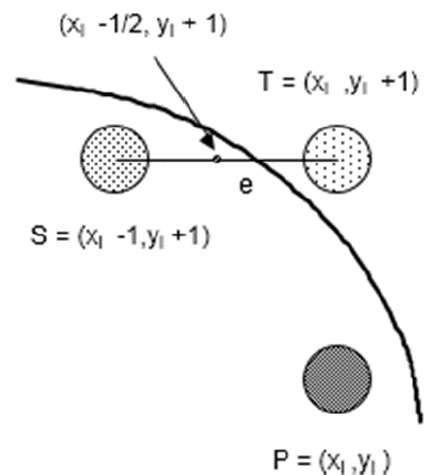

Let d_i = f(x_i - 1/2, y_i + 1) = -2(x_i - 1/2)e - e²
Thus,

If e < 0 then di > 0 so choose point S = (x_i - 1, y_i + 1).
d_i+1    = f(x_i - 1 - 1/2, y_i + 1 + 1) = ((x_i - 1/2) - 1)² + ((y_i + 1) + 1)² - r²
        = d_i - 2(x_i - 1) + 2(y_i + 1) + 1
        = d_i + 2(y_{i + 1} - x_{i + 1}) + 1
		  
If e >= 0 then di <= 0 so choose point T = (x_i, y_i + 1)
   d_i+1 = f(x_i - 1/2, y_i + 1 + 1)
       = d_i + 2y_i+1 + 1
		  
The initial value of di is
   d₀ = f(r - 1/2, 0 + 1) = (r - 1/2)² + 1² - r²
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (x_i - 1, y_i + 1) is chosen then
   d_i+1 = d_i + -2x_i+1 + 2y_i+1 + 1
	
When point T = (x_i, y_i + 1) is chosen then
   d_i+1 = d_i + 2y_i+1 + 1

Step 3 − K = 0から始まる各$ X_ {K} $位置で、次のテストを実行します−

If P_K < 0 then next point on circle (0,0) is (X_K+1,Y_K) and
   P_K+1 = P_K + 2X_K+1 + 1
Else
   P_K+1 = P_K + 2X_K+1 + 1 – 2Y_K+1
	
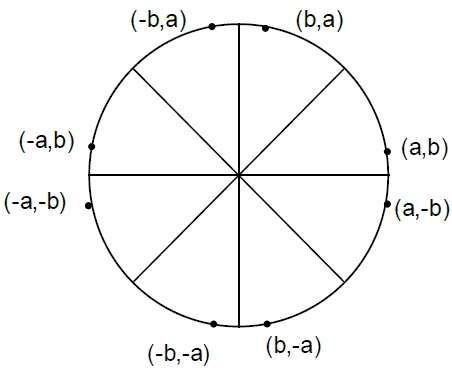
Where, 2X_K+1 = 2X_K+2 and 2Y_K+1 = 2Y_K-2.

Step 4 −他の7つの八分円の対称点を決定します。

Step 5 −各計算ピクセル位置（X、Y）を$（X_ {C、} Y_ {C}）$を中心とする円形パスに移動し、座標値をプロットします。

X = X + X_C,   Y = Y + Y_C

Step 6 − X> = Yになるまで、手順3〜5を繰り返します。