ポリゴン充填アルゴリズム
ポリゴンは、次の図に示すように、頂点の順序付きリストです。ポリゴンを特定の色で塗りつぶすには、ポリゴンの境界にあるピクセルとポリゴンの内側にあるピクセルを決定する必要があります。この章では、さまざまな手法を使用してポリゴンを塗りつぶす方法を説明します。

スキャンラインアルゴリズム
このアルゴリズムは、スキャンラインをポリゴンエッジと交差させることで機能し、交差のペア間でポリゴンを塗りつぶします。次の手順は、このアルゴリズムがどのように機能するかを示しています。
Step 1 −指定されたポリゴンからYminとYmaxを見つけます。
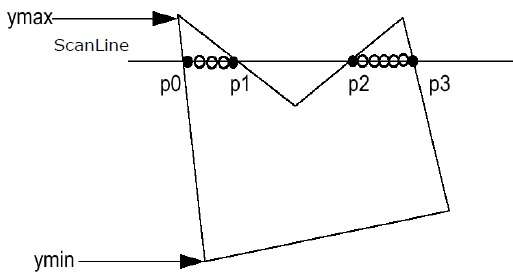
Step 2− ScanLineは、YminからYmaxまでのポリゴンの各エッジと交差します。ポリゴンの各交点に名前を付けます。上図のように、p0、p1、p2、p3という名前が付けられています。
Step 3 − X座標の昇順、つまり(p0、p1)、(p1、p2)、および(p2、p3)で交点を並べ替えます。
Step 4 −ポリゴン内にある座標のペアをすべて埋め、代替ペアを無視します。
フラッドフィルアルゴリズム
エリアとその境界を異なる色で塗りつぶしたいオブジェクトに出くわすことがあります。境界塗りつぶしアルゴリズムのように特定の境界色を検索する代わりに、指定された内部色でそのようなオブジェクトをペイントできます。
オブジェクトの境界に依存する代わりに、塗りつぶしの色に依存します。つまり、オブジェクトの内部の色を塗りつぶしの色に置き換えます。元の内部色のピクセルがなくなると、アルゴリズムが完了します。
繰り返しになりますが、このアルゴリズムは、ピクセルを埋める4接続または8接続の方法に依存しています。ただし、境界色を探す代わりに、内部の一部である隣接するすべてのピクセルを探します。
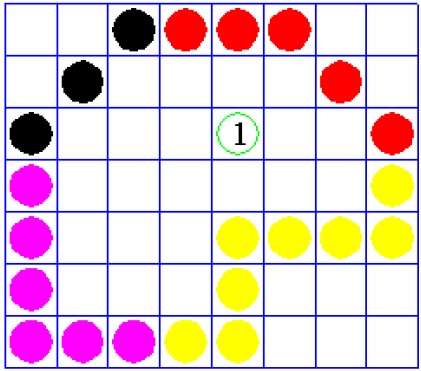
境界塗りつぶしアルゴリズム
境界塗りつぶしアルゴリズムはその名前として機能します。このアルゴリズムは、オブジェクト内のポイントを選択し、オブジェクトの境界に到達するまで塗りつぶしを開始します。このアルゴリズムが機能するには、境界の色と塗りつぶす色が異なっている必要があります。
このアルゴリズムでは、境界の色がオブジェクト全体で同じであると想定しています。境界塗りつぶしアルゴリズムは、4接続ピクセルまたは8接続ピクセルで実装できます。
4-接続されたポリゴン
この手法では、図に示すように4つの接続されたピクセルが使用されます。現在のピクセルの上、下、右、および左側にピクセルを配置しています。このプロセスは、異なる色の境界が見つかるまで続行されます。
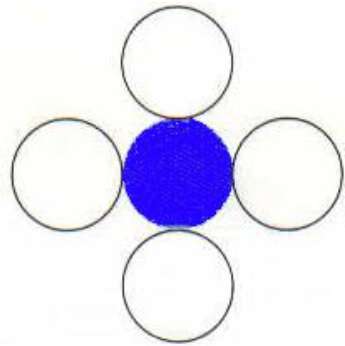
アルゴリズム
Step 1 −シードポイント(seedx、seedy)、fcolor、およびdcolの値を初期化します。
Step 2 −ポリゴンの境界値を定義します。
Step 3 −現在のシードポイントがデフォルトの色であるかどうかを確認し、境界ピクセルに達するまで手順4と5を繰り返します。
If getpixel(x, y) = dcol then repeat step 4 and 5Step 4 −シードポイントの塗りつぶし色でデフォルトの色を変更します。
setPixel(seedx, seedy, fcol)Step 5 −4つの近隣点を使用して手順を再帰的に実行します。
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)Step 6 −終了
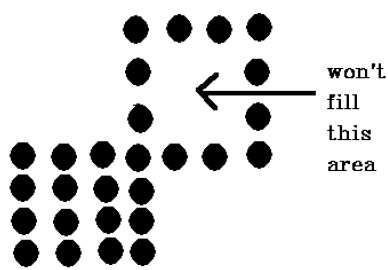
この手法には問題があります。以下に示すように、領域全体を埋めようとした場合を考えてみます。ここでは、画像は部分的にしか塗りつぶされていません。このような場合、4接続ピクセル技術は使用できません。
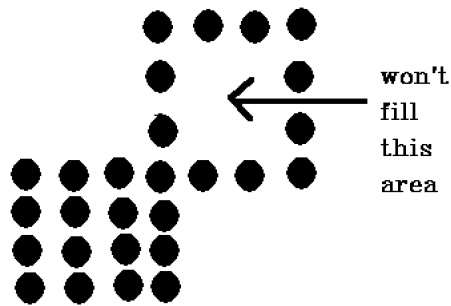
8-接続されたポリゴン
この手法では、図に示すように8つの接続されたピクセルが使用されます。4接続手法で行っていたように、現在のピクセルの上、下、右側、左側にピクセルを配置しています。
これに加えて、現在のピクセルの全領域がカバーされるように、ピクセルを対角線上に配置しています。このプロセスは、異なる色の境界が見つかるまで続きます。

アルゴリズム
Step 1 −シードポイント(seedx、seedy)、fcolor、およびdcolの値を初期化します。
Step 2 −ポリゴンの境界値を定義します。
Step 3 −現在のシードポイントがデフォルトの色であるかどうかを確認し、境界ピクセルに達するまで手順4と5を繰り返します。
If getpixel(x,y) = dcol then repeat step 4 and 5Step 4 −シードポイントの塗りつぶし色でデフォルトの色を変更します。
setPixel(seedx, seedy, fcol)Step 5 −4つの近隣点を使用して手順を再帰的に実行します
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)Step 6 −終了
次の図に示すように、4接続ピクセル手法では領域を埋めることができませんでした。これは8接続手法では発生しません。
内外テスト
この方法は、 counting number method。オブジェクトを塗りつぶすときに、特定のポイントがオブジェクトの内側にあるか外側にあるかを識別する必要があることがよくあります。特定のポイントがオブジェクトの内側にあるか外側にあるかを識別するには、2つの方法があります。
- 奇数-偶数ルール
- 非ゼロの回転数規則
奇数-偶数ルール
この手法では、任意の点(x、y)から無限大までの線に沿って交差するエッジをカウントします。相互作用の数が奇数の場合、点(x、y)は内部点です。相互作用の数が偶数の場合、点(x、y)は外部点です。次の例は、この概念を示しています。
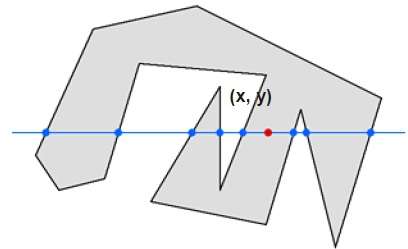
上の図から、点(x、y)から、左側の相互作用点の数は5、右側の相互作用点の数は3であることがわかります。両端から、相互作用点の数は奇数なので、ポイントはオブジェクト内で考慮されます。
ゼロ以外の回転数ルール
この方法は、特定のポイントが内部であるかどうかをテストするために、単純なポリゴンでも使用されます。ピンと輪ゴムで簡単に理解できます。ポリゴンの端の1つにピンを固定し、その中に輪ゴムを結び、ポリゴンの端に沿って輪ゴムを伸ばします。
ポリゴンのすべてのエッジが輪ゴムで覆われている場合は、テストするポイントで固定されているピンを確認します。ポイントで少なくとも1つの風が見つかった場合は、それをポリゴン内と見なします。それ以外の場合、ポイントはポリゴン内にないと言えます。
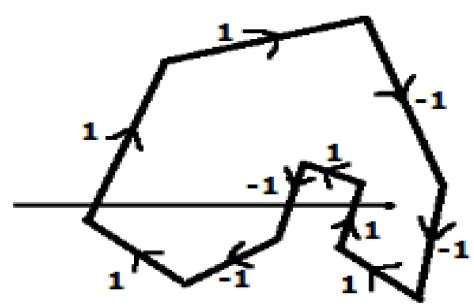
別の代替方法では、ポリゴンのすべてのエッジに方向を指定します。テストするポイントからX方向の左端に向かってスキャンラインを描画します。
上方向に向かうすべてのエッジに値1を指定し、方向の値として他のすべての-1を指定します。
スキャンラインが通過するエッジ方向の値を確認し、それらを合計します。
この方向の値の合計がゼロ以外の場合、テストされるこのポイントは interior point, それ以外の場合は exterior point。
上の図では、スキャンラインが通過する方向の値を合計すると、合計は1 – 1 + 1 = 1になります。これはゼロ以外です。したがって、ポイントは内部ポイントと呼ばれます。