コンピュータグラフィックス曲線
コンピュータグラフィックスでは、さまざまな種類のオブジェクトを画面に描画する必要があることがよくあります。オブジェクトは常にフラットではないため、オブジェクトを描画するには何度も曲線を描画する必要があります。
曲線の種類
曲線は、無限に大きな点のセットです。各ポイントには、エンドポイントを除いて2つのネイバーがあります。曲線は大きく3つのカテゴリに分類できます-explicit, implicit, そして parametric curves。
陰曲線
暗黙の曲線表現は、曲線上の点が入っているかどうかをテストできる手順を使用して、曲線上の点のセットを定義します。通常、陰曲線は次の形式の陰関数によって定義されます。
f(x、y)= 0
複数値の曲線(x値に対して複数のy値)を表すことができます。一般的な例は円であり、その暗黙の表現は
x2 + y2 - R2 = 0
明示的な曲線
数学関数y = f(x)を曲線としてプロットできます。このような関数は、曲線の明示的な表現です。明示的な表現は、垂直線を表すことができず、単一値でもあるため、一般的ではありません。xの値ごとに、通常、yの単一の値のみが関数によって計算されます。
パラメトリック曲線
パラメトリック形式の曲線は、パラメトリック曲線と呼ばれます。明示的および暗黙的な曲線表現は、関数がわかっている場合にのみ使用できます。実際には、パラメトリック曲線が使用されます。2次元のパラメトリック曲線は次の形式になります-
P(t)= f(t)、g(t)またはP(t)= x(t)、y(t)
関数fとgは、曲線上の任意の点の(x、y)座標になり、パラメーターtが特定の間隔[a、b]、通常は[0、1]にわたって変化したときに点が取得されます。
ベジェ曲線
ベジェ曲線はフランスのエンジニアによって発見されました Pierre Bézier。これらの曲線は、他のポイントの制御下で生成できます。制御点を使用した近似接線を使用して曲線を生成します。ベジェ曲線は数学的に次のように表すことができます-
$$ \ sum_ {k = 0} ^ {n} P_ {i} {B_ {i} ^ {n}}(t)$$
ここで、$ p_ {i} $は点の集合であり、$ {B_ {i} ^ {n}}(t)$は-で与えられるバーンスタイン多項式を表します。
$$ {B_ {i} ^ {n}}(t)= \ binom {n} {i}(1-t)^ {ni} t ^ {i} $$
どこ n は多項式の次数であり、 i はインデックスであり、 t は変数です。
最も単純なベジエ曲線は、点$ P_ {0} $から$ P_ {1} $までの直線です。二次ベジェ曲線は、3つの制御点によって決定されます。立方ベジェ曲線は、4つの制御点によって決定されます。
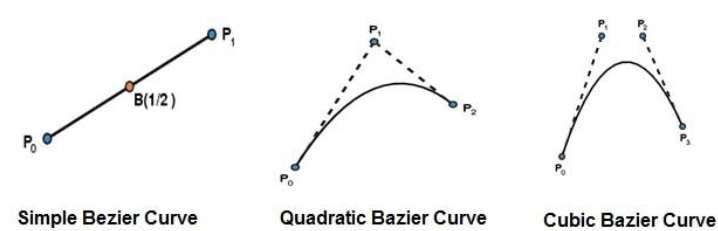
ベジェ曲線の特性
ベジェ曲線には次の特性があります-
これらは通常、コントロールポイントを結合するセグメントで構成されるコントロールポリゴンの形状に従います。
それらは常に最初と最後のコントロールポイントを通過します。
それらは、それらを定義する制御点の凸包に含まれています。
曲線セグメントを定義する多項式の次数は、定義するポリゴンポイントの数より1つ少なくなります。したがって、4つの制御点の場合、多項式の次数は3、つまり3次多項式です。
ベジェ曲線は通常、定義するポリゴンの形状に従います。
終点での接線ベクトルの方向は、最初と最後のセグメントによって決定されるベクトルの方向と同じです。
ベジェ曲線の凸包特性により、多項式が制御点にスムーズに従うことが保証されます。
制御ポリゴンと交差する回数よりも多くの回数、ベジェ曲線と交差する直線はありません。
それらはアフィン変換の下では不変です。
ベジェ曲線は、制御点を移動すると曲線全体の形状が変化するグローバル制御を示します。
与えられたベジェ曲線は、点t = t0で、パラメータ値t = t0に対応する点で結合する2つのベジェセグメントに分割できます。
B-スプライン曲線
バーンスタイン基底関数によって生成されるベジェ曲線の柔軟性は限られています。
まず、指定されたポリゴン頂点の数によって、曲線を定義する結果の多項式の順序が固定されます。
2番目の制限特性は、曲線全体のすべてのパラメーター値でブレンド関数の値がゼロ以外になることです。
Bスプライン基底には、特殊なケースとしてバーンスタイン基底が含まれています。Bスプラインベースは非グローバルです。
Bスプライン曲線は、制御点PiとBスプライン基底関数$ N_ {i、} $ k(t)の線形結合として定義されます。
$ C(t)= \ sum_ {i = 0} ^ {n} P_ {i} N_ {i、k}(t)、$ $ n \ geq k-1、$ $ t \:\ epsilon \:[ tk-1、tn + 1] $
どこ、
{$ p_ {i} $:i = 0、1、2….n}はコントロールポイントです
kは、Bスプライン曲線の多項式セグメントの次数です。次数kは、曲線が次数k-1の区分的多項式セグメントで構成されていることを意味します。
$ N_ {i、k}(t)$は、「正規化されたBスプラインブレンディング関数」です。それらは、次数kと、通常「ノットシーケンス」と呼ばれる実数の減少しないシーケンスによって記述されます。
$$ {t_ {i}:i = 0、... n + K} $$
N i、k関数は次のように記述されます-
$$ N_ {i、1}(t)= \ left \ {\ begin {matrix} 1、&if \:u \:\ epsilon \:[t_ {i、} t_ {i + 1})\\ 0 、&それ以外の場合は\ end {matrix} \ right。$$
k> 1の場合、
$$ N_ {i、k}(t)= \ frac {t-t_ {i}} {t_ {i + k-1}} N_ {i、k-1}(t)+ \ frac {t_ {i + k} -t} {t_ {i + k} -t_ {i + 1}} N_ {i + 1、k-1}(t)$$
そして
$$ t \:\ epsilon \:[t_ {k-1}、t_ {n + 1})$$
Bスプライン曲線の特性
Bスプライン曲線には次の特性があります-
任意のパラメーター値のBスプライン基底関数の合計は1です。
各基底関数は、すべてのパラメーター値に対して正またはゼロです。
k = 1を除いて、各基底関数には正確に1つの最大値があります。
曲線の最大次数は、ポリゴンを定義する頂点の数と同じです。
Bスプライン多項式の次数は、ポリゴンを定義する頂点の数に依存しません。
Bスプラインを使用すると、各頂点が、関連する基底関数がゼロ以外のパラメータ値の範囲でのみ曲線の形状に影響を与えるため、曲線サーフェスをローカルで制御できます。
曲線は、変動を減少させる特性を示しています。
曲線は通常、ポリゴンを定義する形状に従います。
ポリゴンを定義する頂点にアフィン変換を適用することにより、任意のアフィン変換を曲線に適用できます。
定義するポリゴンの凸包内の曲線。