ブール代数

ブール代数は、デジタル（論理）回路を分析および簡略化するために使用されます。0と1の2進数のみを使用します。Binary Algebra または logical Algebra。ブール代数はによって発明されましたGeorge Boole 1854年。

ブール代数のルール

以下は、ブール代数で使用される重要なルールです。

• 使用される変数は2つの値のみを持つことができます。HIGHの場合はバイナリ1、LOWの場合はバイナリ0。

• 変数の補集合は、オーバーバー（-）で表されます。したがって、変数Bの補集合はとして表され

  
  ます。したがって、B = 0の場合は
  
  = 1、B = 1の場合は
  
  = 0です。

• 変数のORは、変数間のプラス（+）記号で表されます。たとえば、A、B、CのORリングは、A + B + Cとして表されます。

• 2つ以上の変数の論理ANDは、ABCのようにそれらの間にドットを書き込むことによって表されます。ABCのようにドットが省略される場合があります。

ブール法

ブール法には6つのタイプがあります。

可換法則

次の式を満たす二項演算は、可換演算と呼ばれます。

可換法則によれば、変数の順序を変更しても、論理回路の出力には何の影響もありません。

結合法則

この法則は、論理演算が実行される順序は、その効果が同じであるため、無関係であると述べています。

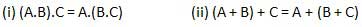
分配法則

分配法則は次の条件を述べています。

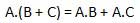
AND法

これらの法則はAND演算を使用します。したがって、それらは次のように呼ばれますAND 法律。

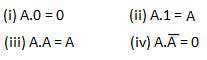
または法律

これらの法則はOR演算を使用します。したがって、それらは次のように呼ばれますOR 法律。

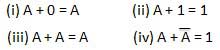
反転法

この法則はNOT演算を使用します。反転法則では、変数を2回反転すると、元の変数自体が生成されるとされています。

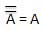
重要なブール定理

以下は、いくつかの重要なブール定理です。

ブール関数/定理	説明
ブール関数	ブール関数と式、KマップとNANDゲートの実現
ド・モルガンの定理	ド・モルガンの定理1と定理2