적응 공명 이론
이 네트워크는 1987 년 Stephen Grossberg와 Gail Carpenter가 개발했습니다. 경쟁을 기반으로하고 비지도 학습 모델을 사용합니다. 이름에서 알 수 있듯이 ART (Adaptive Resonance Theory) 네트워크는 이전 패턴 (공명)을 잃지 않고 항상 새로운 학습 (적응)에 개방되어 있습니다. 기본적으로 ART 네트워크는 입력 벡터를 받아들이고 저장된 패턴 중 가장 닮은 패턴에 따라 카테고리 중 하나로 분류하는 벡터 분류기입니다.
운영 원칙
ART 분류의 주요 작업은 다음 단계로 나눌 수 있습니다.
Recognition phase− 입력 벡터는 출력 레이어의 모든 노드에 제시된 분류와 비교됩니다. 뉴런의 출력은 적용된 분류와 가장 일치하면 "1"이되고 그렇지 않으면 "0"이됩니다.
Comparison phase−이 단계에서는 입력 벡터와 비교 계층 벡터를 비교합니다. 재설정 조건은 유사도가 경계 매개 변수보다 적다는 것입니다.
Search phase−이 단계에서 네트워크는 위의 단계에서 수행 된 일치뿐만 아니라 재설정을 검색합니다. 따라서 재설정이없고 경기가 꽤 좋은 경우 분류가 종료됩니다. 그렇지 않으면 프로세스가 반복되고 다른 저장된 패턴이 올바른 일치 항목을 찾기 위해 전송되어야합니다.
ART1
이진 벡터를 클러스터링하도록 설계된 ART 유형입니다. 우리는 그것의 아키텍처로 이것을 이해할 수 있습니다.
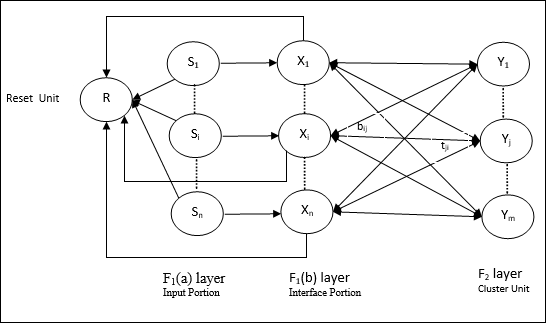
ART1의 아키텍처
그것은 다음 두 단위로 구성됩니다-
Computational Unit − 다음으로 구성되어 있습니다 −
Input unit (F1 layer) − 추가로 다음 두 부분이 있습니다 −
F1(a) layer (Input portion)− ART1에서는 입력 벡터 만있는 것이 아니라이 부분에서 처리가 없습니다. F 1 (b) 레이어 (인터페이스 부분)에 연결됩니다.
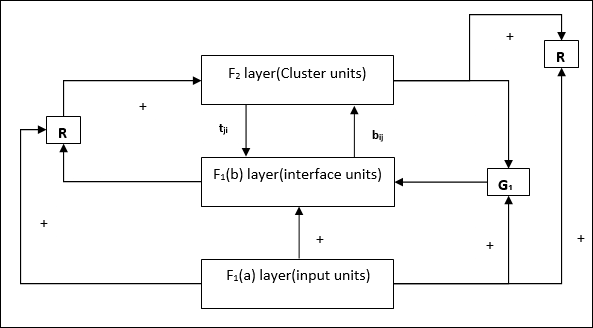
F1(b) layer (Interface portion)−이 부분은 입력 부분의 신호를 F 2 레이어 의 신호와 결합합니다 . F 1 (b) 레이어는 상향식 가중치를 통해 F 2 레이어에 연결됩니다.bijF 2 계층은 하향식 가중치를 통해 F 1 (b) 계층에 연결됩니다.tji.
Cluster Unit (F2 layer)− 이것은 경쟁 계층입니다. 입력 패턴을 학습하기 위해 순 입력이 가장 큰 단위를 선택합니다. 다른 모든 클러스터 장치의 활성화는 0으로 설정됩니다.
Reset Mechanism−이 메커니즘의 작업은 하향식 가중치와 입력 벡터 간의 유사성을 기반으로합니다. 이제이 유사성의 정도가 경계 매개 변수보다 작 으면 클러스터가 패턴을 학습 할 수 없으며 나머지가 발생합니다.
Supplement Unit − 실제로 재설정 메커니즘의 문제는 레이어가 F2특정 조건 하에서 금지되어야하며 학습이 발생할 때도 사용할 수 있어야합니다. 그래서 두 개의 보조 단위 즉,G1 과 G2 리셋 유닛과 함께 추가됩니다. R. 그들 불리는gain control units. 이 장치는 네트워크에있는 다른 장치로 신호를 수신하고 보냅니다.‘+’ 흥분성 신호를 나타내는 반면 ‘−’ 억제 신호를 나타냅니다.
사용 된 매개 변수
다음 매개 변수가 사용됩니다-
n − 입력 벡터의 성분 수
m − 형성 할 수있는 최대 클러스터 수
bij− F 1 (b)에서 F 2 레이어까지의 가중치, 즉 상향식 가중치
tji− F 2 에서 F 1 (b) 레이어까지의 가중치, 즉 하향식 가중치
ρ − 경계 매개 변수
||x|| − 벡터 x의 놈
연산
Step 1 − 다음과 같이 학습률, 경계 매개 변수 및 가중치를 초기화합니다.
$$ \ alpha \ :> \ : 1 \ : \ : and \ : \ : 0 \ : <\ rho \ : \ leq \ : 1 $$
$$ 0 \ : <\ : b_ {ij} (0) \ : <\ : \ frac {\ alpha} {\ alpha \ :-\ : 1 \ : + \ : n} \ : \ : and \ : \ : t_ {ij} (0) \ : = \ : 1 $$
Step 2 − 중지 조건이 참이 아닌 경우 3-9 단계를 계속합니다.
Step 3 − 모든 교육 입력에 대해 4-6 단계를 계속합니다.
Step 4− 다음과 같이 모든 F 1 (a) 및 F 1 장치의 활성화를 설정 합니다.
F2 = 0 and F1(a) = input vectors
Step 5− F 1 (a)에서 F 1 (b) 레이어 까지의 입력 신호 는 다음과 같이 전송되어야합니다.
$$ s_ {i} \ : = \ : x_ {i} $$
Step 6− 모든 금지 된 F 2 노드에 대해
$ y_ {j} \ : = \ : \ sum_i b_ {ij} x_ {i} $ 조건은 yj ≠ -1
Step 7 − 재설정이 참이면 8-10 단계를 수행합니다.
Step 8 − 찾기 J ...에 대한 yJ ≥ yj 모든 노드 j
Step 9− F 1 (b) 에 대한 활성화를 다시 다음과 같이 계산 합니다.
$$ x_ {i} \ : = \ : sitJi $$
Step 10 − 이제 벡터의 노름을 계산 한 후 x 및 벡터 s, 다음과 같이 리셋 조건을 확인해야합니다.
만약 ||x||/ ||s|| <경계 매개 변수 ρ, theninhibit node J 7 단계로 이동
Else If ||x||/ ||s|| ≥ 경계 매개 변수 ρ을 누른 다음 계속 진행하십시오.
Step 11 − 노드에 대한 가중치 업데이트 J 다음과 같이 할 수 있습니다-
$$ b_ {ij} (신규) \ : = \ : \ frac {\ alpha x_ {i}} {\ alpha \ :-\ : 1 \ : + \ : || x ||} $$
$$ t_ {ij} (신규) \ : = \ : x_ {i} $$
Step 12 − 알고리즘의 정지 조건을 확인해야하며 다음과 같을 수 있습니다 −
- 체중 변화가 없습니다.
- 장치에 대해서는 재설정이 수행되지 않습니다.
- 최대 Epoch 수에 도달했습니다.