Hopfield 네트워크를 사용한 최적화
최적화는 설계, 상황, 자원 및 시스템과 같은 것을 가능한 한 효과적으로 만드는 조치입니다. 비용 함수와 에너지 함수의 유사점을 사용하여 고도로 상호 연결된 뉴런을 사용하여 최적화 문제를 해결할 수 있습니다. 이러한 종류의 신경망은 하나 이상의 완전히 연결된 반복 뉴런을 포함하는 단일 계층으로 구성된 Hopfield 네트워크입니다. 최적화에 사용할 수 있습니다.
최적화를 위해 Hopfield 네트워크를 사용하는 동안 기억해야 할 사항-
에너지 기능은 네트워크의 최소값이어야합니다.
저장된 패턴 중 하나를 선택하는 대신 만족스러운 솔루션을 찾을 수 있습니다.
Hopfield 네트워크에서 찾은 솔루션의 품질은 네트워크의 초기 상태에 따라 크게 달라집니다.
여행하는 세일즈맨 문제
세일즈맨이 이동 한 최단 경로를 찾는 것은 연산 문제 중 하나이며 Hopfield 신경망을 사용하여 최적화 할 수 있습니다.
TSP의 기본 개념
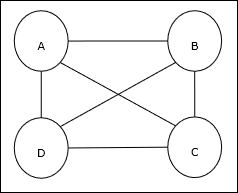
출장 세일즈맨 문제 (TSP)는 세일즈맨이 출장해야하는 고전적인 최적화 문제입니다. n비용과 이동 거리를 최소화하면서 서로 연결된 도시. 예를 들어, 세일즈맨은 4 개 도시 A, B, C, D를 여행해야하며 목표는 가장 짧은 순환 여행 인 ABC–D를 찾아 비용을 최소화하는 것입니다. 여기에는 여행 비용도 포함됩니다. 마지막 도시 D에서 첫 번째 도시 A까지.
행렬 표현
실제로 n-city TSP의 각 투어는 다음과 같이 표현할 수 있습니다. n × n 매트릭스 ith 행은 ith도시의 위치. 이 매트릭스,M, 4 개 도시의 경우 A, B, C, D는 다음과 같이 표현할 수 있습니다.
$$ M = \ begin {bmatrix} A : & 1 & 0 & 0 & 0 \\ B : & 0 & 1 & 0 & 0 \\ C : & 0 & 0 & 1 & 0 \\ D : & 0 & 0 & 0 & 1 \ end {bmatrix} $$
Hopfield Network의 솔루션
Hopfield 네트워크에서이 TSP의 솔루션을 고려하는 동안 네트워크의 모든 노드는 매트릭스의 한 요소에 해당합니다.
에너지 함수 계산
최적화 된 솔루션이 되려면 에너지 함수가 최소 여야합니다. 다음과 같은 제약을 기반으로 에너지 함수를 다음과 같이 계산할 수 있습니다.
제약 -I
에너지 함수를 계산하는 데 기초한 첫 번째 제약은 행렬의 각 행에서 한 요소가 1과 같아야한다는 것입니다. M 각 행의 다른 요소는 다음과 같아야합니다. 0각 도시는 TSP 투어에서 한 위치에서만 발생할 수 있기 때문입니다. 이 제약은 수학적으로 다음과 같이 작성할 수 있습니다.
$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j} \ : = \ : 1 \ : for \ : x \ : \ in \ : \ lbrace1, ..., n \ rbrace $ $
이제 최소화 할 에너지 함수는 위의 제약 조건에 따라 다음에 비례하는 항을 포함합니다.
$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \ :-\ : \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j } \ end {배열} \ right) ^ 2 $$
제약 II
아시다시피, TSP에서 하나의 도시는 여행의 어느 위치에서나 발생할 수 있으므로 행렬의 각 열에서 M, 한 요소는 1과 같아야하고 다른 요소는 0과 같아야합니다.이 제약은 수학적으로 다음과 같이 작성할 수 있습니다.
$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j} \ : = \ : 1 \ : for \ : j \ : \ in \ : \ lbrace1, ..., n \ rbrace $ $
이제 최소화 할 에너지 함수는 위의 제약 조건에 따라 다음에 비례하는 항을 포함합니다.
$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \ :-\ : \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j } \ end {배열} \ right) ^ 2 $$
비용 함수 계산
(n × n) 표시 C TSP의 비용 매트릭스를 나타냅니다. n 어디에 n > 0. 다음은 비용 함수를 계산하는 동안 몇 가지 매개 변수입니다.
Cx, y − 비용 매트릭스의 요소는 도시에서 여행하는 비용을 나타냅니다. x ...에 y.
A와 B 요소의 인접성은 다음 관계식으로 표시 할 수 있습니다.
$$ M_ {x, i} \ : = \ : 1 \ : \ : 및 \ : \ : M_ {y, i \ pm 1} \ : = \ : 1 $$
아시다시피 Matrix에서 각 노드의 출력 값은 0 또는 1이 될 수 있으므로 모든 도시 A, B 쌍에 대해 에너지 함수에 다음 항을 추가 할 수 있습니다.
$$ \ displaystyle \ sum \ limits_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \ : + \ : M_ {y, i-1}) $$
위의 비용 함수 및 제약 값을 기반으로 최종 에너지 함수 E 다음과 같이 주어질 수 있습니다-
$$ E \ : = \ : \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {x} \ displaystyle \ sum \ limits_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \ : + \ : M_ {y, i-1}) \ : + $$
$$ \ : \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limits_ {x} \ left (\ begin {array} {c} 1 \ :-\ : \ displaystyle \ sum \ limits_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \ : + \ : \ gamma_ {2} \ displaystyle \ sum \ limits_ {i} \ left (\ begin {array} {c} 1 \ :-\ : \ displaystyle \ sum \ limits_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$
여기, γ1 과 γ2 두 개의 계량 상수입니다.