볼츠만 기계
이는 반복적 인 구조를 갖는 확률 적 학습 프로세스이며 ANN에서 사용되는 초기 최적화 기술의 기초입니다. Boltzmann Machine은 1985 년 Geoffrey Hinton과 Terry Sejnowski에 의해 발명되었습니다. Boltzmann Machine에 대한 Hinton의 말에서 더 명확하게 확인할 수 있습니다.
“이 네트워크의 놀라운 기능은 로컬에서 사용 가능한 정보 만 사용한다는 것입니다. 무게의 변화는 비록 변화가 글로벌 측정을 최적화하더라도 연결하는 두 단위의 행동에만 의존합니다.”-Ackley, Hinton 1985.
Boltzmann Machine에 대한 몇 가지 중요한 사항-
그들은 반복적 인 구조를 사용합니다.
그것들은 확률 론적 뉴런으로 구성되며, 1 또는 0의 두 가지 가능한 상태 중 하나를 가지고 있습니다.
이 뉴런 중 일부는 적응 형 (자유 상태)이고 일부는 고정 (고정 상태)입니다.
이산 Hopfield 네트워크에 시뮬레이션 어닐링을 적용하면 Boltzmann Machine이됩니다.
Boltzmann Machine의 목표
Boltzmann Machine의 주요 목적은 문제 해결을 최적화하는 것입니다. 특정 문제와 관련된 무게와 수량을 최적화하는 것이 Boltzmann Machine의 작업입니다.
건축물
다음 다이어그램은 Boltzmann 기계의 아키텍처를 보여줍니다. 다이어그램을 보면 단위의 2 차원 배열임을 알 수 있습니다. 여기서 장치 간의 상호 연결에 대한 가중치는 다음과 같습니다.–p 어디 p > 0. 자기 연결의 가중치는 다음과 같습니다.b 어디 b > 0.
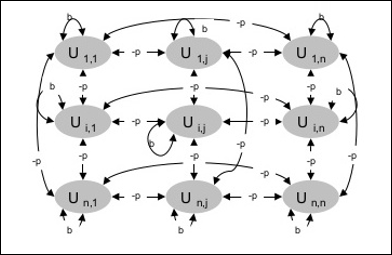
훈련 알고리즘
Boltzmann 기계에는 고정 된 가중치가 있으므로 네트워크에서 가중치를 업데이트 할 필요가 없으므로 훈련 알고리즘이 없습니다. 그러나 네트워크를 테스트하려면 가중치를 설정하고 합의 함수 (CF)를 찾아야합니다.
Boltzmann 기계에는 일련의 단위가 있습니다. Ui 과 Uj 양방향 연결이 있습니다.
우리는 고정 된 무게를 고려하고 있습니다 wij.
wij ≠ 0 만약 Ui 과 Uj 연결되어있다.
가중 상호 연결에도 대칭이 있습니다. wij = wji.
wii 즉, 장치간에 자체 연결이 있습니다.
모든 단위 Ui, 상태 ui 1 또는 0입니다.
Boltzmann Machine의 주요 목적은 다음 관계로 주어질 수있는 합의 함수 (CF)를 극대화하는 것입니다.
$$ CF \ : = \ : \ displaystyle \ sum \ limits_ {i} \ displaystyle \ sum \ limits_ {j \ leqslant i} w_ {ij} u_ {i} u_ {j} $$
이제 상태가 1에서 0으로 또는 0에서 1로 변경되면 합의의 변화는 다음 관계식으로 주어질 수 있습니다.
$$ \ 델타 CF \ : = \ :( 1 \ :-\ : 2u_ {i}) (w_ {ij} \ : + \ : \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$
여기 ui 현재 상태 Ui.
계수의 변동 (1 - 2ui)는 다음 관계식으로 주어집니다-
$$ (1 \ :-\ : 2u_ {i}) \ : = \ : \ begin {cases} +1, & U_ {i} \ : is \ : currently \ : off \\-1, & U_ {i } \ : is \ : 현재 \ : on \ end {cases} $$
일반적으로 단위 Ui상태를 변경하지 않지만 변경하면 정보는 해당 장치의 로컬에 상주합니다. 이러한 변화로 인해 네트워크의 합의도 증가 할 것입니다.
네트워크가 장치 상태의 변화를 수용 할 확률은 다음 관계식으로 제공됩니다.
$$ AF (i, T) \ : = \ : \ frac {1} {1 \ : + \ : exp [-\ frac {\ Delta CF (i)} {T}]} $$
여기, T제어 매개 변수입니다. CF가 최대 값에 도달하면 감소합니다.
테스트 알고리즘
Step 1 − 교육을 시작하려면 다음을 초기화하세요 −
- 문제의 제약을 나타내는 가중치
- 제어 매개 변수 T
Step 2 − 중지 조건이 참이 아닌 경우 3-8 단계를 계속합니다.
Step 3 − 4-7 단계를 수행합니다.
Step 4 − 상태 중 하나가 가중치를 변경했다고 가정하고 정수를 선택합니다. I, J 사이의 임의 값으로 1 과 n.
Step 5 − 다음과 같이 합의의 변화를 계산합니다 −
$$ \ 델타 CF \ : = \ :( 1 \ :-\ : 2u_ {i}) (w_ {ij} \ : + \ : \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$
Step 6 −이 네트워크가 상태 변화를 받아 들일 확률을 계산합니다.
$$ AF (i, T) \ : = \ : \ frac {1} {1 \ : + \ : exp [-\ frac {\ Delta CF (i)} {T}]} $$
Step 7 − 다음과 같이이 변경 사항을 수락하거나 거부합니다.
Case I − 만약 R < AF, 변경 사항을 수락합니다.
Case II − 만약 R ≥ AF, 변경을 거부합니다.
여기, R 0과 1 사이의 난수입니다.
Step 8 − 다음과 같이 제어 매개 변수 (온도)를 줄입니다.
T(new) = 0.95T(old)
Step 9 − 다음과 같은 정지 조건 테스트 −
- 온도가 지정된 값에 도달
- 지정된 반복 횟수에 대한 상태 변경이 없습니다.