Kohonen 자체 구성 기능 맵
임의의 차원 패턴이 있지만 1 차원 또는 2 차원에서 필요하다고 가정합니다. 그러면 기능 매핑 프로세스는 넓은 패턴 공간을 일반적인 기능 공간으로 변환하는 데 매우 유용합니다. 자, 왜 우리는 자기 조직화 기능 맵이 필요한가? 그 이유는 임의의 차원을 1-D 또는 2-D로 변환하는 기능과 함께 인접 토폴로지를 보존하는 기능도 가져야하기 때문입니다.
Kohonen SOM의 인접 토폴로지
다양한 토폴로지가있을 수 있지만 다음 두 토폴로지가 가장 많이 사용됩니다.
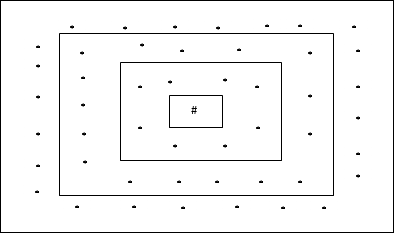
직사각형 그리드 토폴로지
이 토폴로지에는 distance-2 그리드에 24 개 노드, distance-1 그리드에 16 개 노드, distance-0 그리드에 8 개 노드가 있습니다. 즉, 각 직사각형 그리드 간의 차이는 8 개 노드입니다. 우승 한 단위는 #으로 표시됩니다.
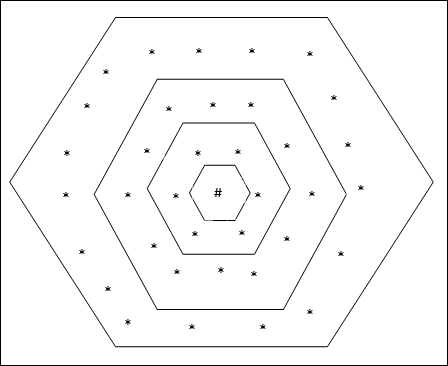
육각 그리드 토폴로지
이 토폴로지에는 distance-2 그리드에 18 개 노드, distance-1 그리드에 12 개 노드, distance-0 그리드에 6 개 노드가 있습니다. 즉, 각 직사각형 그리드 간의 차이는 6 개 노드입니다. 우승 한 단위는 #으로 표시됩니다.
건축물
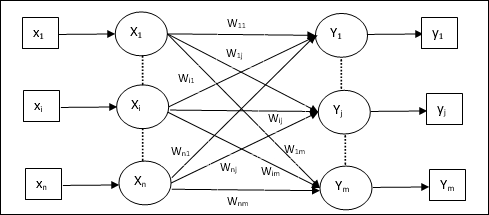
KSOM의 아키텍처는 경쟁 네트워크의 아키텍처와 유사합니다. 앞에서 논의한 이웃 계획의 도움으로 교육은 네트워크의 확장 된 영역에서 수행 될 수 있습니다.
훈련을위한 알고리즘
Step 1 − 가중치, 학습률 초기화 α 그리고 이웃 토폴로지 체계.
Step 2 − 중지 조건이 참이 아닌 경우 3-9 단계를 계속합니다.
Step 3 − 모든 입력 벡터에 대해 4-6 단계를 계속합니다. x.
Step 4 −에 대한 유클리드 거리의 제곱 계산 j = 1 to m
$$ D (j) \ : = \ : \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ m (x_ {i} \ :-\ : w_ {ij }) ^ 2 $$
Step 5 − 우승 유닛 획득 J 어디 D(j) 최소입니다.
Step 6 − 다음 관계식으로 우승 한 유닛의 새 가중치를 계산합니다. −
$$ w_ {ij} (신규) \ : = \ : w_ {ij} (이전) \ : + \ : \ alpha [x_ {i} \ :-\ : w_ {ij} (이전)] $$
Step 7 − 학습률 업데이트 α 다음 관계에 의해-
$$ \ alpha (t \ : + \ : 1) \ : = \ : 0.5 \ alpha t $$
Step 8 − 토폴로지 구조의 반경을 줄입니다.
Step 9 − 네트워크의 정지 상태를 확인하십시오.