인공 신경망-Hopfield Networks
Hopfield 신경망은 1982 년 John J. Hopfield 박사에 의해 발명되었습니다. 이것은 하나 이상의 완전히 연결된 반복 뉴런을 포함하는 단일 계층으로 구성됩니다. Hopfield 네트워크는 일반적으로 자동 연결 및 최적화 작업에 사용됩니다.
이산 홉 필드 네트워크
이산 라인 방식 또는 즉, 입력 및 출력 패턴이 이산 벡터라고 말할 수있는 Hopfield 네트워크는 본질적으로 이진 (0,1) 또는 양극 (+1, -1) 일 수 있습니다. 네트워크에는 자체 연결이없는 대칭 가중치가 있습니다.wij = wji 과 wii = 0.
건축물
다음은 이산 Hopfield 네트워크에 대해 염두에 두어야 할 몇 가지 중요한 사항입니다.
이 모델은 하나의 반전 출력과 하나의 비 반전 출력이있는 뉴런으로 구성됩니다.
각 뉴런의 출력은 다른 뉴런의 입력이어야하지만 self의 입력이 아니어야합니다.
무게 / 연결 강도는 다음과 같이 표시됩니다. wij.
연결은 자극적 일뿐만 아니라 억제적일 수 있습니다. 뉴런의 출력이 입력과 같으면 흥분하고 그렇지 않으면 억제합니다.
가중치는 대칭이어야합니다. 즉 wij = wji
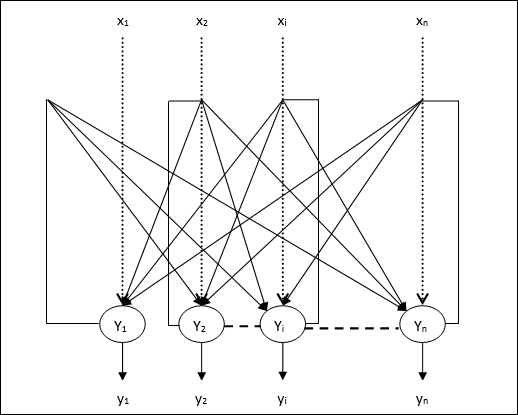
출력 Y1 가는 Y2, Yi 과 Yn 무게가있다 w12, w1i 과 w1n각기. 마찬가지로, 다른 호에는 가중치가 있습니다.
훈련 알고리즘
이산 Hopfield 네트워크를 훈련하는 동안 가중치가 업데이트됩니다. 우리가 알고 있듯이 이진 입력 벡터와 양극 입력 벡터를 가질 수 있습니다. 따라서 두 경우 모두 다음 관계식으로 가중치 업데이트를 수행 할 수 있습니다.
Case 1 − 이진 입력 패턴
바이너리 패턴 세트의 경우 s(p), p = 1 to P
여기, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
가중치 매트릭스는 다음과 같이 제공됩니다.
$$ w_ {ij} \ : = \ : \ sum_ {p = 1} ^ P [2s_ {i} (p)-\ : 1] [2s_ {j} (p)-\ : 1] \ : \ : \ : \ : \ : for \ : i \ : \ neq \ : j $$
Case 2 − 바이폴라 입력 패턴
바이너리 패턴 세트의 경우 s(p), p = 1 to P
여기, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
가중치 매트릭스는 다음과 같이 제공됩니다.
$$ w_ {ij} \ : = \ : \ sum_ {p = 1} ^ P [s_ {i} (p)] [s_ {j} (p)] \ : \ : \ : \ : \ : for \ : i \ : \ neq \ : j $$
테스트 알고리즘
Step 1 − Hebbian 원리를 사용하여 훈련 알고리즘에서 얻은 가중치를 초기화합니다.
Step 2 − 네트워크 활성화가 통합되지 않은 경우 3-9 단계를 수행합니다.
Step 3 − 각 입력 벡터에 대해 X, 4-8 단계를 수행합니다.
Step 4 − 네트워크의 초기 활성화를 외부 입력 벡터와 동일하게 만듭니다. X 다음과 같이-
$$ y_ {i} \ : = \ : x_ {i} \ : \ : \ : for \ : i \ : = \ : 1 \ : to \ : n $$
Step 5 − 각 유닛 Yi, 6-9 단계를 수행합니다.
Step 6 − 다음과 같이 네트워크의 순 입력을 계산합니다 −
$$ y_ {ini} \ : = \ : x_ {i} \ : + \ : \ displaystyle \ sum \ limits_ {j} y_ {j} w_ {ji} $$
Step 7 − 순 입력에 다음과 같이 활성화를 적용하여 출력을 계산합니다. −
$$ y_ {i} \ : = \ begin {cases} 1 & if \ : y_ {ini} \ :> \ : \ theta_ {i} \\ y_ {i} & if \ : y_ {ini} \ : = \ : \ theta_ {i} \\ 0 & if \ : y_ {ini} \ : <\ : \ theta_ {i} \ end {cases} $$
여기서 $ \ theta_ {i} $가 임계 값입니다.
Step 8 −이 출력 브로드 캐스트 yi 다른 모든 단위에.
Step 9 − 연결을 위해 네트워크를 테스트합니다.
에너지 기능 평가
에너지 기능은 결합 된 기능과 시스템 상태의 비 증가 기능으로 정의됩니다.
에너지 기능 Ef, 라고도 함 Lyapunov function 이산 Hopfield 네트워크의 안정성을 결정하며 다음과 같은 특징이 있습니다.
$$ E_ {f} \ : = \ :-\ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ n y_ {i} y_ {j} w_ {ij} \ :-\ : \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} y_ {i} \ : + \ : \ displaystyle \ sum \ limits_ {i = 1} ^ n \ theta_ {i} y_ {i} $$
Condition − 안정적인 네트워크에서는 노드의 상태가 변할 때마다 위의 에너지 기능이 감소합니다.
노드가 i 상태를 $ y_i ^ {(k)} $에서 $ y_i ^ {(k \ : + \ : 1)} $로 변경 한 다음 에너지 변화 $ \ Delta E_ {f} $는 다음 관계식으로 제공됩니다.
$$ \ 델타 E_ {f} \ : = \ : E_ {f} (y_i ^ {(k + 1)}) \ :-\ : E_ {f} (y_i ^ {(k)}) $$
$$ = \ :-\ left (\ begin {array} {c} \ displaystyle \ sum \ limits_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \ : + \ : x_ {i} \ :-\ : \ theta_ {i} \ end {array} \ right) (y_i ^ {(k + 1)} \ :-\ : y_i ^ {(k)}) $$
$$ = \ :-\ :( net_ {i}) \ Delta y_ {i} $$
여기 $ \ Delta y_ {i} \ : = \ : y_i ^ {(k \ : + \ : 1)} \ :-\ : y_i ^ {(k)} $
에너지의 변화는 한 번에 하나의 장치 만 활성화를 업데이트 할 수 있다는 사실에 달려 있습니다.
연속 홉 필드 네트워크
Discrete Hopfield 네트워크와 비교하여 연속 네트워크는 연속 변수로 시간이 있습니다. 또한 여행하는 세일즈맨 문제와 같은 자동 연결 및 최적화 문제에도 사용됩니다.
Model − 시그 모이 드 활성화 기능을 통해 입력 전압을 출력 전압에 매핑 할 수있는 증폭기와 같은 전기 부품을 추가하여 모델 또는 아키텍처를 구축 할 수 있습니다.
에너지 기능 평가
$$ E_f = \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} -\ displaystyle \ sum \ limits_ {i = 1} ^ n x_i y_i + \ frac {1} {\ lambda} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {-1} (y) dy $$
여기 λ 이득 매개 변수이고 gri 입력 전도도.