학습 및 적응

앞서 언급했듯이 ANN은 생물학적 신경계, 즉 인간의 뇌가 작동하는 방식에서 완전히 영감을 받았습니다. 인간 두뇌의 가장 인상적인 특징은 학습하는 것이므로 ANN은 동일한 기능을 획득합니다.

ANN에서 학습이란 무엇입니까?

기본적으로 학습이란 환경의 변화가있을 때 그 자체로 변화를 수행하고 적응하는 것을 의미합니다. ANN은 복잡한 시스템이거나보다 정확하게는 그것이 통과하는 정보를 기반으로 내부 구조를 변경할 수있는 복잡한 적응 시스템이라고 말할 수 있습니다.

왜 중요 함?

복잡한 적응 시스템이기 때문에 ANN에서 학습한다는 것은 처리 장치가 환경의 변화로 인해 입력 / 출력 동작을 변경할 수 있음을 의미합니다. ANN에서 학습의 중요성은 특정 네트워크가 구성 될 때 입력 / 출력 벡터뿐만 아니라 고정 된 활성화 함수로 인해 증가합니다. 이제 입력 / 출력 동작을 변경하려면 가중치를 조정해야합니다.

분류

동일한 클래스의 샘플 간의 공통 특징을 찾아서 샘플의 데이터를 다른 클래스로 구분하는 학습 과정으로 정의 할 수있다. 예를 들어 ANN 교육을 수행하기 위해 고유 한 기능이있는 일부 교육 샘플이 있고 테스트를 수행하기 위해 다른 고유 한 기능이있는 일부 테스트 샘플이 있습니다. 분류는지도 학습의 한 예입니다.

신경망 학습 규칙

ANN 학습 중에 입력 / 출력 동작을 변경하려면 가중치를 조정해야합니다. 따라서 가중치를 수정할 수있는 방법이 필요합니다. 이러한 방법을 학습 규칙이라고하며 단순히 알고리즘 또는 방정식입니다. 다음은 신경망에 대한 몇 가지 학습 규칙입니다.

Hebbian 학습 규칙

가장 오래되고 단순한 규칙 중 하나 인이 규칙은 Donald Hebb 가 1949 년 그의 저서 The Organization of Behavior 에서 소개했습니다. 일종의 피드 포워드, 비지도 학습입니다.

Basic Concept −이 규칙은 Hebb이 작성한 제안에 기반합니다.

“세포 A의 축색 돌기가 세포 B를 자극 할만큼 충분히 가까워서 반복적으로 또는 지속적으로 그것을 발사하는 데 참여할 때, 일부 성장 과정 또는 대사 변화가 하나 또는 두 세포에서 발생하여 A의 효율성이 B를 발사하는 세포 중 하나처럼 , 증가합니다. "

위의 가정에서 우리는 뉴런이 동시에 발화하면 두 뉴런 사이의 연결이 강화되고 다른 시간에 발화하면 약해질 수 있다는 결론을 내릴 수 있습니다.

Mathematical Formulation − Hebbian 학습 규칙에 따라 매 시간 단계에서 연결 가중치를 높이는 공식은 다음과 같습니다.

$$ \ 델타 w_ {ji} (t) \ : = \ : \ alpha x_ {i} (t) .y_ {j} (t) $$

여기에서 $ \ Delta w_ {ji} (t) $ ⁡ = 시간 단계에서 연결 가중치가 증가하는 증가분 t

$ \ alpha $ = 긍정적이고 일정한 학습률

$ x_ {i} (t) $ = 시간 단계에서 시냅스 전 뉴런의 입력 값 t

$ y_ {i} (t) $ = 동일한 시간 단계에서 시냅스 전 뉴런의 출력 t

퍼셉트론 학습 규칙

이 규칙은 Rosenblatt에서 도입 한 선형 활성화 함수를 사용하는 단일 레이어 피드 포워드 네트워크의지도 학습 알고리즘을 수정하는 오류입니다.

Basic Concept− 본질적으로 감독되기 때문에 오류를 계산하기 위해 원하는 / 목표 출력과 실제 출력을 비교합니다. 차이가 발견되면 연결 가중치를 변경해야합니다.

Mathematical Formulation − 수학적 공식을 설명하기 위해 원하는 / 타겟 출력 벡터 t (n)와 함께 유한 입력 벡터 x (n)의 'n'개가 있다고 가정합니다. 여기서 n = 1 ~ N입니다.

이제 출력 'y'는 앞서 설명한 순 입력을 기반으로 계산할 수 있으며 해당 순 입력에 적용되는 활성화 함수는 다음과 같이 표현할 수 있습니다.

$$ y \ : = \ : f (y_ {in}) \ : = \ : \ begin {cases} 1, & y_ {in} \ :> \ : \ theta \\ 0, & y_ {in} \ : \ leqslant \ : \ theta \ end {cases} $$

어디 θ 임계 값입니다.

가중치 업데이트는 다음 두 가지 경우에 수행 할 수 있습니다.

Case I − 언제 t ≠ y, 다음

$$ w (신규) \ : = \ : w (이전) \ : + \; tx $$

Case II − 언제 t = y, 다음

체중 변화 없음

델타 학습 규칙 (Widrow-Hoff 규칙)

이는 모든 훈련 패턴에 대한 오류를 최소화하기 위해 LMS (Least Mean Square) 방법이라고도하는 Bernard Widrow와 Marcian Hoff에 의해 도입되었습니다. 지속적인 활성화 기능을 가진 일종의지도 학습 알고리즘입니다.

Basic Concept−이 규칙의 기본은 계속되는 경사 하강 법입니다. 델타 규칙은 출력 단위 및 목표 값에 대한 순 입력을 최소화하기 위해 시냅스 가중치를 업데이트합니다.

Mathematical Formulation − 시냅스 가중치를 업데이트하기 위해 델타 규칙은

$$ \ 델타 w_ {i} \ : = \ : \ alpha \ :. x_ {i} .e_ {j} $$

여기서 $ \ Delta w_ {i} $ = i ^번째 ⁡ 패턴에 대한 무게 변화 ;

$ \ alpha $ = 긍정적이고 지속적인 학습률;

$ x_ {i} $ = 시냅스 전 뉴런의 입력 값;

$ e_ {j} $ = $ (t \ :-\ : y_ {in}) $, 원하는 / 목표 출력과 실제 출력의 차이 ⁡ $ y_ {in} $

위의 델타 규칙은 단일 출력 장치에만 적용됩니다.

가중치 업데이트는 다음 두 가지 경우에 수행 할 수 있습니다.

Case-I − 언제 t ≠ y, 다음

$$ w (신규) \ : = \ : w (이전) \ : + \ : \ Delta w $$

Case-II − 언제 t = y, 다음

체중 변화 없음

경쟁 학습 규칙 (승자 독식)

출력 노드가 입력 패턴을 나타 내기 위해 서로 경쟁을 시도하는 비지도 학습과 관련이 있습니다. 이 학습 규칙을 이해하려면 다음과 같은 경쟁 네트워크를 이해해야합니다.

Basic Concept of Competitive Network−이 네트워크는 출력 간 피드백 연결이있는 단일 레이어 피드 포워드 네트워크와 같습니다. 출력 간의 연결은 점선으로 표시되는 금지 유형이므로 경쟁자가 스스로를 지원하지 않음을 의미합니다.

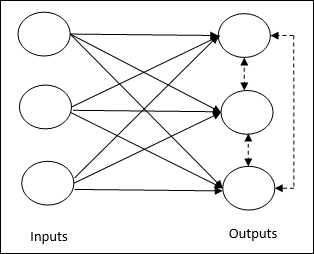
Basic Concept of Competitive Learning Rule− 앞서 언급했듯이 출력 노드간에 경쟁이있을 것입니다. 따라서 주요 개념은 훈련 중에 주어진 입력 패턴에 대해 가장 높은 활성화를 가진 출력 단위가 승자로 선언된다는 것입니다. 이 규칙을 Winner-takes-all이라고도합니다. 우승 한 뉴런 만 업데이트되고 나머지 뉴런은 변경되지 않기 때문입니다.

Mathematical formulation − 다음은이 학습 규칙의 수학적 공식화를위한 세 가지 중요한 요소입니다 −

Condition to be a winner − 뉴런 $ y_ {k} $ ⁡ ⁡이 승자가 되고자한다면 다음과 같은 조건이있을 것입니다. −

$$ y_ {k} \ : = \ : \ begin {cases} 1 & if \ : v_ {k} \ :> \ : v_ {j} \ : for \ : all \ : j, \ : j \ : \ neq \ : k \\ 0 및 기타 \ end {cases} $$

즉, $ y_ {k} $ ⁡과 같은 뉴런이 이기고 자하는 경우 유도 된 로컬 필드 (합산 단위의 출력) 인 $ v_ {k} $가 다른 모든 뉴런 중에서 가장 커야합니다. 네트워크에서.

Condition of sum total of weight − 경쟁 학습 규칙에 대한 또 다른 제약은 특정 출력 뉴런에 대한 가중치의 합계가 1이 될 것입니다. 예를 들어 뉴런을 고려한다면 k 다음-

$$ \ displaystyle \ sum \ limits_ {j} w_ {kj} \ : = \ : 1 \ : \ : \ : \ : \ : \ : \ : \ : \ : for \ : all \ : k $$

Change of weight for winner− 뉴런이 입력 패턴에 반응하지 않으면 해당 뉴런에서 학습이 이루어지지 않습니다. 그러나 특정 뉴런이 이기면 해당 가중치가 다음과 같이 조정됩니다.

$$ \ 델타 w_ {kj} \ : = \ : \ begin {cases}-\ alpha (x_ {j} \ :-\ : w_ {kj}), & if \ : neuron \ : k \ : wins \\ 0, & if \ : neuron \ : k \ : losses \ end {cases} $$

여기서 $ \ alpha $는 학습률입니다.

이것은 우리가 무게를 조정하여 승리하는 뉴런을 선호하고 있음을 분명히 보여 주며, 만약 뉴런이 손실되면 무게를 재조정 할 필요가 없습니다.