메모리 네트워크 연결
이러한 종류의 신경망은 패턴 연관을 기반으로 작동합니다. 즉, 서로 다른 패턴을 저장할 수 있으며 출력을 제공 할 때 지정된 입력 패턴과 일치시켜 저장된 패턴 중 하나를 생성 할 수 있습니다. 이러한 유형의 기억은Content-Addressable Memory(캠). 연관 메모리는 저장된 패턴을 데이터 파일로 사용하여 병렬 검색을 수행합니다.
다음은 우리가 관찰 할 수있는 두 가지 유형의 연관 기억입니다.
- 자동 연관 메모리
- 이종 연관 메모리
자동 연관 메모리
이것은 입력 훈련 벡터와 출력 대상 벡터가 동일한 단일 계층 신경망입니다. 가중치는 네트워크가 패턴 세트를 저장하도록 결정됩니다.
건축물
다음 그림과 같이 Auto Associative 메모리 네트워크의 아키텍처는 ‘n’ 입력 훈련 벡터 및 유사한 수 ‘n’ 출력 대상 벡터의 수.
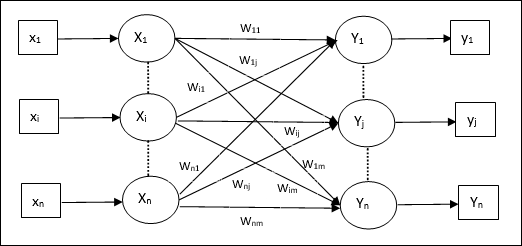
훈련 알고리즘
훈련을 위해이 네트워크는 Hebb 또는 Delta 학습 규칙을 사용합니다.
Step 1 − 다음과 같이 모든 가중치를 0으로 초기화합니다. wij = 0 (i = 1 to n, j = 1 to n)
Step 2 − 각 입력 벡터에 대해 3-4 단계를 수행합니다.
Step 3 − 다음과 같이 각 입력 장치를 활성화합니다 −
$$ x_ {i} \ : = \ : s_ {i} \ :( i \ : = \ : 1 \ : to \ : n) $$
Step 4 − 다음과 같이 각 출력 장치를 활성화합니다 −
$$ y_ {j} \ : = \ : s_ {j} \ :( j \ : = \ : 1 \ : to \ : n) $$
Step 5 − 다음과 같이 가중치를 조정합니다 −
$$ w_ {ij} (신규) \ : = \ : w_ {ij} (이전) \ : + \ : x_ {i} y_ {j} $$
테스트 알고리즘
Step 1 − Hebb의 규칙에 대해 훈련 중에 얻은 가중치를 설정합니다.
Step 2 − 각 입력 벡터에 대해 3-5 단계를 수행합니다.
Step 3 − 입력 벡터의 활성화와 동일하게 입력 단위의 활성화를 설정합니다.
Step 4 − 각 출력 장치에 대한 순 입력 계산 j = 1 to n
$$ y_ {inj} \ : = \ : \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$
Step 5 − 다음 활성화 함수를 적용하여 출력을 계산합니다.
$$ y_ {j} \ : = \ : f (y_ {inj}) \ : = \ : \ begin {cases} +1 & if \ : y_ {inj} \ :> \ : 0 \\-1 & if \ : y_ {inj} \ : \ leqslant \ : 0 \ end {cases} $$
이종 연관 메모리
Auto Associative Memory 네트워크와 유사하게 이것은 단일 레이어 신경망이기도합니다. 그러나이 네트워크에서 입력 훈련 벡터와 출력 대상 벡터는 동일하지 않습니다. 가중치는 네트워크가 패턴 세트를 저장하도록 결정됩니다. 이종 연관 네트워크는 본질적으로 정적이므로 비선형 및 지연 작업이 없습니다.
건축물
다음 그림과 같이 Hetero Associative Memory 네트워크의 아키텍처는 ‘n’ 입력 훈련 벡터 수 및 ‘m’ 출력 대상 벡터의 수.
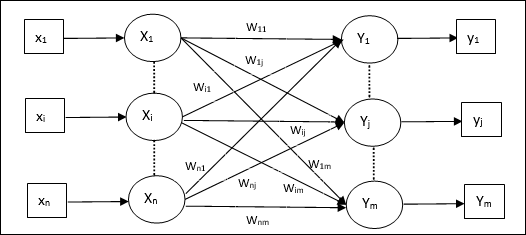
훈련 알고리즘
훈련을 위해이 네트워크는 Hebb 또는 Delta 학습 규칙을 사용합니다.
Step 1 − 다음과 같이 모든 가중치를 0으로 초기화합니다. wij = 0 (i = 1 to n, j = 1 to m)
Step 2 − 각 입력 벡터에 대해 3-4 단계를 수행합니다.
Step 3 − 다음과 같이 각 입력 장치를 활성화합니다 −
$$ x_ {i} \ : = \ : s_ {i} \ :( i \ : = \ : 1 \ : to \ : n) $$
Step 4 − 다음과 같이 각 출력 장치를 활성화합니다 −
$$ y_ {j} \ : = \ : s_ {j} \ :( j \ : = \ : 1 \ : to \ : m) $$
Step 5 − 다음과 같이 가중치를 조정합니다 −
$$ w_ {ij} (신규) \ : = \ : w_ {ij} (이전) \ : + \ : x_ {i} y_ {j} $$
테스트 알고리즘
Step 1 − Hebb의 규칙에 대해 훈련 중에 얻은 가중치를 설정합니다.
Step 2 − 각 입력 벡터에 대해 3-5 단계를 수행합니다.
Step 3 − 입력 벡터의 활성화와 동일하게 입력 단위의 활성화를 설정합니다.
Step 4 − 각 출력 장치에 대한 순 입력 계산 j = 1 to m;
$$ y_ {inj} \ : = \ : \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$
Step 5 − 다음 활성화 함수를 적용하여 출력을 계산합니다.
$$ y_ {j} \ : = \ : f (y_ {inj}) \ : = \ : \ begin {cases} +1 & if \ : y_ {inj} \ :> \ : 0 \\ 0 & if \ : y_ {inj} \ : = \ : 0 \\-1 & if \ : y_ {inj} \ : <\ : 0 \ end {cases} $$