DAA - Algorytm wspinaczki górskiej

Algorytmy omówione w poprzednich rozdziałach działają systematycznie. Aby osiągnąć cel, należy zapisać jedną lub więcej wcześniej zbadanych ścieżek prowadzących do rozwiązania, aby znaleźć optymalne rozwiązanie.

W przypadku wielu problemów droga do celu jest nieistotna. Na przykład w problemie N-Queens nie musimy przejmować się ostateczną konfiguracją hetmanów ani kolejnością dodawania hetmanów.

Wspinaczka górska

Wspinaczka górska to technika rozwiązywania pewnych problemów optymalizacyjnych. W tej technice zaczynamy od nieoptymalnego rozwiązania, a rozwiązanie jest wielokrotnie ulepszane, aż do zmaksymalizowania pewnego warunku.

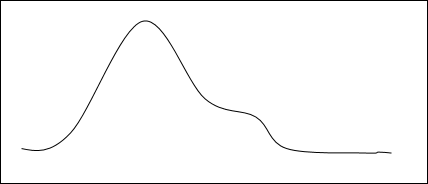
Pomysł rozpoczęcia od nieoptymalnego rozwiązania jest porównywany do rozpoczynania od podstawy wzgórza, ulepszanie rozwiązania jest porównywane do wchodzenia na wzgórze, a ostatecznie maksymalizacja pewnego stanu jest porównywana do dotarcia na szczyt wzgórza.

Dlatego technikę wspinaczki górskiej można rozpatrywać w następujących fazach -

• Konstruowanie nieoptymalnego rozwiązania uwzględniającego ograniczenia problemu
• Poprawianie rozwiązania krok po kroku
• Ulepszanie rozwiązania, aż nie będzie już możliwe

Technika wspinaczki górskiej jest używana głównie do rozwiązywania trudnych obliczeniowo problemów. Patrzy tylko na stan obecny i najbliższy stan przyszły. Dlatego ta technika jest wydajna pod względem pamięci, ponieważ nie obsługuje drzewa wyszukiwania.

Algorithm: Hill Climbing 
Evaluate the initial state. 
Loop until a solution is found or there are no new operators left to be applied: 
   - Select and apply a new operator 
   - Evaluate the new state: 
      goal -→ quit 
      better than current state -→ new current state

Iteracyjna poprawa

W iteracyjnej metodzie doskonalenia optymalne rozwiązanie osiąga się poprzez postęp w kierunku optymalnego rozwiązania w każdej iteracji. Jednak ta technika może napotkać lokalne maksima. W tej sytuacji nie ma w pobliżu stanu lepszego rozwiązania.

Tego problemu można uniknąć różnymi metodami. Jedną z tych metod jest symulowane wyżarzanie.

Losowe ponowne uruchomienie

To kolejna metoda rozwiązania problemu optymalizacji lokalnej. Ta technika przeprowadza serię poszukiwań. Za każdym razem zaczyna się od losowo wygenerowanego stanu początkowego. Stąd można uzyskać optymalne lub prawie optymalne rozwiązanie porównując rozwiązania przeprowadzonych poszukiwań.

Problemy techniki wspinaczki górskiej

Local Maxima

Jeśli heurystyka nie jest wypukła, Hill Climbing może zbiegać się do lokalnych maksimów zamiast globalnych maksimów.

Grzbiety i aleje

Jeśli funkcja celu tworzy wąski grzbiet, wówczas wspinacz może wejść na grzbiet lub zejść z alejki tylko zygzakiem. W tym scenariuszu wspinacz musi wykonać bardzo małe kroki, które wymagają więcej czasu, aby osiągnąć cel.

Płaskowyż

Plateau jest napotykane, gdy przestrzeń poszukiwań jest płaska lub dostatecznie płaska, że ​​wartość zwracana przez funkcję docelową jest nie do odróżnienia od wartości zwracanej dla pobliskich regionów, ze względu na precyzję używaną przez maszynę do reprezentowania jej wartości.

Złożoność techniki pokonywania wzniesień

Ta technika nie ma problemów związanych z przestrzenią, ponieważ dotyczy tylko obecnego stanu. Wcześniej zbadane ścieżki nie są zapisywane.

W przypadku większości problemów związanych z techniką wspinaczki pod górę z przypadkowym ponownym uruchomieniem optymalne rozwiązanie można osiągnąć w czasie wielomianowym. Jednak w przypadku problemów NP-Complete czas obliczeniowy może być wykładniczy w oparciu o liczbę lokalnych maksimów.

Zastosowania techniki wspinaczki górskiej

Technika wspinaczki górskiej może być wykorzystana do rozwiązania wielu problemów, w przypadku których obecny stan pozwala na dokładną ocenę funkcji, takich jak Network-Flow, problem Traveling Salesman, problem 8-Queens, projektowanie układów scalonych itp.

Wspinaczka górska jest również wykorzystywana w indukcyjnych metodach uczenia się. Technika ta jest używana w robotyce do koordynacji wielu robotów w zespole. Istnieje wiele innych problemów związanych z tą techniką.

Przykład

Technikę tę można zastosować do rozwiązania problemu komiwojażera. Najpierw ustalane jest wstępne rozwiązanie, które polega na odwiedzeniu wszystkich miast dokładnie raz. Stąd to początkowe rozwiązanie nie jest w większości przypadków optymalne. Nawet to rozwiązanie może być bardzo słabe. Algorytm Hill Climbing zaczyna się od takiego początkowego rozwiązania i wprowadza do niego iteracyjne ulepszenia. W końcu prawdopodobnie zostanie uzyskana znacznie krótsza trasa.