DAA - Vertex Cover

Pokrycie wierzchołka niekierunkowego grafu G = (V, E) jest podzbiorem wierzchołków V^' ⊆ V takie, że jeśli krawędź (u, v) jest krawędzią G, to albo u w V lub v w V^' lub obydwa.

Znajdź pokrycie wierzchołków o maksymalnym rozmiarze na podanym wykresie niekierowanym. To optymalne pokrycie wierzchołków jest optymalizacyjną wersją problemu NP-zupełnego. Jednak nie jest zbyt trudno znaleźć pokrycie wierzchołków, które jest bliskie optymalnej.

APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G] 
while E' is not empty do 
   Let (u, v) be an arbitrary edge of E' c ← c U {u, v} 
   Remove from E' every edge incident on either u or v 
return c

Przykład

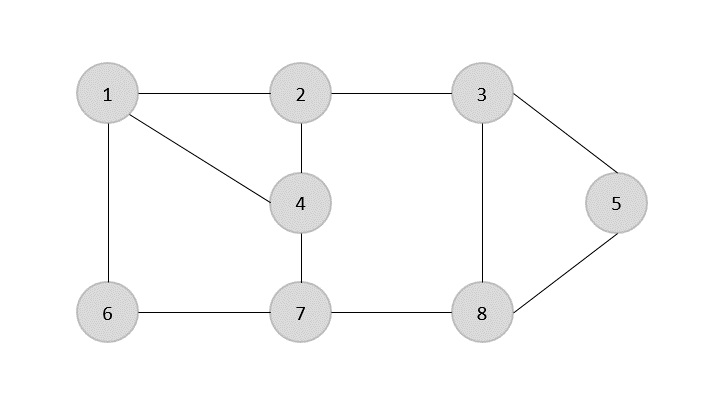
Zbiór krawędzi danego wykresu to -

{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}

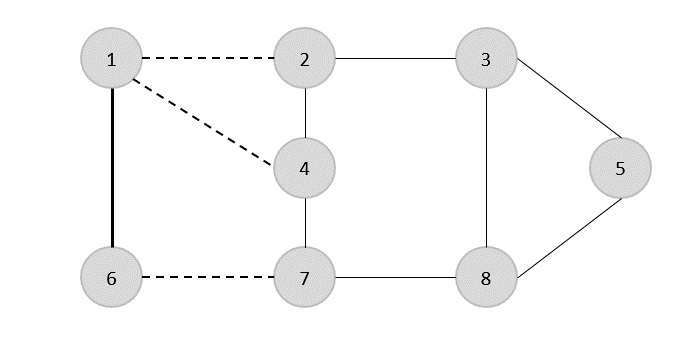
Teraz zaczynamy od wybrania dowolnej krawędzi (1,6). Eliminujemy wszystkie krawędzie, które padają na wierzchołek 1 lub 6 i dodajemy krawędź (1,6) do pokrycia.

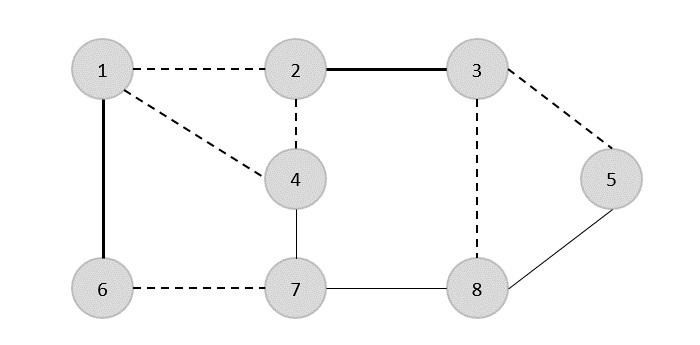
W następnym kroku wybraliśmy losowo kolejną krawędź (2,3)

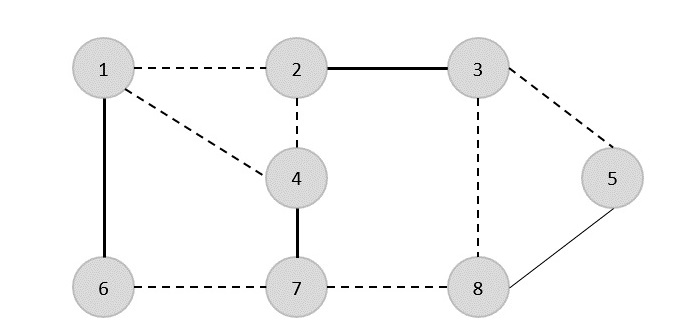
Teraz wybieramy inną krawędź (4,7).

Wybieramy inną krawędź (8,5).

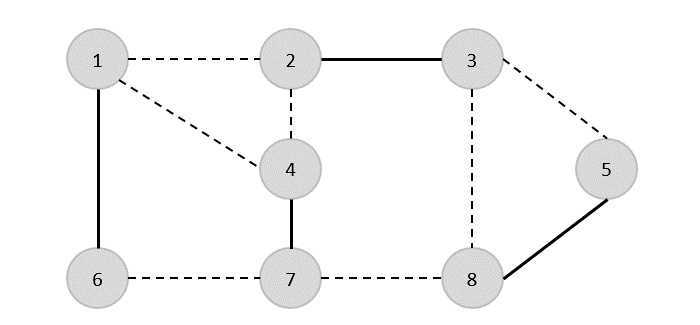
Stąd pokrycie wierzchołków tego wykresu wynosi {1, 2, 4, 5}.

Analiza

Łatwo zauważyć, że czas działania tego algorytmu to O(V + E), używając do reprezentowania listy sąsiedztwa E^'.