DAA - najdłuższa wspólna następstwo

Najdłuższym wspólnym problemem podciągów jest znalezienie najdłuższej sekwencji istniejącej w obu podanych łańcuchach.

Następstwo

Rozważmy ciąg S = <s ₁ , s ₂ , s ₃ , s ₄ ,…, s _n >.

Sekwencja Z = <z ₁ , z ₂ , z ₃ , z ₄ ,…, z _m > nad S nazywana jest podsekwencją S, wtedy i tylko wtedy, gdy można ją wyprowadzić z delecji S niektórych elementów.

Wspólna konsekwencja

Przypuszczać, X i Yto dwie sekwencje na skończonym zbiorze elementów. Możemy to powiedziećZ jest wspólnym następstwem X i Y, Jeśli Z jest podciągiem obu X i Y.

Najdłuższa wspólna kolejność

Jeśli podany jest zestaw sekwencji, najdłuższym wspólnym problemem podciągów jest znalezienie wspólnego podciągu wszystkich sekwencji o maksymalnej długości.

Najdłuższym wspólnym problemem podciągu jest klasyczny problem informatyczny, będący podstawą programów do porównywania danych, takich jak narzędzie diff, i znajduje zastosowanie w bioinformatyce. Jest również szeroko stosowany w systemach kontroli wersji, takich jak SVN i Git, do uzgadniania wielu zmian wprowadzonych w kolekcji plików z kontrolą wersji.

Metoda naiwna

Pozwolić X być sekwencją długości m i Y sekwencja długości n. Sprawdź każdy podciągX czy jest to podciąg Yi zwraca najdłuższy wspólny podciąg znaleziony.

Tam są 2^m podciągów X. Testowanie sekwencji bez względu na to, czy jest to podciągY trwa O(n)czas. W ten sposób przyjąłby naiwny algorytmO(n2^m) czas.

Programowanie dynamiczne

Niech X = <x ₁ , x ₂ , x ₃ ,…, x _m > i Y = <y ₁ , y ₂ , y ₃ ,…, y _n > będą sekwencjami. Do obliczenia długości elementu używany jest następujący algorytm.

W tej procedurze tabela C[m, n] jest obliczana w kolejności głównej wiersza i innej tabeli B[m,n] jest obliczana w celu skonstruowania optymalnego rozwiązania.

Algorithm: LCS-Length-Table-Formulation (X, Y)
m := length(X) 
n := length(Y) 
for i = 1 to m do 
   C[i, 0] := 0 
for j = 1 to n do 
   C[0, j] := 0 
for i = 1 to m do 
   for j = 1 to n do 
      if xi = yj 
         C[i, j] := C[i - 1, j - 1] + 1 
         B[i, j] := ‘D’ 
      else 
         if C[i -1, j] ≥ C[i, j -1] 
            C[i, j] := C[i - 1, j] + 1 
            B[i, j] := ‘U’ 
         else 
         C[i, j] := C[i, j - 1]
         B[i, j] := ‘L’ 
return C and B

Algorithm: Print-LCS (B, X, i, j)
if i = 0 and j = 0 
   return  
if B[i, j] = ‘D’ 
   Print-LCS(B, X, i-1, j-1) 
   Print(xi) 
else if B[i, j] = ‘U’ 
   Print-LCS(B, X, i-1, j) 
else 
   Print-LCS(B, X, i, j-1)

Ten algorytm wypisze najdłuższy wspólny podciąg X i Y.

Analiza

Aby wypełnić tabelę, plik zewnętrzny for pętla iteruje m czasy i wewnętrzne for pętla iteruje nczasy. Stąd złożoność algorytmu wynosi O (m, n) , gdziem i n to długość dwóch strun.

Przykład

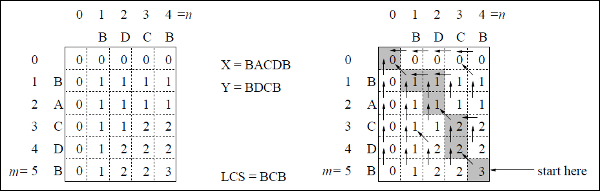
W tym przykładzie mamy dwa ciągi X = BACDB i Y = BDCB znaleźć najdłuższy wspólny podciąg.

Zgodnie z algorytmem LCS-Length-Table-Formulation (jak podano powyżej), obliczyliśmy tabelę C (pokazaną po lewej stronie) i tabelę B (pokazaną po prawej stronie).

W tabeli B zamiast „D”, „L” i „U” używamy odpowiednio strzałki ukośnej, strzałki w lewo i strzałki w górę. Po wygenerowaniu tabeli B LCS jest określane przez funkcję LCS-Print. Wynik to BCB.