DAA - optymalny wzór scalania
Scal zbiór posortowanych plików o różnej długości w jeden posortowany plik. Musimy znaleźć optymalne rozwiązanie, w którym wynikowy plik zostanie wygenerowany w minimalnym czasie.
Jeśli podano liczbę posortowanych plików, istnieje wiele sposobów na połączenie ich w jeden posortowany plik. To połączenie można przeprowadzić parami. Dlatego ten typ scalania nazywany jest as2-way merge patterns.
Ponieważ różne pary wymagają różnej ilości czasu, w tej strategii chcemy określić optymalny sposób łączenia wielu plików razem. Na każdym kroku łączone są dwie najkrótsze sekwencje.
Aby połączyć plik p-record file i a q-record file wymaga ewentualnie p + q nagrywanie ruchów, a oczywistym wyborem jest połączenie dwóch najmniejszych plików razem na każdym kroku.
Wzorce scalania dwukierunkowego mogą być reprezentowane przez binarne drzewa scalania. Rozważmy zbiórn posortowane pliki {f1, f2, f3, …, fn}. Początkowo każdy element tego jest traktowany jako drzewo binarne z pojedynczym węzłem. Aby znaleźć to optymalne rozwiązanie, używany jest następujący algorytm.
Algorithm: TREE (n)
for i := 1 to n – 1 do
declare new node
node.leftchild := least (list)
node.rightchild := least (list)
node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)
insert (list, node);
return least (list);Na końcu tego algorytmu waga węzła głównego reprezentuje optymalny koszt.
Przykład
Rozważmy podane pliki, f 1 , f 2 , f 3 , f 4 if 5 z odpowiednio 20, 30, 10, 5 i 30 liczbą elementów.
Jeśli operacje scalania są wykonywane zgodnie z podaną sekwencją, to
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Stąd całkowita liczba operacji wynosi
50 + 60 + 65 + 95 = 270
Powstaje pytanie, czy istnieje lepsze rozwiązanie?
Sortując liczby według ich rozmiaru w porządku rosnącym, otrzymujemy następującą sekwencję -
f4, f3, f1, f2, f5
W związku z tym operacje łączenia mogą być wykonywane na tej sekwencji
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Dlatego całkowita liczba operacji wynosi
15 + 35 + 65 + 95 = 210
Oczywiście jest to lepsze niż poprzednie.
W tym kontekście zamierzamy teraz rozwiązać problem za pomocą tego algorytmu.
Zestaw początkowy

Krok 1
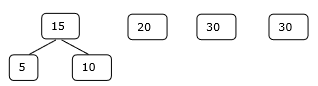
Krok 2
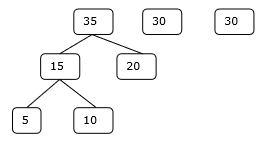
Krok 3
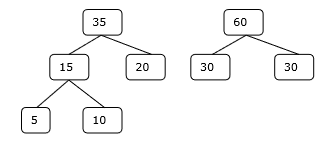
Krok 4
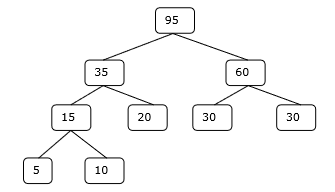
Stąd rozwiązanie wymaga 15 + 35 + 60 + 95 = 205 ilości porównań.