Klasy twarde i NP-kompletne
Problem występuje w NPC klasy, jeśli jest w NP i jest taki sam hardjak każdy problem w NP. Problem w tymNP-hard jeśli wszystkie problemy w NP można zredukować do czasu wielomianu, nawet jeśli nie jest w samym NP.
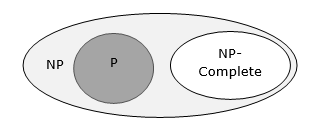
Jeśli dla któregokolwiek z tych problemów istnieje algorytm czasu wielomianowego, wszystkie problemy w NP można by rozwiązać w czasie wielomianowym. Te problemy są nazywaneNP-complete. Zjawisko NP-zupełności jest ważne zarówno ze względów teoretycznych, jak i praktycznych.
Definicja kompletności NP
Język B jest NP-complete jeśli spełnia dwa warunki
B jest w NP
Każdy A w NP jest czas wielomianowy redukowalny do B.
Jeśli język spełnia drugą właściwość, ale niekoniecznie pierwszą, język B jest znany jako NP-Hard. Nieformalnie, problem z wyszukiwaniemB jest NP-Hard jeśli istnieje NP-Complete problem A do której Turing redukuje B.
Problem w NP-Hard nie może być rozwiązany w czasie wielomianowym, dopóki P = NP. Jeśli okaże się, że problemem jest NPC, nie ma potrzeby tracić czasu na szukanie wydajnego algorytmu. Zamiast tego możemy skupić się na algorytmie aproksymacji projektu.
Problemy NP-Complete
Poniżej przedstawiono kilka problemów NP-Complete, dla których nie jest znany algorytm czasu wielomianowego.
- Określenie, czy wykres ma cykl Hamiltona
- Ustalenie, czy formuła boolowska jest satysfakcjonująca itp.
NP-trudne problemy
Następujące problemy są NP-trudne
- Problem zgodności obwodu
- Ustaw osłonę
- Pokrywa wierzchołków
- Problem komiwojażera
W tym kontekście omówimy teraz TSP jest NP-Complete
TSP jest NP-Complete
Problem komiwojażera składa się z komiwojażera i zbioru miast. Sprzedawca musi odwiedzić każde z miast, zaczynając od określonego i wracając do tego samego miasta. Problem polega na tym, że komiwojażer chce zminimalizować całkowitą długość podróży
Dowód
Udowodnić TSP is NP-Complete, najpierw musimy to udowodnić TSP belongs to NP. W TSP znajdujemy wycieczkę i sprawdzamy, czy trasa zawiera jeden wierzchołek. Następnie obliczany jest całkowity koszt krawędzi trasy. Na koniec sprawdzamy, czy koszt jest minimalny. Można to wykonać w czasie wielomianowym. A zatemTSP belongs to NP.
Po drugie, musimy to udowodnić TSP is NP-hard. Aby to udowodnić, jednym ze sposobów jest pokazanie tegoHamiltonian cycle ≤p TSP (jak wiemy, że problem cyklu Hamiltona jest NPkompletny).
Założyć G = (V, E) być przykładem cyklu Hamiltona.
W związku z tym konstruowana jest instancja TSP. Tworzymy pełny wykresG' = (V, E'), gdzie
$$ E ^ {'} = \ lbrace (i, j) \ colon i, j \ in V \: \: and \: i \ neq j $$
Zatem funkcja kosztu jest zdefiniowana w następujący sposób -
$$ t (i, j) = \ begin {cases} 0 & if \: (i, j) \: \ in E \\ 1 & w przeciwnym razie \ end {cases} $$
Teraz przypuśćmy, że cykl Hamiltona h istnieje w G. Oczywiste jest, że koszt każdej krawędzi wh jest 0 w G' do której należy każda krawędź E. W związku z tym,h ma koszt 0 w G'. Tak więc, jeśli wykresG ma cykl Hamiltona, a następnie wykres G' ma wycieczkę po 0 koszt.
I odwrotnie, zakładamy, że G' ma wycieczkę h' kosztu najwyżej 0. Koszt krawędzi wE' są 0 i 1zgodnie z definicją. Dlatego każda krawędź musi mieć koszt0 jako koszt h' jest 0. Dlatego wyciągamy z tego wniosekh' zawiera tylko krawędzie w E.
W ten sposób udowodniliśmy to G ma cykl Hamiltona, wtedy i tylko wtedy, gdy G' kosztuje co najwyżej wycieczkę 0. TSP jest NP-kompletny.