DAA - najkrótsze ścieżki

Algorytm Dijkstry

Algorytm Dijkstry rozwiązuje problem najkrótszych ścieżek z jednym źródłem na ukierunkowanym grafie ważonym G = (V, E) , gdzie wszystkie krawędzie są nieujemne (tj. W (u, v) ≥ 0 dla każdej krawędzi (u, v ) Є E ).

W poniższym algorytmie użyjemy jednej funkcji Extract-Min(), który wyodrębnia węzeł za pomocą najmniejszego klucza.

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

Analiza

Złożoność tego algorytmu jest w pełni zależna od implementacji funkcji Extract-Min. Jeśli funkcja wyodrębniania min jest zaimplementowana przy użyciu wyszukiwania liniowego, złożoność tego algorytmu wynosiO(V² + E).

W tym algorytmie, jeśli użyjemy min-sterty na której Extract-Min() funkcja działa, aby zwrócić węzeł z Q najmniejszym kluczem można jeszcze bardziej zmniejszyć złożoność tego algorytmu.

Przykład

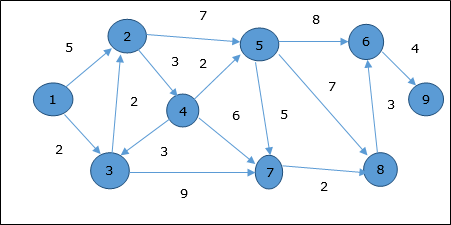
Rozważmy wierzchołek 1 i 9odpowiednio jako wierzchołek początkowy i docelowy. Początkowo wszystkie wierzchołki oprócz wierzchołka początkowego są oznaczone przez ∞, a wierzchołek początkowy jest oznaczony przez0.

Wierzchołek	Inicjał	Krok 1 V 1	Krok 2 V 3	Krok 3 V 2	Krok 4 V 4	Krok 5 V 5	Krok 6 V 7	Krok 7 V 8	Step8 V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
3	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	7	7	7	7	7	7
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
7	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

Stąd minimalna odległość wierzchołka 9 od wierzchołka 1 jest 20. A ścieżka jest

1 → 3 → 7 → 8 → 6 → 9

Ta ścieżka jest określana na podstawie informacji o poprzedniku.

Algorytm Bellmana Forda

Ten algorytm rozwiązuje problem najkrótszej ścieżki z jednego źródła w grafie skierowanym G = (V, E)w którym wagi krawędzi mogą być ujemne. Co więcej, algorytm ten można zastosować do znalezienia najkrótszej ścieżki, jeśli nie istnieje żaden cykl ważony ujemnie.

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

Analiza

Pierwszy for pętla jest używana do inicjalizacji, która działa w O(V)czasy. Następnyfor działa pętla |V - 1| przechodzi przez krawędzie, które trwaO(E) czasy.

W związku z tym działa algorytm Bellmana-Forda O(V, E) czas.

Przykład

Poniższy przykład pokazuje krok po kroku, jak działa algorytm Bellmana-Forda. Ten wykres ma ujemną krawędź, ale nie ma żadnego ujemnego cyklu, dlatego problem można rozwiązać za pomocą tej techniki.

W momencie inicjalizacji wszystkie wierzchołki oprócz źródła są oznaczone przez ∞, a źródło jest oznaczone przez 0.

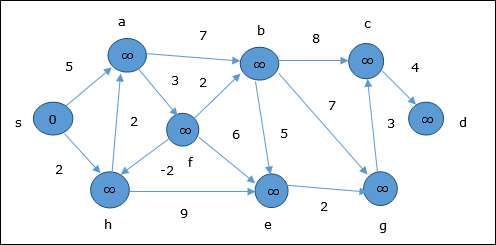
W pierwszym kroku wszystkie wierzchołki, do których można dotrzeć ze źródła, są aktualizowane przy minimalnym koszcie. Stąd wierzchołkia i h są aktualizowane.

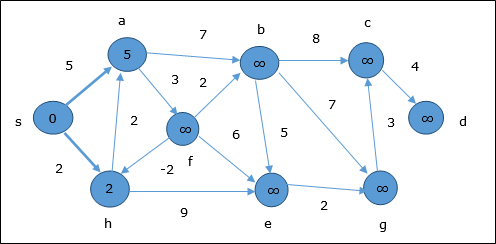
W następnym kroku wierzchołki a, b, f i e są aktualizowane.

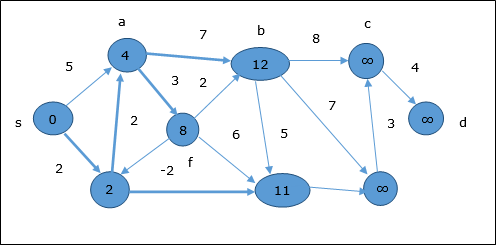
Zgodnie z tą samą logiką, w tym kroku wierzchołki b, f, c i g są aktualizowane.

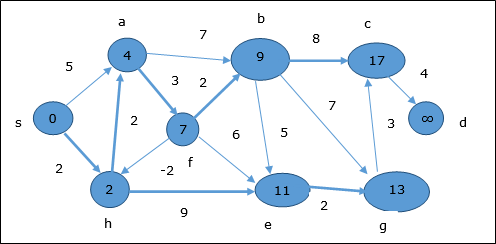
Tutaj wierzchołki c i d są aktualizowane.

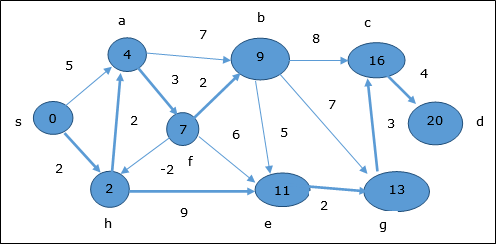
Stąd minimalna odległość między wierzchołkami s i wierzchołek d jest 20.

Opierając się na poprzednich informacjach, ścieżka to s → h → e → g → c → d