DAA - Spanning Tree

ZA spanning tree jest podzbiorem niekierowanego Grafu, który ma wszystkie wierzchołki połączone minimalną liczbą krawędzi.

Jeśli wszystkie wierzchołki są połączone w grafie, istnieje co najmniej jedno drzewo opinające. Na wykresie może istnieć więcej niż jedno drzewo opinające.

Nieruchomości

Drzewo opinające nie ma żadnego cyklu.
Do każdego wierzchołka można dotrzeć z dowolnego innego wierzchołka.

Przykład

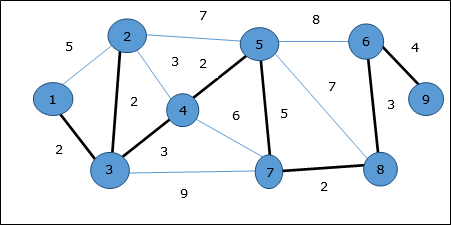
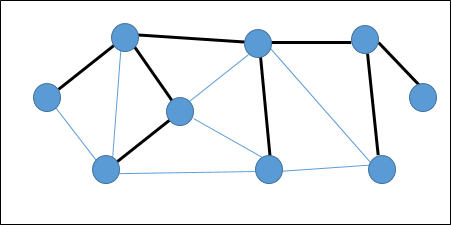
Na poniższym wykresie podświetlone krawędzie tworzą drzewo opinające.

Minimalne drzewo rozpinające

ZA Minimum Spanning Tree (MST)jest podzbiorem krawędzi połączonego ważonego grafu niekierowanego, który łączy wszystkie wierzchołki razem z minimalną możliwą całkowitą wagą krawędzi. Aby uzyskać MST, można użyć algorytmu Prima lub algorytmu Kruskala. Dlatego w tym rozdziale omówimy algorytm Prim.

Jak omówiliśmy, jeden wykres może mieć więcej niż jedno drzewo opinające. Jeśli tam sąn liczba wierzchołków, jaką powinno mieć drzewo opinające n - 1liczba krawędzi. W tym kontekście, jeśli każda krawędź wykresu jest powiązana z wagą i istnieje więcej niż jedno drzewo opinające, musimy znaleźć minimalne drzewo opinające wykresu.

Ponadto, jeśli istnieją zduplikowane krawędzie ważone, wykres może mieć wiele minimalnych drzew rozpinających.

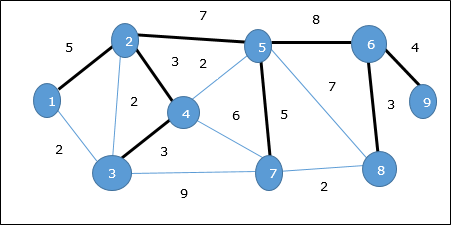
Na powyższym wykresie pokazaliśmy drzewo opinające, chociaż nie jest to minimalne drzewo opinające. Koszt tego drzewa rozpinającego wynosi (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38.

Użyjemy algorytmu Prim do znalezienia minimalnego drzewa opinającego.

Algorytm Prima

Algorytm Prim jest zachłannym podejściem do znalezienia minimalnego drzewa opinającego. W tym algorytmie, aby utworzyć MST, możemy zacząć od dowolnego wierzchołka.

Algorithm: MST-Prim’s (G, w, r) 
for each u є G.V 
   u.key = ∞ 
   u.∏ = NIL 
r.key = 0 
Q = G.V 
while Q ≠ Ф 
   u = Extract-Min (Q) 
   for each v є G.adj[u] 
      if each v є Q and w(u, v) < v.key 
         v.∏ = u 
         v.key = w(u, v)

Funkcja Extract-Min zwraca wierzchołek z minimalnym kosztem krawędzi. Ta funkcja działa na min-sterty.

Przykład

Korzystając z algorytmu Prima, możemy zacząć od dowolnego wierzchołka, zacznijmy od wierzchołka 1.

Wierzchołek 3 jest połączony z wierzchołkiem 1 przy minimalnych kosztach krawędzi, a tym samym przewaga (1, 2) jest dodawany do drzewa opinającego.

Następnie krawędź (2, 3) jest uważane, ponieważ jest to minimum między krawędziami {(1, 2), (2, 3), (3, 4), (3, 7)}.

W następnym kroku otrzymujemy przewagę (3, 4) i (2, 4)przy minimalnych kosztach. Brzeg(3, 4) jest wybierany losowo.

W podobny sposób krawędzie (4, 5), (5, 7), (7, 8), (6, 8) i (6, 9)są wybrane. Ponieważ wszystkie wierzchołki są odwiedzane, algorytm się zatrzymuje.

Koszt drzewa opinającego wynosi (2 + 2 + 3 + 2 + 5 + 2 + 3 + 4) = 23. Na tym wykresie nie ma więcej drzewa opinającego o koszcie mniejszym niż 23.