Techniki regresji
Regresja to technika statystyczna, która pomaga w określeniu związku między powiązanymi ze sobą zmiennymi ekonomicznymi. Pierwszy krok polega na oszacowaniu współczynnika zmiennej niezależnej, a następnie pomiarze rzetelności oszacowanego współczynnika. Wymaga to sformułowania hipotezy, a na jej podstawie możemy stworzyć funkcję.
Jeśli menedżer chce określić zależność między wydatkami na reklamę firmy a jej przychodami ze sprzedaży, poddaje się testowi hipotezy. Zakładając, że wyższe wydatki na reklamę prowadzą do wyższej sprzedaży dla firmy. Menedżer zbiera dane o wydatkach na reklamę oraz o przychodach ze sprzedaży w określonym czasie. Hipotezę tę można przełożyć na funkcję matematyczną, gdzie prowadzi do -
Y = A + Bx
Gdzie Y to sprzedaż, x to wydatki na reklamę, A i B są stałe.
Po przełożeniu hipotezy na funkcję, podstawą tego jest znalezienie związku między zmienną zależną i niezależną. Wartość zmiennej zależnej ma największe znaczenie dla badaczy i zależy od wartości innych zmiennych. Zmienna niezależna służy do wyjaśnienia zmienności zmiennej zależnej. Można go podzielić na dwa typy -
Simple regression - Jedna zmienna niezależna
Multiple regression - Kilka zmiennych niezależnych
Prosta regresja
Poniżej przedstawiono kroki prowadzące do opracowania analizy regresji -
- Określ model regresji
- Uzyskaj dane o zmiennych
- Oszacuj zależności ilościowe
- Przetestuj znaczenie statystyczne wyników
- Wykorzystanie wyników w podejmowaniu decyzji
Wzór na prostą regresję to -
Y = a + bX + u
Y= zmienna zależna
X= zmienna niezależna
a= punkt przecięcia z osią
b= nachylenie
u= czynnik losowy
Dane przekrojowe dostarczają informacji o grupie podmiotów w danym czasie, natomiast dane szeregów czasowych dostarczają informacji o jednym obiekcie w czasie. Kiedy szacujemy równanie regresji, obejmuje to proces znajdowania najlepszej zależności liniowej między zmiennymi zależnymi i niezależnymi.
Metoda zwykłych najmniejszych kwadratów (OLS)
Zwykła metoda najmniejszych kwadratów jest zaprojektowana tak, aby dopasować linię przez rozrzut punktów w taki sposób, aby zminimalizować sumę kwadratów odchyleń punktów od linii. Jest to metoda statystyczna. Zwykle pakiety oprogramowania wykonują oszacowanie OLS.
Y = a + bX
Współczynnik Oznaczania (R 2 )
Współczynnik określania jest miarą, która wskazuje procent zmienności zmiennej zależnej wynikający z wahań zmiennych niezależnych. R 2 jest miarą dobroci dopasowania modelu. Oto metody -
Całkowita suma kwadratów (TSS)
Suma kwadratów odchyleń wartości próbki Y od średniej Y.
TSS = SUM ( Yi − Y)2
Yi = zmienne zależne
Y = średnia zmiennych zależnych
i = liczba obserwacji
Regresja sumy kwadratów (RSS)
Suma kwadratów odchyleń oszacowanych wartości Y od średniej Y.
RSS = SUM ( Ỷi − uY)2
Ỷi = szacunkowa wartość Y
Y = średnia zmiennych zależnych
i = liczba odmian
Błąd sumy kwadratów (ESS)
Suma kwadratów odchyleń wartości próbki Y od oszacowanych wartości Y.
ESS = SUM ( Yi − Ỷi)2
Ỷi = szacunkowa wartość Y
Yi = zmienne zależne
i = liczba obserwacji
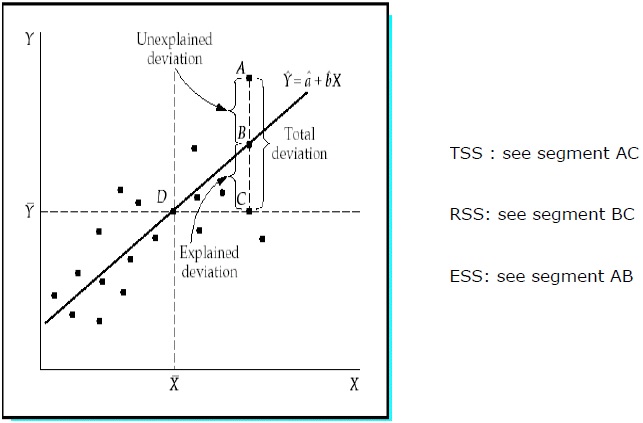
R 2 mierzy odsetek całkowitego odchylenia Y od jego średniej, co wyjaśnia model regresji. Im bliżej jedności R 2 , tym większa moc wyjaśniająca równania regresji. R 2 bliskie 0 oznacza, że równanie regresji będzie miało bardzo małą moc wyjaśniającą.
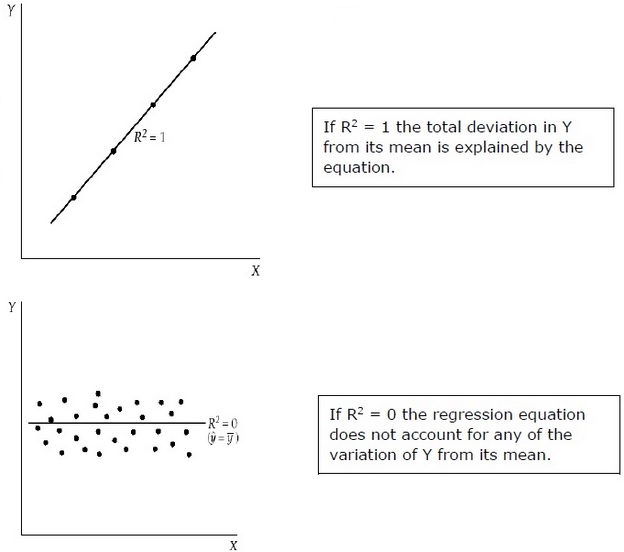
Do oceny współczynników regresji używana jest próba z populacji, a nie cała populacja. Ważne jest, aby przyjąć założenia dotyczące populacji na podstawie próby i dokonać oceny, jak dobre są te założenia.
Ocena współczynników regresji
Każda próbka z populacji generuje własny punkt przecięcia z osią. Aby obliczyć różnicę statystyczną, można zastosować następujące metody -
Two tailed test −
Hipoteza zerowa: H 0 : b = 0
Hipoteza alternatywna: H a : b ≠ 0
One tailed test −
Hipoteza zerowa: H 0 : b> 0 (lub b <0)
Hipoteza alternatywna: H a : b <0 (lub b> 0)
Statistic Test −
b = szacowany współczynnik
E (b) = b = 0 (hipoteza zerowa)
SE b = błąd standardowy współczynnika
.Wartość tzależy od stopnia swobody, jednego lub dwóch niezaliczonych testów i poziomu istotności. Aby określić krytyczną wartośćt, można użyć stołu t. Następnie następuje porównanie wartości t z wartością krytyczną. Należy odrzucić hipotezę zerową, jeśli bezwzględna wartość testu statystycznego jest większa lub równa krytycznej wartości t. Nie odrzucaj hipotezy zerowej, I bezwzględna wartość testu statystycznego jest mniejsza niż krytyczna wartość t.
Analiza regresji wielokrotnej
W przeciwieństwie do prostej regresji w analizie regresji wielorakiej współczynniki wskazują zmianę zmiennych zależnych przy założeniu, że wartości innych zmiennych są stałe.
Nazywa się test istotności statystycznej F-test. Test F jest przydatny, ponieważ mierzy istotność statystyczną całego równania regresji, a nie tylko dla osoby. Tutaj W hipotezie zerowej nie ma związku między zmienną zależną a zmiennymi niezależnymi populacji.
Wzór to - H 0 : b1 = b2 = b3 =…. = bk = 0
Nie ma związku między zmienną zależną a k zmienne niezależne dla populacji.
F-test static −
$$ F \: = \: \ frac {\ left (\ frac {R ^ 2} {K} \ right)} {\ frac {(1-R ^ 2)} {(nk-1)}} $$
Wartość krytyczna Fzależy od licznika i mianownika stopnia swobody i poziomu istotności. Do określenia krytycznej wartości F. można użyć tabeli F. W porównaniu z wartością F z wartością krytyczną (F *) -
Jeśli F> F *, musimy odrzucić hipotezę zerową.
Jeśli F <F *, nie odrzucaj hipotezy zerowej, ponieważ nie ma istotnego związku między zmienną zależną a wszystkimi zmiennymi niezależnymi.