Faktoryzacja podstawowa
Factors to liczby, które mnożymy, aby otrzymać kolejną liczbę.
Dla examplewspółczynniki 14 wynoszą 2 i 7, ponieważ 2 × 7 = 14.
Niektóre liczby można uwzględnić na więcej niż jeden sposób.
Dla example, 16 można rozłożyć na czynniki 1 × 16, 2 × 8 lub 4 × 4.
Liczba, którą można rozliczyć tylko jako 1 razy, nazywa się a prime number.
Kilka pierwszych liczb pierwszych to 2, 3, 5, 7, 11 i 13.
Nazywane są liczby, które mają wiele czynników composite numbers.
Liczba 1 nie jest ani liczbą pierwszą, ani złożoną.
Możemy zapisać dowolną liczbę całkowitą jako iloczyn dwóch czynników i rozpocząć a factor tree. Czynniki są dalej dzielone na swoje czynniki, aż pozostaną nam tylko czynniki pierwsze, których nie można dalej rozłożyć.
Najczęściej musisz znaleźć plik prime factors liczby: lista wszystkich czynników liczb pierwszych danej liczby.
Rozkład liczby na czynniki pierwsze i wyrażenie liczby jako iloczynu jej czynników pierwszych jest znane jako prime factorization tej liczby.
Plik prime factorization of a number obejmuje TYLKO czynniki pierwsze, a nie iloczyn tych czynników pierwszych.
Example
Znajdź czynniki pierwsze liczby 24
Rozwiązanie
Step 1:
Aby znaleźć czynniki pierwsze liczby 24, należy podzielić ją przez najmniejszą liczbę pierwszą, która dzieli ją równo: 24 ÷ 2 = 12.
Step 2:
Teraz podziel 12 przez najmniejszą liczbę pierwszą, która dzieli się równo: 12 ÷ 2 = 6.
Step 3:
Teraz podziel 6 przez najmniejszą liczbę pierwszą, która dzieli ją równo: 6 ÷ 2 = 3.
Step 4:
Ponieważ 3 jest liczbą pierwszą, faktoring jest zakończony, a pierwszy faktoryzacja 24 wynosi 2 × 2 × 2 × 3.
Znajdź wszystkie czynniki pierwsze liczby 48.
Rozwiązanie
Step 1:
Możemy podzielić 48 na jego czynniki, jak pokazano poniżej.
48 = 3 x 16;
16 = 2 x 8;
8 = 2 × 4;
4 = 2 × 2.
Step 2:
Drzewo czynników, które tu otrzymujemy, pokazano poniżej.
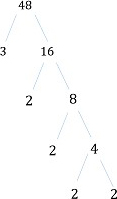
Step 3:
Czyli 48 zapisywane jako iloczyn jego czynników pierwszych lub faktoryzacji głównej 48 jest
48 = 2 × 2 × 2 × 2 × 3
Znajdź wszystkie czynniki pierwsze 75.
Rozwiązanie
Step 1:
Możemy podzielić 75 na jego czynniki, jak pokazano poniżej.
75 = 3 x 25;
25 = 5 × 5;
Step 2:
Drzewo czynników, które tu otrzymujemy, pokazano poniżej.
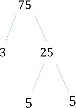
Step 3:
Czyli 75 zapisywane jako iloczyn jego czynników pierwszych lub pierwszego faktoryzacji 75 jest
75 = 3 × 5 × 5