Comunicação Analógica - Guia Rápido

A palavra comunicação surge da palavra latina commūnicāre, que significa “compartilhar”. A comunicação é a etapa básica para a troca de informações.

Por exemplo, um bebê no berço se comunica chorando quando precisa da mãe. Uma vaca muge alto quando está em perigo. Uma pessoa se comunica com a ajuda de um idioma. A comunicação é a ponte para compartilhar.

Communication pode ser definido como o processo de troca de informações por meios como palavras, ações, signos, etc., entre dois ou mais indivíduos.

Partes de um sistema de comunicação

Qualquer sistema que forneça comunicação consiste em três partes importantes e básicas, conforme mostrado na figura a seguir.

• Senderé a pessoa que envia a mensagem. Pode ser uma estação transmissora de onde o sinal é transmitido.

• Channel é o meio pelo qual os sinais de mensagem viajam para chegar ao destino.

• Receiveré a pessoa que recebe a mensagem. Pode ser uma estação receptora onde o sinal transmitido está sendo recebido.

Tipos de Sinais

Transmitir uma informação por alguns meios, como gestos, sons, ações, etc., pode ser denominado como signaling. Portanto, um sinal pode ser uma fonte de energia que transmite algumas informações. Este sinal ajuda a estabelecer uma comunicação entre o emissor e o receptor.

Um impulso elétrico ou uma onda eletromagnética que viaja uma distância para transmitir uma mensagem pode ser denominado como um signal em sistemas de comunicação.

Dependendo de suas características, os sinais são classificados principalmente em dois tipos: Analógico e Digital. Os sinais analógicos e digitais são classificados posteriormente, conforme mostrado na figura a seguir.

Sinal analógico

Um sinal de variação contínua no tempo, que representa uma quantidade variável no tempo, pode ser denominado como um Analog Signal. Este sinal continua variando com o tempo, de acordo com os valores instantâneos da grandeza que o representa.

Exemplo

Consideremos uma torneira que enche um tanque de 100 litros de capacidade em uma hora (6h às 7h). A porção de enchimento do tanque varia de acordo com o tempo. O que significa que, após 15 minutos (6h15), a porção de um quarto do tanque fica cheia, enquanto às 6h45, 3/4 do tanque está cheio.

Se tentarmos representar graficamente as porções variáveis ​​de água no tanque de acordo com o tempo variável, ficaria parecido com a figura a seguir.

Como o resultado mostrado nesta imagem varia (aumenta) com o tempo, este time varying quantitypode ser entendido como quantidade analógica. O sinal que representa esta condição com uma linha inclinada na figura, é umAnalog Signal. A comunicação baseada em sinais analógicos e valores analógicos é chamada deAnalog Communication.

Sinal digital

Um sinal que é discreto por natureza ou que não é contínuo em forma pode ser denominado como um Digital signal. Este sinal possui valores individuais, denotados separadamente, que não são baseados nos valores anteriores, como se fossem derivados naquele determinado instante de tempo.

Exemplo

Vamos considerar uma sala de aula com 20 alunos. Se o comparecimento deles em uma semana for plotado, seria semelhante à figura a seguir.

Nesta figura, os valores são indicados separadamente. Por exemplo, a assiduidade da aula na quarta-feira é de 20 e no sábado é de 15. Estes valores podem ser considerados individual e separadamente ou discretamente, por isso são chamadosdiscrete values.

Os dígitos binários que têm apenas 1s e 0s são geralmente denominados como digital values. Portanto, os sinais que representam 1s e 0s também são chamados dedigital signals. A comunicação baseada em sinais digitais e valores digitais é chamada deDigital Communication.

Sinal Periódico

Qualquer sinal analógico ou digital, que repete seu padrão ao longo de um período de tempo, é chamado de Periodic Signal. Este sinal tem seu padrão continuado repetidamente e é fácil de ser assumido ou calculado.

Exemplo

Se considerarmos uma máquina em uma indústria, o processo que ocorre um após o outro é um processo contínuo. Por exemplo, adquirir e classificar a matéria-prima, processar o material em lotes, embalar uma carga de produtos um após o outro, etc., segue um determinado procedimento repetidamente.

Tal processo, seja considerado analógico ou digital, pode ser representado graficamente como segue.

Sinal Aperiódico

Qualquer sinal analógico ou digital, que não repete seu padrão durante um período de tempo, é chamado de Aperiodic Signal. Este sinal tem seu padrão continuado, mas o padrão não se repete. Também não é tão fácil ser assumido ou calculado.

Exemplo

A rotina diária de uma pessoa, se considerada, consiste em vários tipos de trabalho que levam diferentes intervalos de tempo para diferentes tarefas. O intervalo de tempo ou o trabalho não se repete continuamente. Por exemplo, uma pessoa não vai escovar os dentes continuamente de manhã à noite, isso também com o mesmo período de tempo.

Tal processo, seja considerado analógico ou digital, pode ser representado graficamente como segue.

Em geral, os sinais que são usados ​​em sistemas de comunicação são de natureza analógica, que são transmitidos em analógico ou convertidos em digital e então transmitidos, dependendo da necessidade.

Para que um sinal seja transmitido à distância, sem o efeito de quaisquer interferências externas ou adição de ruídos e sem desaparecer, ele deve passar por um processo chamado Modulation. Ele melhora a intensidade do sinal sem perturbar os parâmetros do sinal original.

O que é modulação?

Uma mensagem com um sinal deve ser transmitida à distância e, para estabelecer uma comunicação confiável, precisa da ajuda de um sinal de alta frequência que não deve afetar as características originais do sinal de mensagem.

As características do sinal de mensagem, se alteradas, a mensagem nele contida também se altera. Portanto, é necessário cuidar do sinal de mensagem. Um sinal de alta freqüência pode viajar até uma distância maior, sem ser afetado por distúrbios externos. Temos a ajuda desse sinal de alta frequência, que é chamado decarrier signalpara transmitir nosso sinal de mensagem. Esse processo é chamado simplesmente de modulação.

Modulação é o processo de alterar os parâmetros do sinal da portadora, de acordo com os valores instantâneos do sinal modulante.

Necessidade de modulação

Os sinais de banda base são incompatíveis para transmissão direta. Para tal sinal, para viajar distâncias maiores, sua força tem que ser aumentada modulando com uma onda portadora de alta freqüência, que não afeta os parâmetros do sinal modulante.

Vantagens da modulação

A antena usada para transmissão, tinha que ser muito grande, se a modulação não foi introduzida. O alcance da comunicação fica limitado, pois a onda não pode viajar uma distância sem ser distorcida.

A seguir estão algumas das vantagens de implementar modulação nos sistemas de comunicação.

• Redução do tamanho da antena
• Sem mixagem de sinal
• Maior alcance de comunicação
• Multiplexação de sinais
• Possibilidade de ajustes de largura de banda
• Melhor qualidade de recepção

Sinais no processo de modulação

A seguir estão os três tipos de sinais no processo de modulação.

Mensagem ou sinal modulante

O sinal que contém uma mensagem a ser transmitida é chamado de message signal. É um sinal de banda base, que precisa passar por um processo de modulação para ser transmitido. Por isso, também é chamado demodulating signal.

Carrier Signal

O sinal de alta frequência, que tem uma certa amplitude, frequência e fase, mas não contém informações, é chamado de carrier signal. É um sinal vazio e é usado para transportar o sinal para o receptor após a modulação.

Sinal Modulado

O sinal resultante após o processo de modulação é chamado de modulated signal. Este sinal é uma combinação de sinal de modulação e sinal de portadora.

Tipos de modulação

Existem muitos tipos de modulações. Dependendo das técnicas de modulação utilizadas, elas são classificadas conforme mostrado na figura a seguir.

Os tipos de modulações são amplamente classificados em modulação de onda contínua e modulação de pulso.

Modulação de onda contínua

Na modulação de onda contínua, uma onda senoidal de alta frequência é usada como onda portadora. Isso é dividido em modulação de amplitude e ângulo.

• Se a amplitude da onda portadora de alta frequência for variada de acordo com a amplitude instantânea do sinal modulante, essa técnica é chamada de Amplitude Modulation.

• Se o ângulo da onda portadora for variado, de acordo com o valor instantâneo do sinal modulante, essa técnica é chamada de Angle Modulation. A modulação angular é dividida em modulação de frequência e modulação de fase.

  • Se a frequência da onda portadora for variada, de acordo com o valor instantâneo do sinal modulante, essa técnica é chamada de Frequency Modulation.

  • Se a fase da onda portadora de alta frequência é variada de acordo com o valor instantâneo do sinal modulante, essa técnica é chamada de Phase Modulation.

Modulação de pulso

Na modulação de pulso, uma sequência periódica de pulsos retangulares é usada como onda portadora. Isso é dividido em modulação analógica e digital.

Na técnica de modulação analógica, se a amplitude, duração ou posição de um pulso é variada de acordo com os valores instantâneos do sinal de modulação de banda base, essa técnica é chamada de Modulação de Amplitude de Pulso (PAM) ou Duração de Pulso / Modulação de Largura (PDM / PWM) ou Modulação de posição de pulso (PPM).

Na modulação digital, a técnica de modulação usada é Pulse Code Modulation (PCM), onde o sinal analógico é convertido para a forma digital de 1s e 0s. Como o resultante é um trem de pulso codificado, isso é chamado de PCM. Isso é posteriormente desenvolvido como Delta Modulation (DM). Essas técnicas de modulação digital são discutidas em nosso tutorial de Comunicações Digitais

Uma onda contínua continua continuamente sem quaisquer intervalos e é o sinal de mensagem de banda base, que contém a informação. Esta onda deve ser modulada.

De acordo com a definição padrão, “A amplitude do sinal portador varia de acordo com a amplitude instantânea do sinal modulante”. Ou seja, a amplitude do sinal da portadora não contendo informação varia de acordo com a amplitude do sinal contendo informação, a cada instante. Isso pode ser bem explicado pelas seguintes figuras.

A primeira figura mostra a onda modulante, que é o sinal de mensagem. A próxima é a onda portadora, que é um sinal de alta frequência e não contém informações. Enquanto, o último é a onda modulada resultante.

Pode-se observar que os picos positivo e negativo da onda portadora, estão interligados com uma linha imaginária. Esta linha ajuda a recriar a forma exata do sinal de modulação. Esta linha imaginária na onda portadora é chamada deEnvelope. É igual ao do sinal de mensagem.

Expressões Matemáticas

A seguir estão as expressões matemáticas para essas ondas.

Representação das ondas no domínio do tempo

Deixe o sinal de modulação ser,

$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$

e o sinal da portadora seja,

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Onde,

$ A_m $ e $ A_c $ são a amplitude do sinal de modulação e do sinal da portadora, respectivamente.

$ f_m $ e $ f_c $ são a frequência do sinal modulante e do sinal da portadora, respectivamente.

Então, a equação da onda modulada em amplitude será

$ s (t) = \ left [A_c + A_m \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $ (Equação 1)

Índice de modulação

Uma onda portadora, depois de modulada, se o nível modulado for calculado, essa tentativa é chamada de Modulation Index ou Modulation Depth. Ele afirma o nível de modulação que uma onda portadora sofre.

Reorganize a Equação 1 conforme abaixo.

$ s (t) = A_c \ left [1+ \ left (\ frac {A_m} {A_c} \ right) \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $

$ \ Rightarrow s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $ ( Equação 2)

Onde, $ \ mu $ é o índice de modulação e é igual à razão de $ A_m $ e $ A_c $. Matematicamente, podemos escrever como

$ \ mu = \ frac {A_m} {A_c} $ (Equação 3)

Portanto, podemos calcular o valor do índice de modulação usando a fórmula acima, quando as amplitudes dos sinais de mensagem e portadora são conhecidos.

Agora, vamos derivar mais uma fórmula para o índice de modulação, considerando a Equação 1. Podemos usar esta fórmula para calcular o valor do índice de modulação, quando as amplitudes máxima e mínima da onda modulada são conhecidas.

Sejam $ A_ \ max $ e $ A_ \ min $ as amplitudes máxima e mínima da onda modulada.

Obteremos a amplitude máxima da onda modulada, quando $ \ cos \ left (2 \ pi f_mt \ right) $ é 1.

$ \ Rightarrow A_ \ max = A_c + A_m $ (Equação 4)

Obteremos a amplitude mínima da onda modulada, quando $ \ cos \ left (2 \ pi f_mt \ right) $ é -1.

$ \ Rightarrow A_ \ min = A_c - A_m $ (Equação 5)

Adicione a Equação 4 e a Equação 5.

$$ A_ \ max + A_ \ min = A_c + A_m + A_c-A_m = 2A_c $$

$ \ Rightarrow A_c = \ frac {A_ \ max + A_ \ min} {2} $ (Equação 6)

Subtraia a Equação 5 da Equação 4.

$$ A_ \ max - A_ \ min = A_c + A_m - \ left (A_c -A_m \ right) = 2A_m $$

$ \ Rightarrow A_m = \ frac {A_ \ max - A_ \ min} {2} $ (Equação 7)

A proporção da Equação 7 e da Equação 6 será a seguinte.

$$ \ frac {A_m} {A_c} = \ frac {\ left (A_ {max} - A_ {min} \ right) / 2} {\ left (A_ {max} + A_ {min} \ right) / 2 } $$

$ \ Rightarrow \ mu = \ frac {A_ \ max - A_ \ min} {A_ \ max + A_ \ min} $ (Equação 8)

Portanto, a Equação 3 e a Equação 8 são as duas fórmulas para o índice de modulação. O índice de modulação ou profundidade de modulação é freqüentemente denotado em porcentagem chamada de Porcentagem de Modulação. Vamos pegar opercentage of modulation, apenas multiplicando o valor do índice de modulação por 100.

Para uma modulação perfeita, o valor do índice de modulação deve ser 1, o que implica que o percentual de modulação deve ser 100%.

Por exemplo, se este valor for menor que 1, ou seja, o índice de modulação é 0,5, então a saída modulada seria semelhante à figura a seguir. É chamado deUnder-modulation. Essa onda é chamada deunder-modulated wave.

Se o valor do índice de modulação for maior que 1, ou seja, 1,5 ou mais, então a onda será um over-modulated wave. Seria semelhante à figura a seguir.

À medida que o valor do índice de modulação aumenta, a portadora experimenta uma reversão de fase de 180 ^o , o que causa bandas laterais adicionais e, portanto, a onda fica distorcida. Essa onda supermodulada causa interferência, que não pode ser eliminada.

Largura de banda de AM Wave

Bandwidth(BW) é a diferença entre as frequências mais alta e mais baixa do sinal. Matematicamente, podemos escrever como

$$ BW = f_ {max} - f_ {min} $$

Considere a seguinte equação de onda modulada em amplitude.

$$ s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_c \ mu \ cos (2 \ pi f_ct) \ cos \ left (2 \ pi f_mt \ right) $$

$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $

Portanto, a onda modulada em amplitude tem três frequências. Essas são a frequência da portadora $ f_c $, a frequência da banda lateral superior $ f_c + f_m $ e a frequência da banda lateral inferior $ f_c-f_m $

Aqui,

$ f_ {max} = f_c + f_m $ e $ f_ {min} = f_c-f_m $

Substitua os valores $ f_ {max} $ e $ f_ {min} $ na fórmula de largura de banda.

$$ BW = f_c + f_m- \ left (f_c-f_m \ right) $$

$$ \ Rightarrow BW = 2f_m $$

Assim, pode-se dizer que a largura de banda necessária para a onda modulada em amplitude é o dobro da freqüência do sinal modulante.

Cálculos de potência da onda AM

Considere a seguinte equação de onda modulada em amplitude.

$ \ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ direita) t \ direita] + \ frac {A_c \ mu} {2} \ cos \ esquerda [2 \ pi \ esquerda (f_c-f_m \ direita) t \ direita] $

A potência da onda AM é igual à soma das potências dos componentes de frequência da portadora, banda lateral superior e banda lateral inferior.

$$ P_t = P_c + P_ {USB} + P_ {LSB} $$

Sabemos que a fórmula padrão para a potência do sinal cos é

$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {2} $$

Onde,

$ v_ {rms} $ é o valor rms do sinal cos.

$ v_m $ é o valor de pico do sinal cos.

Primeiro, vamos encontrar os poderes do portador, a banda lateral superior e inferior, uma por uma.

Poder portador

$$ P_c = \ frac {\ left (A_c / \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2}} {2R} $$

Potência da banda lateral superior

$$ P_ {USB} = \ frac {\ left (A_c \ mu / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$

Da mesma forma, obteremos a potência da banda lateral inferior igual à potência da banda lateral superior.

$$ P_ {LSB} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$

Agora, vamos adicionar essas três potências para obter a potência da onda AM.

$$ P_t = \ frac {{A_ {c}} ^ {2}} {2R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$

$$ \ Rightarrow P_t = \ left (\ frac {{A_ {c}} ^ {2}} {2R} \ right) \ left (1+ \ frac {\ mu ^ 2} {4} + \ frac {\ mu ^ 2} {4} \ right) $$

$$ \ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ right) $$

Podemos usar a fórmula acima para calcular a potência da onda AM, quando a potência da portadora e o índice de modulação são conhecidos.

Se o índice de modulação $ \ mu = 1 $, então a potência da onda AM é igual a 1,5 vezes a potência da portadora. Portanto, a potência necessária para transmitir uma onda AM é 1,5 vezes a potência da portadora para uma modulação perfeita.

No capítulo anterior, discutimos os parâmetros usados ​​na modulação em amplitude. Cada parâmetro tem sua própria fórmula. Usando essas fórmulas, podemos encontrar os respectivos valores dos parâmetros. Neste capítulo, vamos resolver alguns problemas com base no conceito de modulação em amplitude.

Problema 1

Um sinal de modulação $ m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right) $ é modulado em amplitude com um sinal de portadora $ c \ left (t \ right) = 50 \ cos \ left (2 \ pi \ vezes 10 ^ 5 t \ right) $. Encontre o índice de modulação, a potência da portadora e a potência necessária para transmitir a onda AM.

Solução

Dado, a equação do sinal de modulação como

$$ m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ vezes 10 ^ 3 t \ right) $$

Conhecemos a equação padrão de modulação de sinal como

$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$

Ao comparar as duas equações acima, obteremos

Amplitude do sinal de modulação como $ A_m = 10 volts $

e Frequência de modulação do sinal como $$ f_m = 10 ^ 3 Hz = 1 KHz $$

Dado, a equação do sinal da portadora é

$$ c \ left (t \ right) = 50 \ cos \ left (2 \ pi \ vezes 10 ^ 5t \ right) $$

A equação padrão do sinal da portadora é

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Ao comparar essas duas equações, obteremos

Amplitude do sinal da portadora como $ A_c = 50volts $

e a frequência do sinal da portadora como $ f_c = 10 ^ 5 Hz = 100 KHz $

Conhecemos a fórmula do índice de modulação como

$$ \ mu = \ frac {A_m} {A_c} $$

Substitua os valores $ A_m $ e $ A_c $ na fórmula acima.

$$ \ mu = \ frac {10} {50} = 0,2 $$

Portanto, o valor de modulation index is 0.2 e a porcentagem de modulação é de 20%.

A fórmula para potência da portadora, $ P_c = $ é

$$ P_c = \ frac {{A_ {c}} ^ {2}} {2R} $$

Assuma $ R = 1 \ Omega $ e substitua o valor $ A_c $ na fórmula acima.

$$ P_c = \ frac {\ left (50 \ right) ^ 2} {2 \ left (1 \ right)} = 1250W $$

Portanto, o Carrier power, $ P_c $ é 1250 watts.

Nós sabemos a fórmula para power requerido para transmitting AM onda é

$$ \ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ right) $$

Substitua os valores $ P_c $ e $ \ mu $ na fórmula acima.

$$ P_t = 1250 \ left (1+ \ frac {\ left (0.2 \ right) ^ 2} {2} \ right) = 1275W $$

Portanto, o power required for transmitting AM onda é 1275 watts.

Problema 2

A equação da onda de amplitude é dada por $ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ right) $. Encontre a potência da portadora, a potência total da banda lateral e a largura de banda da onda AM.

Solução

Dado, a equação da onda modulada em amplitude é

$$ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ right) $$

Reescreva a equação acima como

$$ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (2 \ pi \ times 2 \ times 10 ^ 5t \ right) $$

Sabemos que a equação da onda modulada em amplitude é

$$ s \ left (t \ right) = A_c \ left [1+ \ mu \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

Ao comparar as duas equações acima, obteremos

Amplitude do sinal da portadora como $ A_c = 20 volts $

Índice de modulação como $ \ mu = 0,8 $

Freqüência de modulação do sinal como $ f_m = 10 ^ 3Hz = 1 KHz $

Frequência do sinal da portadora como $ f_c = 2 \ vezes 10 ^ 5Hz = 200KHz $

A fórmula para potência da portadora, $ P_c $ é

$$ P_c = \ frac {{A_ {e}} ^ {2}} {2R} $$

Assuma $ R = 1 \ Omega $ e substitua o valor $ A_c $ na fórmula acima.

$$ P_c = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200W $$

Portanto, o Carrier power, $ P_c $ é 200watts.

Sabemos que a fórmula para a potência total da banda lateral é

$$ P_ {SB} = \ frac {P_c \ mu ^ 2} {2} $$

Substitua os valores $ P_c $ e $ \ mu $ na fórmula acima.

$$ P_ {SB} = \ frac {200 \ times \ left (0.8 \ right) ^ 2} {2} = 64W $$

Portanto, o total side band power é 64 watts.

Sabemos que a fórmula para largura de banda da onda AM é

$$ BW = 2f_m $$

Substitua o valor $ f_m $ na fórmula acima.

$$ BW = 2 \ left (1K \ right) = 2 KHz $$

Portanto, o bandwidth da onda AM é 2 KHz.

Neste capítulo, vamos discutir sobre os moduladores, que geram ondas moduladas em amplitude. Os dois moduladores a seguir geram ondas AM.

• Modulador de lei quadrada
• Modulador de comutação

Modulador Square Law

A seguir está o diagrama de blocos do modulador de lei quadrada

Sejam os sinais de modulação e portadora $ m \ left (t \ right) $ e $ A \ cos \ left (2 \ pi f_ct \ right) $ respectivamente. Esses dois sinais são aplicados como entradas para o bloco de verão (somador). Este bloco de verão produz uma saída, que é a adição do sinal modulante e da portadora. Matematicamente, podemos escrever como

$$ V_1t = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) $$

Este sinal $ V_1t $ é aplicado como uma entrada para um dispositivo não linear como um diodo. As características do diodo estão intimamente relacionadas à lei quadrática.

$ V_2t = k_1V_1 \ left (t \ right) + k_2V_1 ^ 2 \ left (t \ right) $ (Equação 1)

Onde, $ k_1 $ e $ k_2 $ são constantes.

Substitua $ V_1 \ left (t \ right) $ na Equação 1

$$ V_2 \ esquerda (t \ direita) = k_1 \ esquerda [m \ esquerda (t \ direita) + A_c \ cos \ esquerda (2 \ pi f_ct \ direita) \ direita] + k_2 \ esquerda [m \ esquerda (t \ direita) + A_c \ cos \ esquerda (2 \ pi f_ct \ direita) \ direita] ^ 2 $$

$ \ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_1 A_c \ cos \ left (2 \ pi f_ct \ right) + k_2 m ^ 2 \ left (t \ right) + $

$ k_2A_c ^ 2 \ cos ^ 2 \ left (2 \ pi f_ct \ right) + 2k_2m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct \ right) $

$ \ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_2 m ^ 2 \ left (t \ right) + k_2 A ^ 2_c \ cos ^ 2 \ left (2 \ pi f_ct \ direita) + $

$ k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $

O último termo da equação acima representa a onda AM desejada e os três primeiros termos da equação acima são indesejados. Assim, com a ajuda do filtro passa-banda, podemos passar apenas a onda AM e eliminar os três primeiros termos.

Portanto, a saída do modulador de lei quadrada é

$$ s \ left (t \ right) = k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

A equação padrão da onda AM é

$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

Onde, $ K_a $ é a sensibilidade de amplitude

Ao comparar a saída do modulador de lei quadrada com a equação padrão da onda AM, obteremos o fator de escala como $ k_1 $ e a sensibilidade de amplitude $ k_a $ como $ \ frac {2k_2} {k1} $.

Modulador de comutação

A seguir está o diagrama de blocos do modulador de comutação.

O modulador de comutação é semelhante ao modulador de lei quadrada. A única diferença é que no modulador de lei quadrada, o diodo é operado em um modo não linear, ao passo que, no modulador de chaveamento, o diodo deve operar como uma chave ideal.

Deixe os sinais de modulação e portadora serem denotados como $ m \ left (t \ right) $ e $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $ respectivamente. Esses dois sinais são aplicados como entradas para o bloco de verão (somador). O bloco de verão produz uma saída, que é a adição de sinais modulantes e portadores. Matematicamente, podemos escrever como

$$ V_1 \ esquerda (t \ direita) = m \ esquerda (t \ direita) + c \ esquerda (t \ direita) = m \ esquerda (t \ direita) + A_c \ cos \ esquerda (2 \ pi f_ct \ direita ) $$

Este sinal $ V_1 \ left (t \ right) $ é aplicado como uma entrada de diodo. Suponha que a magnitude do sinal de modulação seja muito pequena quando comparada à amplitude do sinal da portadora $ A_c $. Assim, a ação ON e OFF do diodo é controlada pelo sinal da portadora $ c \ left (t \ right) $. Isso significa que o diodo terá polarização direta quando $ c \ left (t \ right)> 0 $ e será polarizado reversamente quando $ c \ left (t \ right) <0 $.

Portanto, a saída do diodo é

$$ V_2 \ left (t \ right) = \ left \ {\ begin {matrix} V_1 \ left (t \ right) & if & c \ left (t \ right)> 0 \\ 0 & if & c \ left (t \ right) <0 \ end {matrix} \ right. $$

Podemos aproximar isso como

$ V_2 \ left (t \ right) = V_1 \ left (t \ right) x \ left (t \ right) $ (Equação 2)

Onde, $ x \ left (t \ right) $ é um trem de pulso periódico com período de tempo $ T = \ frac {1} {f_c} $

A representação da série de Fourier deste trem de pulso periódico é

$$ x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ direita) ^ n-1} {2n-1} \ cos \ left (2 \ pi \ left (2n-1 \ right) f_ct \ right) $$

$$ \ Rightarrow x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} { 3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + .... $$

Substitua os valores $ V_1 \ left (t \ right) $ e $ x \ left (t \ right) $ na Equação 2.

$ V_2 \ left (t \ right) = \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] \ left [\ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + ..... \ right] $

$ V_2 \ left (t \ right) = \ frac {m \ left (t \ right)} {2} + \ frac {A_c} {2} \ cos \ left (2 \ pi f_ct \ right) + \ frac { 2m \ left (t \ right)} {\ pi} \ cos \ left (2 \ pi f_ct \ right) + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ right) - $

$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ direita) \ cos \ esquerda (6 \ pi f_ct \ direita) + ..... $

$ V_2 \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac {m \ left (t \ right)} {2} + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ direita) - $

$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ direita) \ cos \ esquerda (6 \ pi f_ct \ direita) + ..... $

O 1 ^r termo da equação acima representa a onda AM desejado e os restantes termos são termos indesejados. Assim, com a ajuda do filtro passa-banda, podemos passar apenas a onda AM e eliminar os termos restantes.

Portanto, a saída do modulador de comutação é

$$ s \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right ) \ cos \ left (2 \ pi f_ct \ right) $$

Sabemos que a equação padrão da onda AM é

$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

Onde, $ k_a $ é a sensibilidade de amplitude.

Comparando a saída do modulador de comutação com a equação padrão da onda AM, obteremos o fator de escala como 0,5 e a sensibilidade de amplitude $ k_a $ como $ \ frac {4} {\ pi A_c} $.

O processo de extração de um sinal de mensagem original da onda modulada é conhecido como detection ou demodulation. O circuito que demodula a onda modulada é conhecido como odemodulator. Os seguintes demoduladores (detectores) são usados ​​para demodular a onda AM.

• Demodulador de Lei Quadrada
• Detector de Envelope

Demodulador de Lei Quadrada

O demodulador de lei quadrada é usado para demodular a onda AM de baixo nível. A seguir está o diagrama de blocos dosquare law demodulator.

Este demodulador contém um dispositivo de lei quadrada e filtro passa-baixo. A onda AM $ V_1 \ left (t \ right) $ é aplicada como uma entrada para este demodulador.

A forma padrão da onda AM é

$$ V_1 \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

Sabemos que a relação matemática entre a entrada e a saída do dispositivo de lei quadrada é

$ V_2 \ esquerda (t \ direita) = k_1V_1 \ esquerda (t \ direita) + k_2V_1 ^ 2 \ esquerda (t \ direita) $ (Equação 1)

Onde,

$ V_1 \ left (t \ right) $ é a entrada do dispositivo de lei quadrada, que nada mais é do que a onda AM

$ V_2 \ left (t \ right) $ é a saída do dispositivo de lei quadrada

$ k_1 $ e $ k_2 $ são constantes

Substitua $ V_1 \ left (t \ right) $ na Equação 1

$$ V_2 \ esquerda (t \ direita) = k_1 \ esquerda (A_c \ esquerda [1 + k_am \ esquerda (t \ direita) \ direita] \ cos \ esquerda (2 \ pi f_ct \ direita) \ direita) + k_2 \ esquerda (A_c \ esquerda [1 + k_am \ esquerda (t \ direita) \ direita] \ cos \ esquerda (2 \ pi f_ct \ direita) \ direita) ^ 2 $$

$ \ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + $

$ k_2 {A_ {c}} ^ {2} \ esquerda [1+ {K_ {a}} ^ {2} m ^ 2 \ esquerda (t \ direita) + 2k_am \ esquerda (t \ direita) \ direita] \ esquerda (\ frac {1+ \ cos \ esquerda (4 \ pi f_ct \ direita)} {2} \ direita) $

$ \ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac { K_2 {A_ {c}} ^ {2}} {2} + $

$ \ frac {K_2 {A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct \ right) + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a }} ^ {2} m ^ 2 \ left (t \ right)} {2} + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a}} ^ {2} m ^ 2 \ left (t \ direita)} {2} \ cos \ esquerda (4 \ pi f_ct \ direita) + $

$ k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) + k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) \ cos \ left (4 \ pi f_ct \ direita) $

Na equação acima, o termo $ k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) $ é a versão em escala do sinal de mensagem. Ele pode ser extraído passando o sinal acima por um filtro passa-baixo e o componente DC $ \ frac {k_2 {A_ {c}} ^ {2}} {2} $ pode ser eliminado com a ajuda de um capacitor de acoplamento.

Detector de Envelope

O detector de envelope é usado para detectar (demodular) ondas AM de alto nível. A seguir está o diagrama de blocos do detector de envelope.

Este detector de envelope consiste em um diodo e um filtro passa-baixa. Aqui, o diodo é o principal elemento de detecção. Portanto, o detector de envelope também é chamado dediode detector. O filtro passa-baixo contém uma combinação paralela do resistor e do capacitor.

A onda AM $ s \ left (t \ right) $ é aplicada como uma entrada para este detector.

Sabemos que a forma padrão da onda AM é

$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

No meio ciclo positivo da onda AM, o diodo conduz e o capacitor carrega até o valor de pico da onda AM. Quando o valor da onda AM for menor que este valor, o diodo será polarizado reversamente. Assim, o capacitor irá descarregar através do resistorRaté o próximo meio ciclo positivo da onda AM. Quando o valor da onda AM é maior que a tensão do capacitor, o diodo conduz e o processo é repetido.

Devemos selecionar os valores dos componentes de forma que o capacitor carregue muito rapidamente e descarregue muito lentamente. Como resultado, obteremos a forma de onda da tensão do capacitor igual à do envelope da onda AM, que é quase semelhante ao sinal de modulação.

No processo de Modulação em Amplitude, a onda modulada consiste na onda portadora e em duas bandas laterais. A onda modulada possui a informação apenas nas bandas laterais.Sideband nada mais é do que uma banda de frequências, contendo energia, que são as frequências mais baixas e mais altas da frequência portadora.

A transmissão de um sinal, que contém uma portadora junto com duas bandas laterais, pode ser denominada como Double Sideband Full Carrier sistema ou simplesmente DSBFC. Ele é plotado conforme mostrado na figura a seguir.

No entanto, essa transmissão é ineficiente. Porque dois terços da energia estão sendo desperdiçados na transportadora, que não traz nenhuma informação.

Se esta portadora for suprimida e a energia economizada for distribuída para as duas bandas laterais, tal processo é denominado Double Sideband Suppressed Carrier sistema ou simplesmente DSBSC. Ele é plotado conforme mostrado na figura a seguir.

Expressões Matemáticas

Vamos considerar as mesmas expressões matemáticas para sinais de modulação e portadora que consideramos nos capítulos anteriores.

ou seja, sinal de modulação

$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$

Sinal da operadora

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Matematicamente, podemos representar o equation of DSBSC wave como o produto de sinais modulantes e portadores.

$$ s \ left (t \ right) = m \ left (t \ right) c \ left (t \ right) $$

$$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right) $$

Largura de banda do DSBSC Wave

Sabemos que a fórmula para largura de banda (BW) é

$$ BW = f_ {max} -f_ {min} $$

Considere a equação da onda modulada DSBSC.

$$ s \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos (2 \ pi f_ct) $$

$$ \ Rightarrow s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2 } \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$

A onda modulada DSBSC tem apenas duas frequências. Portanto, as frequências máxima e mínima são $ f_c + f_m $ e $ f_c-f_m $ respectivamente.

ie,

$ f_ {max} = f_c + f_m $ e $ f_ {min} = f_c-f_m $

Substitua os valores $ f_ {max} $ e $ f_ {min} $ na fórmula da largura de banda.

$$ BW = f_c + f_m- \ left (f_c-f_m \ right) $$

$$ \ Rightarrow BW = 2f_m $$

Assim, a largura de banda da onda DSBSC é a mesma da onda AM e é igual a duas vezes a freqüência do sinal modulante.

Cálculos de potência de DSBSC Wave

Considere a seguinte equação da onda modulada DSBSC.

$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$

A potência da onda DSBSC é igual à soma das potências da banda lateral superior e dos componentes de frequência da banda lateral inferior.

$$ P_t = P_ {USB} + P_ {LSB} $$

Sabemos que a fórmula padrão para a potência do sinal cos é

$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m \ sqrt {2} \ right) ^ 2} {R} $$

Primeiro, vamos encontrar os poderes da banda lateral superior e inferior, uma a uma.

Potência da banda lateral superior

$$ P_ {USB} = \ frac {\ left (A_mA_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Da mesma forma, obteremos a potência da banda lateral inferior igual à potência da banda lateral superior.

$$ P_ {USB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Agora, vamos adicionar essas duas potências de banda lateral para obter a potência da onda DSBSC.

$$ P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} + \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$

$$ \ Rightarrow P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {4R} $$

Portanto, a potência necessária para transmitir a onda DSBSC é igual à potência de ambas as bandas laterais.

Neste capítulo, vamos discutir sobre os moduladores, que geram ondas DSBSC. Os dois moduladores a seguir geram ondas DSBSC.

• Modulador balanceado
• Modulador de anel

Modulador Balanceado

A seguir está o diagrama de blocos do modulador Balanced.

Balanced modulatorconsiste em dois moduladores AM idênticos. Esses dois moduladores são dispostos em uma configuração balanceada para suprimir o sinal da portadora. Por isso, é chamado de modulador balanceado.

O mesmo sinal de portadora $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $ é aplicado como uma das entradas para esses dois moduladores AM. O sinal de modulação $ m \ left (t \ right) $ é aplicado como outra entrada para o modulador AM superior. Enquanto que o sinal modulante $ m \ left (t \ right) $ com polaridade oposta, ou seja, $ -m \ left (t \ right) $ é aplicado como outra entrada para o modulador AM inferior.

A saída do modulador AM superior é

$$ s_1 \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

A saída do modulador AM inferior é

$$ s_2 \ left (t \ right) = A_c \ left [1-k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

Obtemos a onda DSBSC $ s \ left (t \ right) $ subtraindo $ s_2 \ left (t \ right) $ de $ s_1 \ left (t \ right) $. O bloco de verão é usado para realizar esta operação. $ s_1 \ left (t \ right) $ com sinal positivo e $ s_2 \ left (t \ right) $ com sinal negativo são aplicados como entradas para o bloco de verão. Assim, o bloco de verão produz uma saída $ s \ left (t \ right) $ que é a diferença de $ s_1 \ left (t \ right) $ e $ s_2 \ left (t \ right) $.

$$ \ Rightarrow s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -A_c \ left [1-k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) - A_c \ cos \ left (2 \ pi f_ct \ right) + $$

$ A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $

$ \ Rightarrow s \ left (t \ right) = 2A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $

Sabemos que a equação padrão da onda DSBSC é

$$ s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$

Comparando a saída do bloco de verão com a equação padrão da onda DSBSC, obteremos o fator de escala como $ 2k_a $

Modulador de anel

A seguir está o diagrama de blocos do modulador Ring.

Neste diagrama, os quatro diodos $ D_1 $, $ D_2 $, $ D_3 $ e $ D_4 $ estão conectados na estrutura do anel. Portanto, este modulador é chamado dering modulator. Dois transformadores com derivação central são usados ​​neste diagrama. O sinal de mensagem $ m \ left (t \ right) $ é aplicado ao transformador de entrada. Enquanto que os sinais da portadora $ c \ left (t \ right) $ são aplicados entre os dois transformadores com derivação central.

Para meio ciclo positivo do sinal da portadora, os diodos $ D_1 $ e $ D_3 $ são LIGADOS e os outros dois diodos $ D_2 $ e $ D_4 $ são DESLIGADOS. Neste caso, o sinal de mensagem é multiplicado por +1.

Para meio ciclo negativo do sinal da portadora, os diodos $ D_2 $ e $ D_4 $ são LIGADOS e os outros dois diodos $ D_1 $ e $ D_3 $ são DESLIGADOS. Neste caso, o sinal de mensagem é multiplicado por -1. Isso resulta em $ 180 ^ 0 $ mudança de fase na onda DSBSC resultante.

A partir da análise acima, podemos dizer que os quatro diodos $ D_1 $, $ D_2 $, $ D_3 $ e $ D_4 $ são controlados pelo sinal da portadora. Se a portadora for uma onda quadrada, a representação da série de Fourier de $ c \ left (t \ right) $ é representada como

$$ c \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ right] $$

Obteremos DSBSC wave $ s \ left (t \ right) $, que é apenas o produto do sinal da portadora $ c \ left (t \ right) $ e o sinal de mensagem $ m \ left (t \ right) $ ie ,

$$ s \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ right] m \ left (t \ right) $$

A equação acima representa a onda DSBSC, que é obtida no transformador de saída do modulador em anel.

Moduladores DSBSC também são chamados de product modulators à medida que produzem a saída, que é o produto de dois sinais de entrada.

O processo de extração de um sinal de mensagem original da onda DSBSC é conhecido como detecção ou demodulação de DSBSC. Os seguintes demoduladores (detectores) são usados ​​para demodular a onda DSBSC.

• Detector Coerente
• Costas Loop

Detector Coerente

Aqui, o mesmo sinal de portadora (que é usado para gerar sinal DSBSC) é usado para detectar o sinal de mensagem. Portanto, este processo de detecção é chamado decoherent ou synchronous detection. A seguir está o diagrama de blocos do detector coerente.

Neste processo, o sinal de mensagem pode ser extraído da onda DSBSC multiplicando-o por uma portadora, tendo a mesma frequência e fase da portadora utilizada na modulação DSBSC. O sinal resultante é então passado por um filtro passa-baixas. A saída deste filtro é o sinal de mensagem desejado.

Deixe a onda DSBSC ser

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$

A saída do oscilador local é

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi \ right) $$

Onde, $ \ phi $ é a diferença de fase entre o sinal do oscilador local e o sinal da portadora, que é usado para modulação DSBSC.

A partir da figura, podemos escrever a saída do modulador de produto como

$$ v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right) $$

Substitua os valores $ s \ left (t \ right) $ e $ c \ left (t \ right) $ na equação acima.

$$ \ Rightarrow v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct + \ phi \ right) $$

$ = {A_ {c}} ^ {2} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) m \ left (t \ right) $

$ = \ frac {{A_ {c}} ^ {2}} {2} \ left [\ cos \ left (4 \ pi f_ct + \ phi \ right) + \ cos \ phi \ right] m \ left (t \ direita) $

$$ v \ left (t \ right) = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right) + \ frac {{A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right) $$

Na equação acima, o primeiro termo é a versão em escala do sinal de mensagem. Ele pode ser extraído passando o sinal acima por um filtro passa-baixo.

Portanto, a saída do filtro passa-baixa é

$$ v_0t = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right) $$

A amplitude do sinal demodulado será máxima, quando $ \ phi = 0 ^ 0 $. É por isso que o sinal do oscilador local e o sinal da portadora devem estar em fase, ou seja, não deve haver nenhuma diferença de fase entre esses dois sinais.

A amplitude do sinal demodulado será zero, quando $ \ phi = \ pm 90 ^ 0 $. Este efeito é chamado dequadrature null effect.

Costas Loop

O loop de Costas é usado para fazer o sinal da portadora (usado para modulação DSBSC) e o sinal gerado localmente em fase. A seguir está o diagrama de blocos do loop de Costas.

Costas loopconsiste em dois moduladores de produto com entrada comum $ s \ left (t \ right) $, que é onda DSBSC. A outra entrada para ambos os moduladores de produto é retirada deVoltage Controlled Oscillator (VCO) com mudança de fase $ -90 ^ 0 $ para um dos moduladores do produto, conforme mostrado na figura.

Sabemos que a equação da onda DSBSC é

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$

Deixe a saída do VCO ser

$$ c_1 \ left (t \ right) = \ cos \ left (2 \ pi f_ct + \ phi \ right) $$

Esta saída de VCO é aplicada como a entrada da portadora do modulador de produto superior.

Portanto, a saída do modulador de produto superior é

$$ v_1 \ left (t \ right) = s \ left (t \ right) c_1 \ left (t \ right) $$

Substitua os valores $ s \ left (t \ right) $ e $ c_1 \ left (t \ right) $ na equação acima.

$$ \ Rightarrow v_1 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) $ $

Após simplificar, obteremos $ v_1 \ left (t \ right) $ as

$$ v_1 \ left (t \ right) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right) + \ frac {A_c} {2} \ cos \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right) $$

Este sinal é aplicado como uma entrada do filtro passa-baixo superior. A saída deste filtro passa-baixa é

$$ v_ {01} \ left (t \ right) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right) $$

Portanto, a saída desse filtro passa-baixa é a versão em escala do sinal de modulação.

A saída do deslocador de fase $ -90 ^ 0 $ é

$$ c_2 \ left (t \ right) = cos \ left (2 \ pi f_ct + \ phi-90 ^ 0 \ right) = \ sin \ left (2 \ pi f_ct + \ phi \ right) $$

Este sinal é aplicado como a entrada da portadora do modulador de produto inferior.

A saída do modulador de produto inferior é

$$ v_2 \ left (t \ right) = s \ left (t \ right) c_2 \ left (t \ right) $$

Substitua os valores $ s \ left (t \ right) $ e $ c_2 \ left (t \ right) $ na equação acima.

$$ \ Rightarrow v_2 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ sin \ left (2 \ pi f_ct + \ phi \ right) $ $

Depois de simplificar, obteremos $ v_2 \ left (t \ right) $ as

$$ v_2 \ left (t \ right) = \ frac {A_c} {2} \ sin \ phi m \ left (t \ right) + \ frac {A_c} {2} \ sin \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right) $$

Este sinal é aplicado como uma entrada do filtro passa-baixo inferior. A saída deste filtro passa-baixa é

$$ v_ {02} \ left (t \ right) = \ frac {A_c} {2} \ sin \ phi m \ left (t \ right) $$

A saída desse filtro passa-baixo tem $ -90 ^ 0 $ de diferença de fase com a saída do filtro passa-baixo superior.

As saídas desses dois filtros passa-baixas são aplicadas como entradas do discriminador de fase. Com base na diferença de fase entre esses dois sinais, o discriminador de fase produz um sinal de controle DC.

Este sinal é aplicado como uma entrada do VCO para corrigir o erro de fase na saída do VCO. Portanto, o sinal da portadora (usado para modulação DSBSC) e o sinal gerado localmente (saída VCO) estão em fase.

Nos capítulos anteriores, discutimos a modulação e demodulação DSBSC. O sinal modulado DSBSC possui duas bandas laterais. Como as duas bandas laterais carregam as mesmas informações, não há necessidade de transmitir as duas bandas laterais. Podemos eliminar uma banda lateral.

O processo de suprimir uma das bandas laterais junto com a portadora e transmitir uma única banda lateral é chamado de Single Sideband Suppressed Carrier sistema ou simplesmente SSBSC. Ele é plotado conforme mostrado na figura a seguir.

Na figura acima, o portador e a faixa lateral inferior são suprimidos. Portanto, a banda lateral superior é usada para transmissão. Da mesma forma, podemos suprimir a portadora e a banda lateral superior enquanto transmitimos a banda lateral inferior.

Este sistema SSBSC, que transmite uma única banda lateral, tem alta potência, já que a potência alocada para a portadora e a outra banda lateral é utilizada na transmissão desta banda lateral única.

Expressões Matemáticas

Vamos considerar as mesmas expressões matemáticas para os sinais de modulação e portadora que consideramos nos capítulos anteriores.

ou seja, sinal de modulação

$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$

Sinal da operadora

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Matematicamente, podemos representar a equação da onda SSBSC como

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ para a banda lateral superior

Ou

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $ para a banda lateral inferior

Largura de banda do SSBSC Wave

Sabemos que a onda modulada DSBSC contém duas bandas laterais e sua largura de banda é $ 2f_m $. Uma vez que a onda modulada SSBSC contém apenas uma banda lateral, sua largura de banda é a metade da largura de banda da onda modulada DSBSC.

ie, Bandwidth of SSBSC modulated wave = $ \ frac {2f_m} {2} = f_m $

Portanto, a largura de banda da onda modulada SSBSC é $ f_m $ e é igual à frequência do sinal modulante.

Cálculos de potência do SSBSC Wave

Considere a seguinte equação da onda modulada SSBSC.

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ para a banda lateral superior

Ou

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $ para a banda lateral inferior

A potência da onda SSBSC é igual à potência de qualquer um dos componentes de frequência da banda lateral.

$$ P_t = P_ {USB} = P_ {LSB} $$

Sabemos que a fórmula padrão para a potência do sinal cos é

$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {R} $$

Neste caso, o poder da banda lateral superior é

$$ P_ {USB} = \ frac {\ left (A_m A_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$

Da mesma forma, obteremos a potência da banda lateral inferior igual à potência da banda lateral superior.

$$ P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Portanto, o poder da onda SSBSC é

$$ P_t = P_ {USB} = P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Vantagens

• A largura de banda ou o espaço de espectro ocupado é menor do que as ondas AM e DSBSC.

• A transmissão de mais número de sinais é permitida.

• O poder é salvo.

• Sinal de alta potência pode ser transmitido.

• Menos ruído está presente.

• O desvanecimento do sinal é menos provável de ocorrer.

Desvantagens

• A geração e detecção da onda SSBSC é um processo complexo.

• A qualidade do sinal é afetada, a menos que o transmissor e receptor SSB tenham uma excelente estabilidade de frequência.

Formulários

• Para requisitos de economia de energia e requisitos de baixa largura de banda.

• Em comunicações móveis terrestres, aéreas e marítimas.

• Em comunicações ponto a ponto.

• Em comunicações de rádio.

• Em televisão, telemetria e comunicações de radar.

• Em comunicações militares, como rádio amador, etc.

Neste capítulo, vamos discutir sobre os moduladores, que geram a onda SSBSC. Podemos gerar a onda SSBSC usando os dois métodos a seguir.

• Método de discriminação de frequência
• Método de discriminação de fase

Método de Discriminação de Frequência

A figura a seguir mostra o diagrama de blocos do modulador SSBSC usando o método de discriminação de frequência.

Neste método, primeiro iremos gerar a onda DSBSC com a ajuda do modulador do produto. Em seguida, aplique esta onda DSBSC como uma entrada do filtro passa-banda. Este filtro passa-banda produz uma saída, que é onda SSBSC.

Selecione a faixa de frequência do filtro passa-banda como o espectro da onda SSBSC desejada. Isso significa que o filtro passa-banda pode ser sintonizado nas frequências da banda lateral superior ou inferior para obter a respectiva onda SSBSC com banda lateral superior ou banda lateral inferior.

Método de Discriminação de Fase

A figura a seguir mostra o diagrama de blocos do modulador SSBSC usando o método de discriminação de fase.

Este diagrama de blocos consiste em dois moduladores de produto, dois deslocadores de fase $ -90 ^ 0 $, um oscilador local e um bloco de verão. O modulador de produto produz uma saída, que é o produto de duas entradas. O deslocador de fase $ -90 ^ 0 $ produz uma saída, que tem uma defasagem de fase de $ -90 ^ 0 $ em relação à entrada.

O oscilador local é usado para gerar o sinal da portadora. O bloco de verão produz uma saída, que é a soma de duas entradas ou a diferença de duas entradas com base na polaridade das entradas.

O sinal modulante $ A_m \ cos \ left (2 \ pi f_mt \ right) $ e o sinal da portadora $ A_c \ cos \ left (2 \ pi f_ct \ right) $ são aplicados diretamente como entradas para o modulador de produto superior. Portanto, o modulador de produto superior produz uma saída, que é o produto dessas duas entradas.

A saída do modulador de produto superior é

$$ s_1 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right) $$

$$ \ Rightarrow s_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ esquerda [2 \ pi \ esquerda (f_c-f_m \ direita) t \ direita] \ direita \} $$

O sinal modulante $ A_m \ cos \ left (2 \ pi f_mt \ right) $ e o sinal da portadora $ A_c \ cos \ left (2 \ pi f_ct \ right) $ são deslocados de fase por $ -90 ^ 0 $ antes de aplicar como entradas para o modulador de produto inferior. Portanto, o modulador de produto inferior produz uma saída, que é o produto dessas duas entradas.

A saída do modulador de produto inferior é

$$ s_2 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt-90 ^ 0 \ right) \ cos \ left (2 \ pi f_ct-90 ^ 0 \ right) $$

$ \ Rightarrow s_2 \ left (t \ right) = A_mA_c \ sin \ left (2 \ pi f_mt \ right) \ sin \ left (2 \ pi f_ct \ right) $

$ \ Rightarrow s_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ right \} $

Adicione $ s_1 \ left (t \ right) $ e $ s_2 \ left (t \ right) $ para obter a onda modulada SSBSC $ s \ left (t \ right) $ tendo uma banda lateral inferior.

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} + $

$ \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \ direita) t \ right] \ right \} $

$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $

Subtraia $ s_2 \ left (t \ right) $ de $ s_1 \ left (t \ right) $ para obter a onda modulada SSBSC $ s \ left (t \ right) $ com uma banda lateral superior.

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} - $

$ \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \ direita) t \ right] \ right \} $

$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $

Portanto, ao escolher corretamente as polaridades das entradas no bloco de verão, obteremos a onda SSBSC com uma banda lateral superior ou inferior.

O processo de extração de um sinal de mensagem original da onda SSBSC é conhecido como detecção ou demodulação de SSBSC. O detector coerente é usado para demodulação da onda SSBSC.

Detector Coerente

Aqui, o mesmo sinal de portadora (que é usado para gerar onda SSBSC) é usado para detectar o sinal de mensagem. Portanto, este processo de detecção é chamado decoherent ou synchronous detection. A seguir está o diagrama de blocos do detector coerente.

Neste processo, o sinal de mensagem pode ser extraído da onda SSBSC multiplicando-o por uma portadora, tendo a mesma frequência e fase da portadora utilizada na modulação SSBSC. O sinal resultante é então passado por um filtro passa-baixas. A saída desse filtro é o sinal de mensagem desejado.

Considere o seguinte SSBSC onda tendo um lower sideband.

$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$

A saída do oscilador local é

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

A partir da figura, podemos escrever a saída do modulador de produto como

$$ v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right) $$

Substitua os valores $ s \ left (t \ right) $ e $ c \ left (t \ right) $ na equação acima.

$$ v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ right) $$

$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c -f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ right) $

$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-fm \ right) \ right] + \ cos \ left ( 2 \ pi f_m \ right) t \ right \} $

$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] $

Na equação acima, o primeiro termo é a versão em escala do sinal de mensagem. Ele pode ser extraído passando o sinal acima por um filtro passa-baixo.

Portanto, a saída do filtro passa-baixa é

$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$

Aqui, o fator de escala é $ \ frac {{A_ {c}} ^ {2}} {4} $.

Podemos usar o mesmo diagrama de blocos para demodular a onda SSBSC com uma banda lateral superior. Considere o seguinteSSBSC onda tendo um upper sideband.

$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $$

A saída do oscilador local é

$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$

Podemos escrever a saída do modulador do produto como

$$ v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right) $$

Substitua os valores $ s \ left (t \ right) $ e $ c \ left (t \ right) $ na equação acima.

$$ \ Rightarrow v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ right) $$

$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ right) $

$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} $

$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] $

Na equação acima, o primeiro termo é a versão em escala do sinal de mensagem. Ele pode ser extraído passando o sinal acima por um filtro passa-baixo.

Portanto, a saída do filtro passa-baixa é

$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$

Aqui também o fator de escala é $ \ frac {{A_ {c}} ^ {2}} {4} $.

Portanto, obtemos a mesma saída demodulada em ambos os casos usando um detector coerente.

Nos capítulos anteriores, discutimos a modulação e a demodulação SSBSC. O sinal modulado SSBSC tem apenas uma frequência de banda lateral. Teoricamente, podemos obter um componente de frequência de banda lateral completamente usando um filtro passa-banda ideal. No entanto, praticamente não podemos obter todo o componente de frequência da banda lateral. Devido a isso, algumas informações se perdem.

Para evitar essa perda, uma técnica é escolhida, que é um meio-termo entre DSBSC e SSBSC. Esta técnica é conhecida comoVestigial Side Band Suppressed Carrier (VSBSC)técnica. A palavra “vestígio” significa “uma parte” da qual o nome é derivado.

VSBSC Modulationé o processo em que uma parte do sinal denominado vestígio é modulada junto com uma faixa lateral. O espectro de frequência da onda VSBSC é mostrado na figura a seguir.

Junto com a banda lateral superior, uma parte da banda lateral inferior também está sendo transmitida nesta técnica. Da mesma forma, podemos transmitir a banda lateral inferior junto com uma parte da banda lateral superior. Uma faixa de proteção de largura muito pequena é colocada em cada lado do VSB para evitar as interferências. A modulação VSB é usada principalmente em transmissões de televisão.

Largura de banda da modulação VSBSC

Sabemos que a largura de banda da onda modulada SSBSC é $ f_m $. Visto que a onda modulada VSBSC contém os componentes de frequência de uma banda lateral junto com o vestígio da outra banda lateral, a largura de banda dela será a soma da largura de banda da onda modulada SSBSC e a frequência vestígio $ f_v $.

i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$

Vantagens

A seguir estão as vantagens da modulação VSBSC.

• Altamente eficiente.

• Redução da largura de banda quando comparada às ondas AM e DSBSC.

• O projeto do filtro é fácil, pois não é necessária alta precisão.

• A transmissão de componentes de baixa frequência é possível, sem qualquer dificuldade.

• Possui boas características de fase.

Desvantagens

A seguir estão as desvantagens da modulação VSBSC.

• A largura de banda é maior quando comparada à onda SSBSC.

• A demodulação é complexa.

Formulários

A aplicação mais proeminente e padrão do VSBSC é a transmissão de sinais de televisão. Além disso, essa é a técnica mais conveniente e eficiente quando o uso da largura de banda é considerado.

Agora, vamos discutir sobre o modulador que gera a onda VSBSC e o demodulador que demodula a onda VSBSC uma por uma.

Geração de VSBSC

A geração da onda VSBSC é semelhante à geração da onda SSBSC. O modulador VSBSC é mostrado na figura a seguir.

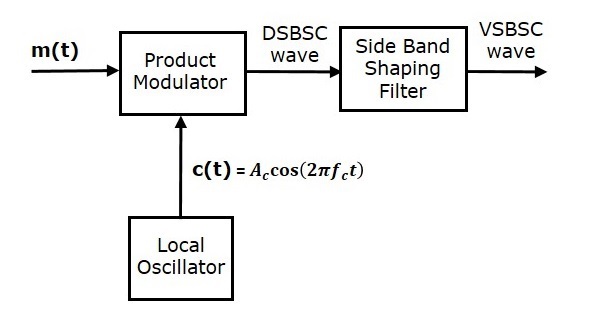
Neste método, primeiro iremos gerar a onda DSBSC com a ajuda do modulador do produto. Em seguida, aplique esta onda DSBSC como uma entrada do filtro de modelagem de banda lateral. Este filtro produz uma saída, que é onda VSBSC.

O sinal de modulação $ m \ left (t \ right) $ e o sinal da portadora $ A_c \ cos \ left (2 \ pi f_ct \ right) $ são aplicados como entradas para o modulador de produto. Assim, o modulador de produto produz uma saída, que é o produto dessas duas entradas.

Portanto, a saída do modulador do produto é

$$ p \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$

Aplicar transformada de Fourier em ambos os lados

$$ P \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] $$

A equação acima representa a equação do espectro de frequência DSBSC.

Seja a função de transferência do filtro de modelagem da banda lateral $ H \ left (f \ right) $. Este filtro tem a entrada $ p \ left (t \ right) $ e a saída é a onda modulada VSBSC $ s \ left (t \ right) $. As transformadas de Fourier de $ p \ left (t \ right) $ e $ s \ left (t \ right) $ são $ P \ left (t \ right) $ e $ S \ left (t \ right) $ respectivamente.

Matematicamente, podemos escrever $ S \ left (f \ right) $ como

$$ S \ left (t \ right) = P \ left (f \ right) H \ left (f \ right) $$

Substitua o valor $ P \ left (f \ right) $ na equação acima.

$$ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ left ( f \ right) $$

A equação acima representa a equação do espectro de frequência VSBSC.

Demodulação de VSBSC

A demodulação da onda VSBSC é semelhante à demodulação da onda SSBSC. Aqui, o mesmo sinal de portadora (que é usado para gerar a onda VSBSC) é usado para detectar o sinal de mensagem. Portanto, este processo de detecção é chamado decoherent ou synchronous detection. O demodulador VSBSC é mostrado na figura a seguir.

Neste processo, o sinal de mensagem pode ser extraído da onda VSBSC multiplicando-o por uma portadora, que está tendo a mesma frequência e fase da portadora utilizada na modulação VSBSC. O sinal resultante é então passado por um filtro passa-baixas. A saída desse filtro é o sinal de mensagem desejado.

Seja a onda VSBSC $ s \ left (t \ right) $ e o sinal da portadora é $ A_c \ cos \ left (2 \ pi f_ct \ right) $.

A partir da figura, podemos escrever a saída do modulador de produto como

$$ v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) s \ left (t \ right) $$

Aplicar transformada de Fourier em ambos os lados

$$ V \ left (f \ right) = \ frac {A_c} {2} \ left [S \ left (f-f_c \ right) + S \ left (f + f_c \ right) \ right] $$

Sabemos que $ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ esquerda (f \ direita) $

A partir da equação acima, vamos encontrar $ S \ left (f-f_c \ right) $ e $ S \ left (f + f_c \ right) $.

$$ S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c-f_c \ right) + M \ left (f-f_c + f_c \ right) \ direita] H \ esquerda (f-f_c \ direita) $$

$ \ Rightarrow S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-2f_c \ right) + M \ left (f \ right) \ right] H \ left (f-f_c \ right) $

$$ S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f + f_c-f_c \ right) + M \ left (f + f_c + f_c \ right) \ direita] H \ esquerda (f + f_c \ direita) $$

$ \ Rightarrow S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f \ right) + M \ left (f + 2f_c \ right) \ right] H \ left (f + f_c \ right) $

Substitua, $ S \ left (f-f_c \ right) $ e $ S \ left (f + f_c \ right) $ valores em $ V \ left (f \ right) $.

$ V (f) = \ frac {A_c} {2} [\ frac {A_c} {2} [M (f-2f_c) + M (f)] H (f-f_c) + $

$ \ frac {A_c} {2} [M (f) + M (f + 2f_c)] H (f + f_c)] $

$ \ Rightarrow V \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ esquerda (f + f_c \ direita) \ direita] $

$ + \ frac {{A_ {c}} ^ {2}} {4} \ left [M \ left (f-2f_c \ right) H \ left (f-f_c \ right) + M \ left (f + 2f_c \ direita) H \ esquerda (f + f_c \ direita) \ direita] $

Na equação acima, o primeiro termo representa a versão em escala do espectro de frequência do sinal de mensagem desejado. Ele pode ser extraído passando o sinal acima por um filtro passa-baixo.

$$ V_0 \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ left (f + f_c \ right) \ right] $$

O outro tipo de modulação na modulação de onda contínua é Angle Modulation. Modulação angular é o processo no qual a frequência ou a fase do sinal da portadora varia de acordo com o sinal de mensagem.

A equação padrão da onda modulada em ângulo é

$$ s \ left (t \ right) = A_c \ cos \ theta _i \ left (t \ right) $$

Onde,

$ A_c $ é a amplitude da onda modulada, que é igual à amplitude do sinal da portadora

$ \ theta _i \ left (t \ right) $ é o ângulo da onda modulada

A modulação angular é dividida em modulação de frequência e modulação de fase.

• Frequency Modulation é o processo de variação da frequência do sinal da portadora linearmente com o sinal de mensagem.

• Phase Modulation é o processo de variar a fase do sinal da portadora linearmente com o sinal de mensagem.

Agora, vamos discutir isso em detalhes.

Modulação de frequência

Na modulação de amplitude, a amplitude do sinal da portadora varia. Considerando que, emFrequency Modulation (FM), a frequência do sinal portador varia de acordo com a amplitude instantânea do sinal modulante.

Portanto, na modulação de frequência, a amplitude e a fase do sinal da portadora permanecem constantes. Isso pode ser melhor compreendido observando as seguintes figuras.

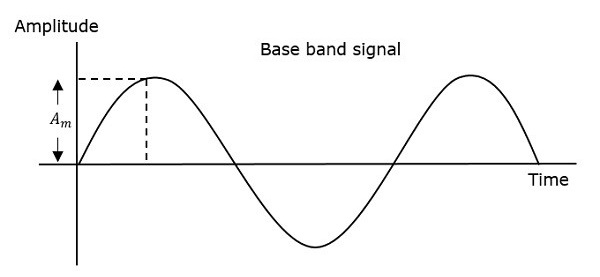
A frequência da onda modulada aumenta, quando a amplitude do sinal modulante ou de mensagem aumenta. Da mesma forma, a frequência da onda modulada diminui, quando a amplitude do sinal modulante diminui. Observe que, a frequência da onda modulada permanece constante e é igual à frequência do sinal da portadora, quando a amplitude do sinal modulante é zero.

Representação Matemática

A equação para frequência instantânea $ f_i $ na modulação FM é

$$ f_i = f_c + k_fm \ left (t \ right) $$

Onde,

$ f_c $ é a frequência portadora

$ k_t $ é a sensibilidade à frequência

$ m \ left (t \ right) $ é o sinal de mensagem

Conhecemos a relação entre a frequência angular $ \ omega_i $ e o ângulo $ \ theta _i \ left (t \ right) $ como

$$ \ omega_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $$

$ \ Rightarrow 2 \ pi f_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $

$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi \ int f_i dt $

Substitua o valor $ f_i $ na equação acima.

$$ \ theta _i \ left (t \ right) = 2 \ pi \ int \ left (f_c + k_f m \ left (t \ right) \ right) dt $$

$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt $

Substitua, $ \ theta _i \ left (t \ right) $ valor na equação padrão da onda modulada em ângulo.

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$

Isto é o equation of FM wave.

Se o sinal de modulação é $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $, então a equação da onda FM será

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right) $$

Onde,

$ \ beta $ = modulation index $ = \ frac {\ Delta f} {f_m} = \ frac {k_fA_m} {f_m} $

A diferença entre a frequência modulada FM (frequência instantânea) e a frequência portadora normal é denominada Frequency Deviation. É denotado por $ \ Delta f $, que é igual ao produto de $ k_f $ e $ A_m $.

FM pode ser dividido em Narrowband FM e Wideband FM com base nos valores do índice de modulação $ \ beta $.

Narrowband FM

A seguir estão os recursos do Narrowband FM.

• Esta modulação de frequência tem uma largura de banda pequena quando comparada ao FM de banda larga.

• O índice de modulação $ \ beta $ é pequeno, ou seja, menor que 1.

• Seu espectro consiste na portadora, a banda lateral superior e a banda lateral inferior.

• Isso é usado em comunicações móveis, como sem fio da polícia, ambulâncias, táxis, etc.

Wideband FM

A seguir estão os recursos do Wideband FM.

• Esta modulação de frequência tem largura de banda infinita.

• O índice de modulação $ \ beta $ é grande, ou seja, superior a 1.

• Seu espectro consiste em uma portadora e um número infinito de bandas laterais, que estão localizadas ao seu redor.

• Isso é usado em entretenimento, aplicativos de transmissão, como rádio FM, TV, etc.

Modulação de Fase

Na modulação de frequência, a frequência da portadora varia. Considerando que, emPhase Modulation (PM), a fase do sinal portador varia de acordo com a amplitude instantânea do sinal modulante.

Portanto, na modulação de fase, a amplitude e a frequência do sinal da portadora permanecem constantes. Isso pode ser melhor compreendido observando as seguintes figuras.

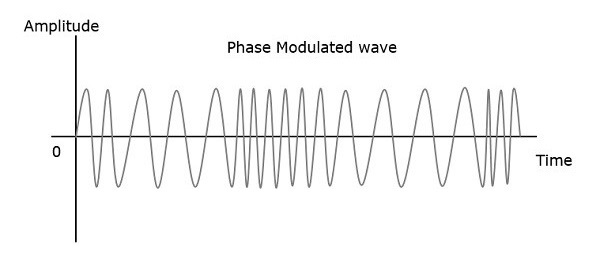
A fase da onda modulada possui infinitos pontos, onde pode ocorrer a mudança de fase em uma onda. A amplitude instantânea do sinal modulante muda a fase do sinal da portadora. Quando a amplitude é positiva, a fase muda em uma direção e se a amplitude for negativa, a fase muda na direção oposta.

Representação Matemática

A equação para a fase instantânea $ \ phi_i $ na modulação de fase é

$$ \ phi _i = k_p m \ left (t \ right) $$

Onde,

• $ k_p $ é a sensibilidade da fase

• $ m \ left (t \ right) $ é o sinal de mensagem

A equação padrão da onda modulada em ângulo é

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi_i \ right) $$

Substitua o valor $ \ phi_i $ na equação acima.

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + k_p m \ left (t \ right) \ right) $$

Isto é o equation of PM wave.

Se o sinal de modulação, $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $, então a equação da onda PM será

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ cos \ left (2 \ pi f_mt \ right) \ right) $$

Onde,

• $ \ beta $ = modulation index = $ \ Delta \ phi = k_pA_m $

• $ \ Delta \ phi $ é o desvio de fase

A modulação de fase é usada em sistemas de comunicação móvel, enquanto a modulação de frequência é usada principalmente para transmissão FM.

No capítulo anterior, discutimos os parâmetros usados ​​na modulação de ângulo. Cada parâmetro tem sua própria fórmula. Usando essas fórmulas, podemos encontrar os respectivos valores dos parâmetros. Neste capítulo, vamos resolver alguns problemas com base no conceito de modulação em frequência.

Problema 1

Uma forma de onda modulante sinusoidal de amplitude 5 V e uma frequência de 2 KHz é aplicada ao gerador de FM, que tem uma sensibilidade de frequência de 40 Hz / volt. Calcule o desvio de frequência, índice de modulação e largura de banda.

Solução

Dada a amplitude do sinal de modulação, $ A_m = 5V $

Frequência de modulação do sinal, $ f_m = 2 KHz $

Sensibilidade de frequência, $ k_f = 40 Hz / volt $

Conhecemos a fórmula para desvio de frequência como

$$ \ Delta f = k_f A_m $$

Substitua os valores $ k_f $ e $ A_m $ na fórmula acima.

$$ \ Delta f = 40 \ vezes 5 = 200Hz $$

Portanto, frequency deviation, $ \ Delta f $ é $ 200Hz $

A fórmula para o índice de modulação é

$$ \ beta = \ frac {\ Delta f} {f_m} $$

Substitua os valores $ \ Delta f $ e $ f_m $ na fórmula acima.

$$ \ beta = \ frac {200} {2 \ vezes 1000} = 0,1 $$

Aqui, o valor de modulation index, $ \ beta $ é 0,1, que é menos de um. Portanto, é Narrow Band FM.

A fórmula para a largura de banda da banda estreita FM é a mesma da onda AM.

$$ BW = 2f_m $$

Substitua o valor $ f_m $ na fórmula acima.

$$ BW = 2 \ vezes 2K = 4KHz $$

Portanto, o bandwidth da onda FM de banda estreita é $ 4 KHz $.

Problema 2

Uma onda FM é dada por $ s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ right ) $. Calcule o desvio de frequência, largura de banda e potência da onda FM.

Solução

Dado, a equação de uma onda FM como

$$ s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ right) $$

Conhecemos a equação padrão de uma onda FM como

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right) $$

Obteremos os seguintes valores comparando as duas equações acima.

Amplitude do sinal da portadora, $ A_c = 20V $

Frequência do sinal da portadora, $ f_c = 4 \ vezes 10 ^ 6 Hz = 4 MHz $

Frequência do sinal de mensagem, $ f_m = 1 \ vezes 10 ^ 3 Hz = 1KHz $

Índice de modulação, $ \ beta = 9 $

Aqui, o valor do índice de modulação é maior que um. Portanto, éWide Band FM.

Conhecemos a fórmula do índice de modulação como

$$ \ beta = \ frac {\ Delta f} {f_m} $$

Reorganize a equação acima como segue.

$$ \ Delta = \ beta f_m $$

Substitua os valores $ \ beta $ e $ f_m $ na equação acima.

$$ \ Delta = 9 \ vezes 1K = 9 KHz $$

Portanto, frequency deviation, $ \ Delta f $ é $ 9 KHz $.

A fórmula para largura de banda da onda FM de banda larga é

$$ BW = 2 \ left (\ beta +1 \ right) f_m $$

Substitua os valores $ \ beta $ e $ f_m $ na fórmula acima.

$$ BW = 2 \ left (9 +1 \ right) 1K = 20KHz $$

Portanto, o bandwidth da onda FM de banda larga é $ 20 KHz $

A fórmula para a potência da onda FM é

$$ P_c = \ frac {{A_ {c}} ^ {2}} {2R} $$

Suponha, $ R = 1 \ Omega $ e substitua o valor $ A_c $ na equação acima.

$$ P = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200W $$

Portanto, o power da onda FM é $ 200 $ watts.

Neste capítulo, vamos discutir sobre os moduladores que geram ondas NBFM e WBFM. Primeiro, vamos discutir sobre a geração de NBFM.

Geração de NBFM

Sabemos que a equação padrão da onda FM é

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$

$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) - $

$ A_c \ sin \ left (2 \ pi f_ct \ right) \ sin \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) $

Para NBFM,

$$ \ left | 2 \ pi k_f \ int m \ left (t \ right) dt \ right | <<1 $$

Sabemos que $ \ cos \ theta \ approx 1 $ e $ \ sin \ theta \ approx 1 $ quando $ \ theta $ é muito pequeno.

Usando as relações acima, obteremos o NBFM equation Como

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) -A_c \ sin \ left (2 \ pi f_ct \ right) 2 \ pi k_f \ int m \ left (t \ direita) dt $$

O diagrama de blocos do modulador NBFM é mostrado na figura a seguir.

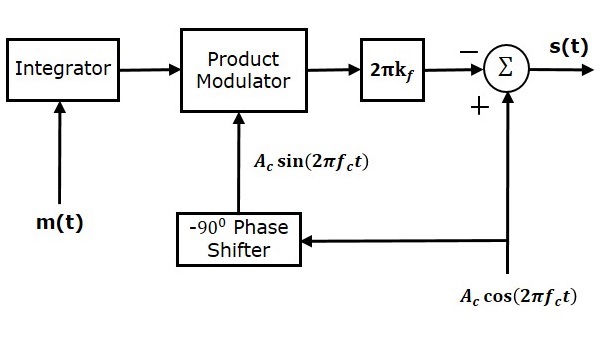
Aqui, o integrador é usado para integrar o sinal de modulação $ m \ left (t \ right) $. O sinal da portadora $ A_c \ cos \ left (2 \ pi f_ct \ right) $ é a fase deslocada por $ -90 ^ 0 $ para obter $ A_c \ sin \ left (2 \ pi f_ct \ right) $ com a ajuda de $ -90 ^ 0 $ deslocador de fase. O modulador de produto tem duas entradas $ \ int m \ left (t \ right) dt $ e $ A_c \ sin \ left (2 \ pi f_ct \ right) $. Ele produz uma saída, que é o produto dessas duas entradas.

Isso é posteriormente multiplicado por $ 2 \ pi k_f $ colocando um bloco $ 2 \ pi k_f $ no caminho de encaminhamento. O bloco de verão tem duas entradas, que nada mais são do que os dois termos da equação NBFM. Os sinais positivos e negativos são atribuídos ao sinal da portadora e ao outro termo na entrada do bloco de verão. Finalmente, o bloco de verão produz a onda NBFM.

Geração de WBFM

Os dois métodos a seguir geram uma onda WBFM.

• Método direto
• Método indireto

Método direto

Este método é chamado de Método direto porque estamos gerando uma onda FM de banda larga diretamente. Neste método, Voltage Controlled Oscillator (VCO) é usado para gerar WBFM. O VCO produz um sinal de saída, cuja frequência é proporcional à tensão do sinal de entrada. Isso é semelhante à definição de onda FM. O diagrama de blocos da geração da onda WBFM é mostrado na figura a seguir.

Aqui, o sinal modulante $ m \ left (t \ right) $ é aplicado como uma entrada do oscilador controlado por tensão (VCO). O VCO produz uma saída, que nada mais é do que o WBFM.

$$ f_i \: \ alpha \: m \ left (t \ right) $$

$$ \ Rightarrow f_i = f_c + k_fm \ left (t \ right) $$

Onde,

$ f_i $ é a frequência instantânea da onda WBFM.

Método Indireto

Este método é chamado de Método Indireto porque estamos gerando uma onda FM de banda larga indiretamente. Isso significa que primeiro geraremos a onda NBFM e depois com a ajuda de multiplicadores de frequência obteremos a onda WBFM. O diagrama de blocos de geração da onda WBFM é mostrado na figura a seguir.

Este diagrama de blocos contém principalmente dois estágios. Na primeira etapa, a onda NBFM será gerada usando o modulador NBFM. Vimos o diagrama de blocos do modulador NBFM no início deste capítulo. Sabemos que o índice de modulação da onda NBFM é menor que um. Portanto, para obter o índice de modulação necessário (maior que um) da onda FM, escolha o valor do multiplicador de frequência corretamente.

Frequency multiplieré um dispositivo não linear, que produz um sinal de saída cuja freqüência é 'n' vezes a freqüência do sinal de entrada. Onde, 'n' é o fator de multiplicação.

Se a onda NBFM cujo índice de modulação $ \ beta $ é menor que 1 é aplicada como a entrada do multiplicador de frequência, então o multiplicador de frequência produz um sinal de saída, cujo índice de modulação é 'n' vezes $ \ beta $ e a frequência também 'n 'vezes a frequência da onda WBFM.

Às vezes, podemos exigir vários estágios de multiplicador de frequência e mixadores para aumentar o desvio de frequência e o índice de modulação da onda FM.

Neste capítulo, vamos discutir sobre os demoduladores que demodulam a onda FM. Os dois métodos a seguir desmodulam a onda FM.

• Método de discriminação de frequência
• Método de discriminação de fase

Método de Discriminação de Frequência

Sabemos que a equação da onda FM é

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$

Diferencie a equação acima em relação a 't'.

$$ \ frac {ds \ left (t \ right)} {dt} = -A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ right) \ right) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$

Podemos escrever, $ - \ sin \ theta $ como $ \ sin \ left (\ theta -180 ^ 0 \ right) $.

$$ \ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ right) \ right) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt-180 ^ 0 \ right) $$

$$ \ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c \ right) \ left [1+ \ left (\ frac {k_f} {k_c} \ right) m \ left ( t \ direita) \ direita] \ sin \ esquerda (2 \ pi f_ct + 2 \ pi k_f \ int m \ esquerda (t \ direita) dt-180 ^ 0 \ direita) $$

Na equação acima, o termo amplitude se assemelha ao envelope da onda AM e o termo ângulo se assemelha ao ângulo da onda FM. Aqui, nosso requisito é o sinal de modulação $ m \ left (t \ right) $. Portanto, podemos recuperá-lo do envelope da onda AM.

A figura a seguir mostra o diagrama de blocos do demodulador FM usando o método de discriminação de frequência.

Este diagrama de blocos consiste no diferenciador e no detector de envelope. O diferenciador é usado para converter a onda FM em uma combinação de onda AM e onda FM. Isso significa que ele converte as variações de frequência da onda FM nas variações de tensão (amplitude) correspondentes da onda AM. Conhecemos o funcionamento do detector de envelope. Ele produz a saída demodulada da onda AM, que nada mais é do que o sinal modulante.

Método de Discriminação de Fase

A figura a seguir mostra o diagrama de blocos do demodulador FM usando o método de discriminação de fase.

Este diagrama de blocos consiste no multiplicador, o filtro passa-baixo e o oscilador controlado por tensão (VCO). O VCO produz um sinal de saída $ v \ left (t \ right) $, cuja frequência é proporcional à tensão do sinal de entrada $ d \ left (t \ right) $. Inicialmente, quando o sinal $ d \ left (t \ right) $ é zero, ajuste o VCO para produzir um sinal de saída $ v \ left (t \ right) $, tendo uma frequência portadora e $ -90 ^ 0 $ mudança de fase com relação ao sinal da portadora.

A onda FM $ s \ left (t \ right) $ e a saída VCO $ v \ left (t \ right) $ são aplicadas como entradas do multiplicador. O multiplicador produz uma saída, tendo um componente de alta frequência e um componente de baixa frequência. O filtro passa-baixa elimina o componente de alta frequência e produz apenas o componente de baixa frequência como sua saída.

Este componente de baixa frequência contém apenas a diferença de fase relacionada ao termo. Conseqüentemente, obtemos o sinal modulante $ m \ left (t \ right) $ desta saída do filtro passa-baixo.

Multiplexingé o processo de combinar vários sinais em um sinal, em um meio compartilhado. Se os sinais analógicos forem multiplexados, é chamado deanalog multiplexing. Da mesma forma, se os sinais digitais são multiplexados, então é chamado dedigital multiplexing.

A multiplexação foi desenvolvida pela primeira vez na telefonia. Vários sinais foram combinados para enviar por meio de um único cabo. O processo de multiplexação divide um canal de comunicação em vários canais lógicos, atribuindo a cada um um sinal de mensagem diferente ou um fluxo de dados a ser transferido. O dispositivo que faz multiplexação pode ser chamado deMultiplexer ou MUX.

O processo reverso, ou seja, extrair o número de canais de um, que é feito no receptor, é denominado como de-multiplexing. O dispositivo que faz a desmultiplexação pode ser chamado dede-multiplexer ou DEMUX.

As figuras a seguir ilustram o conceito de MUX e DEMUX. Seu uso principal é no campo das comunicações.

Tipos de multiplexadores

Existem basicamente dois tipos de multiplexadores: analógico e digital. Eles são divididos em Multiplexação por Divisão de Frequência (FDM), Multiplexação por Divisão de Comprimento de Onda (WDM) e Multiplexação por Divisão de Tempo (TDM). A figura a seguir dá uma ideia detalhada sobre essa classificação.

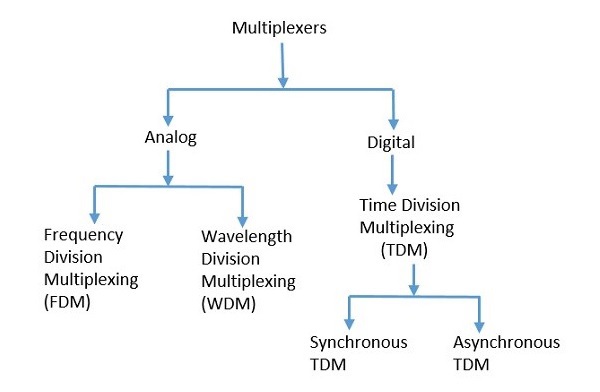
Existem muitos tipos de técnicas de multiplexação. Destes, temos os principais tipos com classificação geral, mencionados na figura acima. Vamos dar uma olhada neles individualmente.

Multiplexação Analógica

Os sinais usados ​​nas técnicas de multiplexação analógica são analógicos por natureza. Os sinais analógicos são multiplexados de acordo com sua frequência (FDM) ou comprimento de onda (WDM).

Multiplexação por divisão de frequência

Na multiplexação analógica, a técnica mais usada é a Multiplexação por Divisão de Freqüência (FDM). Essa técnica usa várias frequências para combinar fluxos de dados, para enviá-los em um meio de comunicação, como um único sinal.

Example - Um transmissor de televisão tradicional, que envia vários canais por meio de um único cabo, usa FDM.

Wavelength Division Multiplexing

A multiplexação por divisão de comprimento de onda (WDM) é uma técnica analógica, na qual muitos fluxos de dados de diferentes comprimentos de onda são transmitidos no espectro de luz. Se o comprimento de onda aumenta, a frequência do sinal diminui. Um prisma, que pode transformar diferentes comprimentos de onda em uma única linha, pode ser usado na saída do MUX e na entrada do DEMUX.

Example - As comunicações de fibra óptica usam a técnica WDM, para mesclar diferentes comprimentos de onda em uma única luz para comunicação.

Multiplexação Digital

O termo digital representa os bits discretos de informação. Assim, os dados disponíveis estão na forma de quadros ou pacotes, que são discretos.

Multiplexação por divisão de tempo

Em Time Division Multiplexing (TDM), o período de tempo é dividido em slots. Essa técnica é usada para transmitir um sinal em um único canal de comunicação, atribuindo um slot para cada mensagem.

A Multiplexação por Divisão de Tempo (TDM) pode ser classificada em TDM Síncrona e TDM Assíncrona.

TDM síncrono

No TDM síncrono, a entrada é conectada a um quadro. Se houver 'n' número de conexões, o quadro será dividido em 'n' intervalos de tempo. Um slot é alocado para cada linha de entrada.

Nesta técnica, a taxa de amostragem é comum para todos os sinais e, portanto, a mesma entrada de relógio é fornecida. O MUX aloca osame slot para cada dispositivo em todos os momentos.

TDM assíncrono

No TDM assíncrono, a taxa de amostragem é diferente para cada um dos sinais e um clock comum não é necessário. Se o dispositivo alocado para um intervalo de tempo não transmitir nada e ficar ocioso, esse intervalo pode serallotted to another dispositivo, ao contrário do síncrono

Este tipo de TDM é usado em redes de modo de transferência assíncrona.

De-Multiplexer

Desmultiplexadores são usados ​​para conectar uma única fonte a vários destinos. Este processo é o processo reverso da multiplexação. Conforme mencionado anteriormente, ele é usado principalmente nos receptores. DEMUX tem muitos aplicativos. É usado em receptores nos sistemas de comunicação. É usado na unidade aritmética e lógica em computadores para fornecer energia e passar comunicação, etc.

Desmultiplexadores são usados ​​como conversores serial para paralelo. Os dados seriais são fornecidos como entrada para DEMUX em intervalo regular e um contador é anexado a ele para controlar a saída do de-multiplexador.

Tanto os multiplexadores quanto os de-multiplexadores desempenham um papel importante nos sistemas de comunicação, tanto no transmissor quanto no receptor.

Em qualquer sistema de comunicação, durante a transmissão do sinal ou durante a recepção do sinal, algum sinal indesejado é introduzido na comunicação, tornando-a desagradável para o receptor e questionando a qualidade da comunicação. Essa perturbação é chamada deNoise.

O que é ruído?

O ruído é um unwanted signal, que interfere com o sinal de mensagem original e corrompe os parâmetros do sinal de mensagem. Essa alteração no processo de comunicação, faz com que a mensagem seja alterada. Provavelmente entra no canal ou no receptor.

O sinal de ruído pode ser compreendido observando a figura a seguir.

Portanto, entende-se que o ruído é algum sinal que não tem padrão e nenhuma frequência ou amplitude constante. É bastante aleatório e imprevisível. Normalmente são tomadas medidas para reduzi-lo, embora não possa ser completamente eliminado.

Os exemplos mais comuns de ruído são -

• Som assobio em receptores de rádio

• Som de zumbido em meio a conversas telefônicas

• Cintilação em receptores de televisão, etc.

Tipos de ruído

A classificação do ruído é feita em função do tipo de fonte, do efeito que mostra ou da relação que tem com o receptor, etc.

Existem duas maneiras principais de produzir ruído. Um é através de algunsexternal source enquanto o outro é criado por um internal source, dentro da seção do receptor.

Fonte externa

Este ruído é produzido pelas fontes externas, o que pode ocorrer no meio ou canal de comunicação normalmente. Este ruído não pode ser totalmente eliminado. A melhor maneira é evitar que o ruído afete o sinal.

Exemplos

Os exemplos mais comuns deste tipo de ruído são

• Ruído atmosférico (devido a irregularidades na atmosfera).

• Ruído extraterrestre, como ruído solar e ruído cósmico.

• Ruído industrial.

Fonte Interna

Este ruído é produzido pelos componentes do receptor durante o funcionamento. Os componentes dos circuitos, devido ao funcionamento contínuo, podem produzir poucos tipos de ruído. Esse ruído é quantificável. Um projeto de receptor adequado pode diminuir o efeito desse ruído interno.

Examples

Os exemplos mais comuns deste tipo de ruído são

• Ruído de agitação térmica (ruído Johnson ou ruído elétrico)

• Ruído de disparo (devido ao movimento aleatório de elétrons e lacunas)

• Ruído do tempo de trânsito (durante a transição)

• Ruídos diversos são outro tipo de ruído que inclui tremulação, efeito de resistência e ruído gerado pelo mixer, etc.

Efeitos do ruído

O ruído é um recurso inconveniente, que afeta o desempenho do sistema. A seguir estão os efeitos do ruído.

O ruído limita a faixa operacional dos sistemas

O ruído indiretamente coloca um limite no sinal mais fraco que pode ser amplificado por um amplificador. O oscilador no circuito do mixer pode limitar sua frequência por causa do ruído. A operação de um sistema depende da operação de seus circuitos. O ruído limita o menor sinal que um receptor é capaz de processar.

O ruído afeta a sensibilidade dos receptores

A sensibilidade é a quantidade mínima de sinal de entrada necessária para obter a saída de qualidade especificada. O ruído afeta a sensibilidade de um sistema receptor, o que eventualmente afeta a saída.

Neste capítulo, vamos calcular as relações entre sinal e ruído e a figura de méritos de várias ondas moduladas, que são demoduladas no receptor.

A relação sinal-ruído

Signal-to-Noise Ratio (SNR)é a relação entre a potência do sinal e a potência do ruído. Quanto maior o valor de SNR, maior será a qualidade da saída recebida.

A relação sinal-ruído em diferentes pontos pode ser calculada usando as seguintes fórmulas.

Input SNR = $ \ left (SNR \ right) _I = \ frac {Média \: \: potência \: \: de \: \: modulando \: \: sinal} {Média \: \: potência \: \: de \: \: ruído \: \: at \: \: entrada} $

Output SNR = $ \ left (SNR \ right) _O = \ frac {Média \: \: potência \: \: de \: \: demodulado \: \: sinal} {Média \: \: potência \: \: de \: \: ruído \: \: at \: \: saída} $

Channel SNR = $ \ left (SNR \ right) _C = \ frac {Média \: \: potência \: \: de \: \: modulado \: \: sinal} {Média \: \: potência \: \: de \: \: ruído \: \: em \: \: mensagem \: \: largura de banda} $

Figura de mérito

A proporção de SNR de saída e SNR de entrada pode ser denominada como Figure of Merit. É denotado porF. Ele descreve o desempenho de um dispositivo.

$$ F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _I} $$

Figura de mérito de um receptor é

$$ F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _C} $$

É assim porque, para um receptor, o canal é a entrada.

Cálculos SNR no Sistema AM

Considere o seguinte modelo de receptor do sistema AM para analisar o ruído.

Sabemos que a onda modulada em amplitude (AM) é

$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$

A potência média da onda AM é

$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2}} {2} + \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2} $ $

$$ \ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} P \ right)} {2} $$

A potência média de ruído na largura de banda da mensagem é

$$ P_ {nc} = WN_0 $$

Substitua, esses valores em channel SNR Fórmula

$$ \ left (SNR \ right) _ {C, AM} = \ frac {Média \: \: Potência \: \: de \: \: AM \: \: Onda} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: mensagem \: \: largura de banda} $$

$$ \ Rightarrow \ left (SNR \ right) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P } {2WN_0} $$

Onde,

• P é a potência do sinal de mensagem = $ \ frac {{A_ {m}} ^ {2}} {2} $

• W é a largura de banda da mensagem

Suponha que o ruído da passagem de banda seja misturado com a onda AM no canal, conforme mostrado na figura acima. Esta combinação é aplicada na entrada do demodulador AM. Portanto, a entrada do demodulador AM é.

$$ v \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right) $$

$ \ Rightarrow v \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) + $

$ \ left [n_1 \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $

$ \ Rightarrow v \ left (t \ right) = \ left [A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $

Onde $ n_I \ left (t \ right) $ e $ n_Q \ left (t \ right) $ estão em fase e componentes de fase em quadratura do ruído.

A saída do demodulador AM nada mais é do que o envelope do sinal acima.

$$ d \ left (t \ right) = \ sqrt {\ left [A_c + A_cK_am \ left (t \ right) + n_I \ left (t \ right) \ right] ^ 2 + \ left (n_Q \ left (t \ right) \ right) ^ 2} $$

$$ \ Rightarrow d \ left (t \ right) \ aprox A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) $$

A potência média do sinal demodulado é

$$ P_m = \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2} $$

A potência média de ruído na saída é

$$ P_no = WN_0 $$

Substitua, esses valores em output SNR Fórmula.

$$ \ left (SNR \ right) _ {O, AM} = \ frac {Média \: \: Potência \: \: de \: \: demodulado \: \: sinal} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: Saída} $$

$$ \ Rightarrow \ left (SNR \ right) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0} $$

Substitua, os valores em Figure of merit da fórmula do receptor AM.

$$ F = \ frac {\ left (SNR \ right) _ {O, AM}} {\ left (SNR \ right) _ {C, AM}} $$

$$ \ Rightarrow F = \ left (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ right) / \ left (\ frac {{A_ { c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P} {2WN_0} \ right) $$

$$ \ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P} $$

Portanto, a Figura de mérito do receptor AM é menor que um.

Cálculos SNR no Sistema DSBSC

Considere o seguinte modelo de receptor do sistema DSBSC para analisar o ruído.

Sabemos que a onda modulada DSBSC é

$$ s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$

A potência média da onda modulada DSBSC é

$$ P_s = \ left (\ frac {A_cm \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2} $$

A potência média de ruído na largura de banda da mensagem é

$$ P_ {nc} = WN_0 $$

Substitua, esses valores em channel SNR Fórmula.

$$ \ left (SNR \ right) _ {C, DSBSC} = \ frac {Média \: \: Potência \: \: de \: \: DSBSC \: \: modulado \: \: onda} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: mensagem \: \: largura de banda} $$

$$ \ Rightarrow \ left (SNR \ right) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$

Suponha que o ruído de passagem de banda seja misturado com a onda modulada DSBSC no canal, conforme mostrado na figura acima. Essa combinação é aplicada como uma das entradas para o modulador de produto. Portanto, a entrada deste modulador de produto é

$$ v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right) $$

$$ \ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ left [n_I \ left (t \ right) \ cos \ left ( 2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $$

$$ \ Rightarrow v_1 \ left (t \ right) = \ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$

O oscilador local gera o sinal da portadora $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $. Este sinal é aplicado como outra entrada para o modulador do produto. Portanto, o modulador de produto produz uma saída, que é o produto de $ v_1 \ left (t \ right) $ e $ c \ left (t \ right) $.

$$ v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right) $$

Substitua os valores $ v_1 \ left (t \ right) $ e $ c \ left (t \ right) $ na equação acima.

$$ \ Rightarrow v_2 \ left (t \ right) = \ left (\ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right ) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) $$

$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos ^ 2 \ left (2 \ pi f_ct \ right ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right) $$

$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left ( 4 \ pi f_ct \ right)} {2} \ right) -n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2} $$

Quando o sinal acima é aplicado como uma entrada para o filtro passa-baixo, obteremos a saída do filtro passa-baixo como

$$ d \ left (t \ right) = \ frac {\ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right]} {2} $$

A potência média do sinal demodulado é

$$ P_m = \ left (\ frac {A_cm \ left (t \ right)} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 } $$

A potência média de ruído na saída é

$$ P_ {no} = \ frac {WN_0} {4} $$

Substitua, esses valores em output SNR Fórmula.

$$ \ left (SNR \ right) _ {O, DSBSC} = \ frac {Média \: \: Potência \: \: de \: \: demodulado \: \: sinal} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: Saída} $$

$$ \ Rightarrow \ left (SNR \ right) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ right) / \ left (\ frac {WN_0 } {4} \ right) = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$

Substitua, os valores em Figure of merit da fórmula do receptor DSBSC.

$$ F = \ frac {\ left (SNR \ right) _ {O, DSBSC}} {\ left (SNR \ right) _ {C, DSBSC}} $$

$$ \ Rightarrow F = \ left (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right) / \ left (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ right) $$

$$ \ Rightarrow F = 1 $$

Portanto, a Figura de mérito do receptor DSBSC é 1.

Cálculos SNR no Sistema SSBSC

Considere o seguinte modelo de receptor do sistema SSBSC para analisar o ruído.

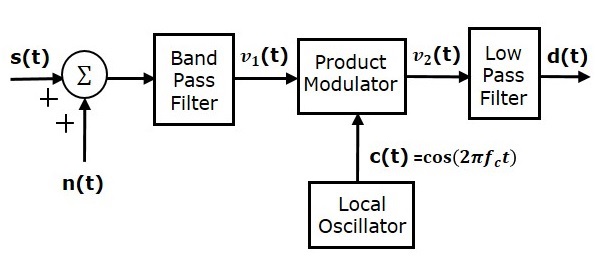
Sabemos que a onda modulada SSBSC com banda lateral inferior é

$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$

A potência média da onda modulada SSBSC é

$$ P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8} $$

A potência média de ruído na largura de banda da mensagem é

$$ P_ {nc} = WN_0 $$

Substitua, esses valores em channel SNR Fórmula.

$$ \ left (SNR \ right) _ {C, SSBSC} = \ frac {Média \: \: Potência \: \: de \: \: SSBSC \: \: modulado \: \: onda} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: mensagem \: \: largura de banda} $$

$$ \ Rightarrow \ left (SNR \ right) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$

Suponha que o ruído da passagem de banda seja misturado com a onda modulada SSBSC no canal, conforme mostrado na figura acima. Essa combinação é aplicada como uma das entradas para o modulador de produto. Portanto, a entrada deste modulador de produto é

$$ v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right) $$

$$ v_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] + n_I \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$

O oscilador local gera o sinal da portadora $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $. Este sinal é aplicado como outra entrada para o modulador do produto. Portanto, o modulador de produto produz uma saída, que é o produto de $ v_1 \ left (t \ right) $ e $ c \ left (t \ right) $.

$$ v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right) $$

Substitua os valores $ v_1 \ left (t \ right) $ e $ c \ left (t \ right) $ na equação acima.

$ \ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct) - $

$ n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct) $

$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ direita) + $

$ n_I \ left (t \ right) \ cos ^ 2 \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right) $

$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} + $

$ n_I \ left (t \ right) \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right) - n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2} $

Quando o sinal acima é aplicado como uma entrada para o filtro passa-baixo, obteremos a saída do filtro passa-baixo como

$$ d \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ right) + \ frac {n_I \ left (t \ right)} {2} $$

A potência média do sinal demodulado é

$$ P_m = \ left (\ frac {A_mA_c} {4 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} $$

A potência média de ruído na saída é

$$ P_ {no} = \ frac {WN_0} {4} $$

Substitua, esses valores em output SNR Fórmula

$$ \ left (SNR \ right) _ {O, SSBSC} = \ frac {Média \: \: Potência \: \: de \: \: demodulado \: \: sinal} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: saída} $$

$$ \ Rightarrow \ left (SNR \ right) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ right ) / \ left (\ frac {WN_0} {4} \ right) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$

Substitua, os valores em Figure of merit da fórmula do receptor SSBSC

$$ F = \ frac {\ left (SNR \ right) _ {O, SSBSC}} {\ left (SNR \ right) _ {C, SSBSC}} $$

$$ F = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) / \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) $$

$$ F = 1 $$

Portanto, a Figura de mérito do receptor SSBSC é 1.

A antena presente no final da seção do transmissor, transmite a onda modulada. Neste capítulo, vamos discutir sobre os transmissores AM e FM.

Transmissor AM

O transmissor AM recebe o sinal de áudio como uma entrada e fornece uma onda modulada em amplitude para a antena como uma saída a ser transmitida. O diagrama de blocos do transmissor AM é mostrado na figura a seguir.

O funcionamento do transmissor AM pode ser explicado como segue.

• O sinal de áudio da saída do microfone é enviado para o pré-amplificador, que aumenta o nível do sinal de modulação.

• O oscilador de RF gera o sinal da portadora.

• Tanto o sinal modulante quanto a portadora são enviados ao modulador AM.

• O amplificador de potência é usado para aumentar os níveis de potência da onda AM. Esta onda é finalmente passada para a antena para ser transmitida.

Transmissor FM

O transmissor FM é a unidade inteira, que recebe o sinal de áudio como uma entrada e entrega a onda FM à antena como uma saída a ser transmitida. O diagrama de blocos do transmissor FM é mostrado na figura a seguir.

O funcionamento do transmissor FM pode ser explicado a seguir.

• O sinal de áudio da saída do microfone é enviado para o pré-amplificador, que aumenta o nível do sinal de modulação.

• Este sinal é então passado para o filtro passa-alta, que atua como uma rede pré-ênfase para filtrar o ruído e melhorar a relação sinal-ruído.

• Este sinal é posteriormente passado para o circuito modulador FM.

• O circuito oscilador gera uma portadora de alta frequência, que é enviada ao modulador junto com o sinal modulante.

• Vários estágios do multiplicador de frequência são usados ​​para aumentar a frequência de operação. Mesmo assim, a potência do sinal não é suficiente para transmitir. Portanto, um amplificador de potência RF é usado no final para aumentar a potência do sinal modulado. Esta saída modulada FM é finalmente passada para a antena para ser transmitida.

A antena presente no início da seção receptora, recebe a onda modulada. Primeiro, vamos discutir os requisitos de um receptor.

Requisitos de um receptor

O receptor AM recebe a onda AM e a demodula usando o detector de envelope. Da mesma forma, o receptor FM recebe as ondas FM e as demodula usando o método de discriminação de frequência. A seguir estão os requisitos do receptor AM e FM.

• Deve ser econômico.

• Deve receber as ondas moduladas correspondentes.

• O receptor deve ser capaz de sintonizar e amplificar a estação desejada.

• Deve ter a capacidade de rejeitar as estações indesejadas.

• A demodulação deve ser feita em todos os sinais da estação, independentemente da frequência do sinal da portadora.

Para que esses requisitos sejam atendidos, o circuito do sintonizador e o circuito do mixer devem ser muito eficazes. O procedimento de mixagem de RF é um fenômeno interessante.

Mixagem RF

A unidade de mistura de RF desenvolve um Intermediate Frequency (IF) para o qual qualquer sinal recebido é convertido, de modo a processar o sinal de forma eficaz.

O RF Mixer é um estágio importante no receptor. Dois sinais de frequências diferentes são obtidos onde um nível de sinal afeta o nível do outro sinal, para produzir a saída mista resultante. Os sinais de entrada e a saída resultante do mixer são ilustrados nas figuras a seguir.

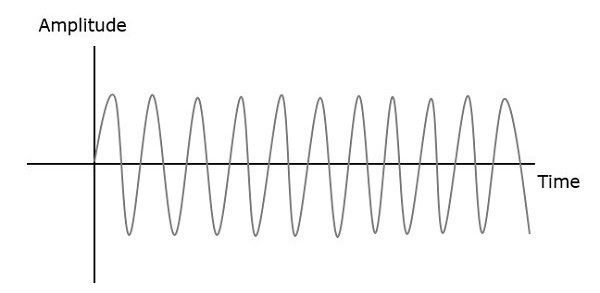
Sejam a primeira e a segunda frequências de sinal $ f_1 $ e $ f_2 $. Se esses dois sinais forem aplicados como entradas do mixer RF, ele produzirá um sinal de saída, com frequências de $ f_1 + f_2 $ e $ f_1-f_2 $.

Se isso for observado no domínio da frequência, o padrão se parece com a figura a seguir.

Nesse caso, $ f_1 $ é maior que $ f_2 $. Portanto, a saída resultante tem as frequências $ f_1 + f_2 $ e $ f_1-f_2 $. Da mesma forma, se $ f_2 $ é maior que $ f_1 $, então a saída resultante terá as frequências $ f_1 + f_2 $ e $ f_1-f_2 $.

Receptor AM

O receptor AM super heteródino pega a onda modulada em amplitude como uma entrada e produz o sinal de áudio original como uma saída. Selectivity é a capacidade de selecionar um determinado sinal, rejeitando os outros. Sensitivity é a capacidade de detectar o sinal de RF e demodulá-lo, enquanto está no nível de potência mais baixo.

Os rádios amadores são os primeiros receptores de rádio. No entanto, eles têm desvantagens, como baixa sensibilidade e seletividade. Para superar essas desvantagens,super heterodynereceptor foi inventado. O diagrama de blocos do receptor AM é mostrado na figura a seguir.

Seção de sintonizador RF

A onda modulada em amplitude recebida pela antena é primeiro passada para o tuner circuitatravés de um transformador. O circuito do sintonizador nada mais é do que um circuito LC, que também é chamado deresonant ou tank circuit. Seleciona a frequência desejada pelo receptor AM. Ele também ajusta o oscilador local e o filtro de RF ao mesmo tempo.

Mixer RF

O sinal da saída do sintonizador é enviado para o RF-IF converter, que atua como um mixer. Possui um oscilador local, que produz uma frequência constante. O processo de mixagem é feito aqui, tendo o sinal recebido como uma entrada e a frequência do oscilador local como outra entrada. A saída resultante é uma mistura de duas frequências $ \ left [\ left (f_1 + f_2 \ right), \ left (f_1-f_2 \ right) \ right] $ produzido pelo mixer, que é chamado deIntermediate Frequency (IF).

A produção de IF auxilia na demodulação de qualquer sinal de estação com qualquer frequência portadora. Portanto, todos os sinais são traduzidos para uma frequência de portadora fixa para seletividade adequada.

Filtro IF

O filtro de frequência intermediário é um filtro passa-banda, que passa a frequência desejada. Ele elimina todos os outros componentes de frequência indesejados presentes nele. Esta é a vantagem do filtro IF, que permite apenas a frequência IF.

Demodulator AM

A onda AM recebida é agora demodulada usando o desmodulador AM. Este demodulador usa o processo de detecção de envelope para receber o sinal de modulação.

Amplificador de áudio

Este é o estágio do amplificador de potência, que é usado para amplificar o sinal de áudio detectado. O sinal processado é fortalecido para ser eficaz. Este sinal é passado para o alto-falante para obter o sinal de som original.

Receptor FM

O diagrama de blocos do receptor FM é mostrado na figura a seguir.

Este diagrama de blocos do receptor FM é semelhante ao diagrama de blocos do receptor AM. O limitador de amplitude de dois blocos e a rede sem ênfase estão incluídos antes e depois do demodulador FM. O funcionamento dos blocos restantes é igual ao do receptor AM.

Sabemos que na modulação FM, a amplitude da onda FM permanece constante. No entanto, se algum ruído for adicionado à onda FM no canal, devido a isso, a amplitude da onda FM pode variar. Assim, com a ajuda deamplitude limiter podemos manter a amplitude da onda FM constante, removendo os picos indesejados do sinal de ruído.

No transmissor FM, vimos a rede de pré-ênfase (filtro passa-alto), que está presente antes do modulador FM. Isso é usado para melhorar o SNR do sinal de áudio de alta frequência. O processo reverso de pré-ênfase é conhecido comode-emphasis. Assim, neste receptor FM, a rede sem ênfase (filtro passa-baixa) é incluída após o demodulador FM. Este sinal é passado para o amplificador de áudio para aumentar o nível de potência. Finalmente, obtemos o sinal de som original do alto-falante.

Até agora, discutimos sobre a modulação de onda contínua. Discutiremos sobre modulação de pulso no próximo capítulo. Essas técnicas de modulação de pulso lidam com sinais discretos. Então, agora vamos ver como converter um sinal de tempo contínuo em um sinal discreto.

O processo de conversão de sinais de tempo contínuo em sinais de tempo discretos equivalentes pode ser denominado como Sampling. Um certo instante de dados é continuamente amostrado no processo de amostragem.

A figura a seguir mostra um sinal de tempo contínuo x(t) e o sinal amostrado correspondente x_s(t). Quandox(t) é multiplicado por um trem de impulso periódico, o sinal amostrado x_s(t) é obtido.

UMA sampling signal é um trem periódico de pulsos, tendo amplitude unitária, amostrado em intervalos iguais de tempo $ T_s $, que é chamado sampling time. Esses dados são transmitidos nos instantes de tempo $ T_s $ e o sinal da portadora é transmitido no tempo restante.

Taxa de amostragem

Para discretizar os sinais, a lacuna entre as amostras deve ser corrigida. Essa lacuna pode ser denominada como o período de amostragem $ T_s $. Recíproco do período de amostragem é conhecido comosampling frequency ou sampling rate $f_s$.

Matematicamente, podemos escrever como

$$ f_s = \ frac {1} {T_s} $$

Onde,

$ f_s $ é a frequência de amostragem ou a taxa de amostragem

$ T_s $ é o período de amostragem

Teorema de Amostragem

A taxa de amostragem deve ser tal que os dados no sinal de mensagem não sejam perdidos nem sobrepostos. osampling theorem afirma que, “um sinal pode ser reproduzido exatamente se for amostrado na taxa $ f_s $, que é maior ou igual a duas vezes a frequência máxima do sinal dado W. ”

Matematicamente, podemos escrever como

$$ f_s \ geq 2W $$

Onde,

• $ f_s $ é a taxa de amostragem

• $ W $ é a frequência mais alta do sinal fornecido

Se a taxa de amostragem for igual a duas vezes a frequência máxima do sinal W dado, então ele é chamado de Nyquist rate.

O teorema da amostragem, que também é chamado de Nyquist theorem, fornece a teoria da taxa de amostragem suficiente em termos de largura de banda para a classe de funções que são limitadas por banda.

Para sinal de tempo contínuo x(t), que é limitado por banda no domínio da frequência é representado conforme mostrado na figura a seguir.

Se o sinal for amostrado acima da taxa de Nyquist, o sinal original pode ser recuperado. A figura a seguir explica um sinal, se amostrado a uma taxa maior do que2w no domínio da frequência.

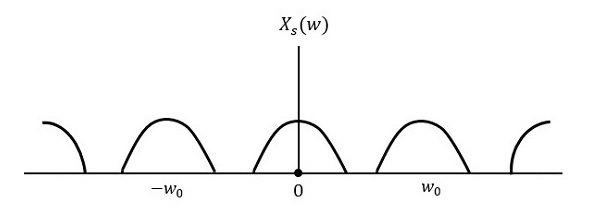
Se o mesmo sinal for amostrado a uma taxa menor que 2w, então o sinal amostrado seria semelhante à figura a seguir.

Podemos observar a partir do padrão acima que há sobreposição de informações, o que leva à confusão e perda de informações. Este fenômeno indesejado de sobreposição é chamado deAliasing.

O aliasing pode ser referido como "o fenômeno de um componente de alta frequência no espectro de um sinal, assumindo a identidade de um componente de baixa frequência no espectro de sua versão amostrada".

Portanto, a taxa de amostragem do sinal é escolhida como taxa de Nyquist. Se a taxa de amostragem for igual a duas vezes a maior frequência do sinal dadoW, então o sinal amostrado seria semelhante à figura a seguir.

Neste caso, o sinal pode ser recuperado sem nenhuma perda. Portanto, esta é uma boa taxa de amostragem.

Após a modulação de onda contínua, a próxima divisão é a modulação de pulso. Neste capítulo, vamos discutir as seguintes técnicas de modulação de pulso analógico.

• Modulação de amplitude de pulso
• Modulação de largura de pulso
• Modulação de posição de pulso

Modulação de amplitude de pulso

No Pulse Amplitude Modulation (PAM) técnica, a amplitude da portadora de pulso varia, que é proporcional à amplitude instantânea do sinal de mensagem.

O sinal modulado por amplitude de pulso seguirá a amplitude do sinal original, à medida que o sinal traça o caminho de toda a onda. No PAM natural, um sinal amostrado na taxa de Nyquist pode ser reconstruído, passando-o por um eficienteLow Pass Filter (LPF) com frequência de corte exata.

As figuras a seguir explicam a modulação de amplitude de pulso.

Embora o sinal PAM seja passado por um LPF, ele não pode recuperar o sinal sem distorção. Portanto, para evitar esse ruído, use a amostragem plana. O sinal PAM de topo plano é mostrado na figura a seguir.

Flat-top samplingé o processo no qual, o sinal amostrado pode ser representado em pulsos para os quais a amplitude do sinal não pode ser alterada em relação ao sinal analógico a ser amostrado. Os topos da amplitude permanecem planos. Este processo simplifica o projeto do circuito.

Modulação de largura de pulso

No Pulse Width Modulation (PWM) ou a técnica de Modulação de Duração de Pulso (PDM) ou Modulação de Tempo de Pulso (PTM), a largura ou a duração ou o tempo da portadora de pulso varia, que é proporcional à amplitude instantânea do sinal de mensagem.

A largura do pulso varia neste método, mas a amplitude do sinal permanece constante. Limitadores de amplitude são usados ​​para tornar a amplitude do sinal constante. Esses circuitos cortam a amplitude a um nível desejado e, portanto, o ruído é limitado.

A figura a seguir explica os tipos de modulações de largura de pulso.

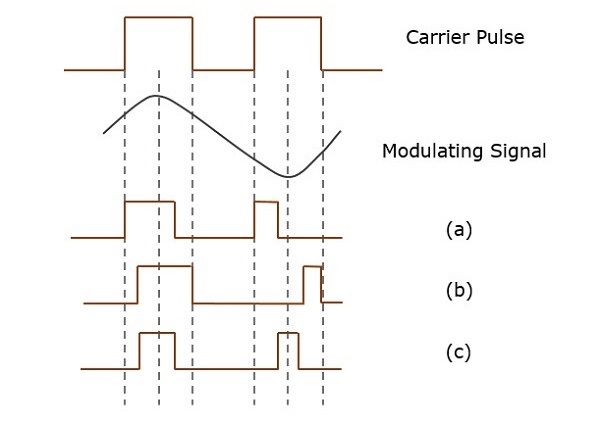
Existem três tipos de PWM.

• Sendo a borda dianteira do pulso constante, a borda traseira varia de acordo com o sinal de mensagem. A forma de onda para este tipo de PWM é denotada como (a) na figura acima.

• Sendo a borda posterior do pulso constante, a borda dianteira varia de acordo com o sinal de mensagem. A forma de onda para este tipo de PWM é denotada como (b) na figura acima.

• Sendo o centro do pulso constante, a borda de ataque e a borda de fuga variam de acordo com o sinal de mensagem. A forma de onda para este tipo de PWM é denotada como (c) mostrado na figura acima.

Modulação de posição de pulso

Pulse Position Modulation (PPM) é um esquema de modulação analógica em que a amplitude e a largura dos pulsos são mantidas constantes, enquanto a posição de cada pulso, em relação à posição de um pulso de referência, varia de acordo com o valor amostrado instantâneo do sinal de mensagem.

O transmissor deve enviar pulsos de sincronização (ou simplesmente pulsos de sincronização) para manter o transmissor e o receptor em sincronia. Esses pulsos de sincronização ajudam a manter a posição dos pulsos. As figuras a seguir explicam a modulação de posição de pulso.

A modulação da posição de pulso é feita de acordo com o sinal modulado por largura de pulso. Cada borda de fuga do sinal modulado por largura de pulso se torna o ponto de partida para pulsos no sinal PPM. Portanto, a posição desses pulsos é proporcional à largura dos pulsos PWM.

Vantagem

Como a amplitude e a largura são constantes, a potência manuseada também é constante.

Desvantagem

A sincronização entre o transmissor e o receptor é imprescindível.

Comparação entre PAM, PWM e PPM

A tabela a seguir apresenta a comparação entre três técnicas de modulação.

PAM	PWM	PPM
A amplitude é variada	A largura é variada	A posição é variada
A largura de banda depende da largura do pulso	A largura de banda depende do tempo de subida do pulso	A largura de banda depende do tempo de subida do pulso
A potência do transmissor instantâneo varia com a amplitude dos pulsos	A potência do transmissor instantâneo varia com a amplitude e a largura dos pulsos	A potência do transmissor instantâneo permanece constante com a largura dos pulsos
A complexidade do sistema é alta	A complexidade do sistema é baixa	A complexidade do sistema é baixa
A interferência de ruído é alta	A interferência de ruído é baixa	A interferência de ruído é baixa
É semelhante à modulação de amplitude	É semelhante à modulação de frequência	É semelhante à modulação de fase

Transduceré um dispositivo que converte energia de uma forma para outra. Neste capítulo, vamos discutir sobre os transdutores usados ​​em sistemas de comunicação.

Por que precisamos de transdutores?

No mundo real, a comunicação entre quaisquer duas pessoas próximas ocorre com a ajuda de ondas sonoras. Mas, se as pessoas estiverem longe, é difícil transmitir a informação sem qualquer perda usando as ondas sonoras em sua forma física.

Para superar essa dificuldade, podemos usar moduladores na seção do transmissor e demoduladores na seção do receptor. Esses moduladores e demoduladores operam com sinais elétricos. É por isso que precisamos de um dispositivo, que deve converter as ondas sonoras em sinais elétricos ou vice-versa. Esse dispositivo é conhecido como transdutor.

A seguir está um diagrama de blocos simples de um transdutor.

Este transdutor possui uma única entrada e uma única saída. Ele converte a energia presente na entrada em sua saída equivalente com outra energia. Basicamente, um transdutor converte a forma não elétrica de energia em uma forma elétrica ou vice-versa.

Tipos de transdutores

Podemos classificar os transdutores nas seguintes two types com base na colocação (posição) do transdutor em sistemas de comunicação.

• Transdutor de entrada
• Transdutor de saída

Transdutores de entrada

O transdutor presente na entrada do sistema de comunicação é conhecido como um input transducer. A seguir está o diagrama de blocos de um transdutor de entrada.

Este transdutor de entrada converte a quantidade física não elétrica em um sinal elétrico. As grandezas físicas, como som ou luz, podem ser convertidas em grandezas elétricas, como voltagem ou corrente, usando este transdutor.Example: Microfone.

O microfone é usado como o transdutor de entrada, que é colocado entre a fonte de informação e a seção do transmissor. A fonte de informação produz a informação na forma de ondas sonoras. omicrophoneconverte essas ondas sonoras em sinais elétricos com a ajuda de um diafragma. Esses sinais elétricos podem ser usados ​​para processamento posterior.

Transdutores de saída

O transdutor presente na saída do sistema de comunicação é conhecido como transdutor de saída. A seguir está o diagrama de blocos de umoutput transducer.

Este transdutor de saída converte o sinal elétrico em quantidade física não elétrica. As grandezas elétricas, como voltagem ou corrente, podem ser convertidas em grandezas físicas, como som ou luz, usando este transdutor. Example: Alto-falante.

O alto-falante é usado como o transdutor de saída, que é colocado entre a seção do receptor e o destino. O demodulador presente na seção receptora produz a saída demodulada. Então oloud speakerconverte os sinais elétricos (saída demodulada) em ondas sonoras. Portanto, a funcionalidade do alto-falante é oposta à funcionalidade do microfone.

Além dos transdutores acima, existe mais um transdutor que é usado em sistemas de comunicação. Este transdutor pode ser colocado no final da seção do transmissor ou no início da seção do receptor.Example: Antena.

Uma antena é um transdutor que converte sinais elétricos em ondas eletromagnéticas e vice-versa. Uma antena pode ser usada como umtransmitting antenna ou como um receiving antenna.

Uma antena transmissora converte sinais elétricos em ondas eletromagnéticas e as irradia. Enquanto, uma antena receptora converte ondas eletromagnéticas do feixe recebido em sinais elétricos.

Nessa comunicação bidirecional, a mesma antena pode ser usada para transmissão e recepção.