Comunicação Analógica - Cálculos SNR
Neste capítulo, vamos calcular as relações entre sinal e ruído e a figura de méritos de várias ondas moduladas, que são demoduladas no receptor.
A relação sinal-ruído
Signal-to-Noise Ratio (SNR)é a relação entre a potência do sinal e a potência do ruído. Quanto maior o valor de SNR, maior será a qualidade da saída recebida.
A relação sinal-ruído em diferentes pontos pode ser calculada usando as seguintes fórmulas.
Input SNR = $ \ left (SNR \ right) _I = \ frac {Média \: \: potência \: \: de \: \: modulando \: \: sinal} {Média \: \: potência \: \: de \: \: ruído \: \: at \: \: entrada} $
Output SNR = $ \ left (SNR \ right) _O = \ frac {Média \: \: potência \: \: de \: \: demodulado \: \: sinal} {Média \: \: potência \: \: de \: \: ruído \: \: at \: \: saída} $
Channel SNR = $ \ left (SNR \ right) _C = \ frac {Média \: \: potência \: \: de \: \: modulado \: \: sinal} {Média \: \: potência \: \: de \: \: ruído \: \: em \: \: mensagem \: \: largura de banda} $
Figura de mérito
A proporção de SNR de saída e SNR de entrada pode ser denominada como Figure of Merit. É denotado porF. Ele descreve o desempenho de um dispositivo.
$$ F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _I} $$
Figura de mérito de um receptor é
$$ F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _C} $$
É assim porque, para um receptor, o canal é a entrada.
Cálculos SNR no Sistema AM
Considere o seguinte modelo de receptor do sistema AM para analisar o ruído.

Sabemos que a onda modulada em amplitude (AM) é
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$
A potência média da onda AM é
$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2}} {2} + \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2} $ $
$$ \ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} P \ right)} {2} $$
A potência média de ruído na largura de banda da mensagem é
$$ P_ {nc} = WN_0 $$
Substitua, esses valores em channel SNR Fórmula
$$ \ left (SNR \ right) _ {C, AM} = \ frac {Média \: \: Potência \: \: de \: \: AM \: \: Onda} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: mensagem \: \: largura de banda} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P } {2WN_0} $$
Onde,
P é a potência do sinal de mensagem = $ \ frac {{A_ {m}} ^ {2}} {2} $
W é a largura de banda da mensagem
Suponha que o ruído da passagem de banda seja misturado com a onda AM no canal, conforme mostrado na figura acima. Esta combinação é aplicada na entrada do demodulador AM. Portanto, a entrada do demodulador AM é.
$$ v \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right) $$
$ \ Rightarrow v \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) + $
$ \ left [n_1 \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $
$ \ Rightarrow v \ left (t \ right) = \ left [A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $
Onde $ n_I \ left (t \ right) $ e $ n_Q \ left (t \ right) $ estão em fase e componentes de fase em quadratura do ruído.
A saída do demodulador AM nada mais é do que o envelope do sinal acima.
$$ d \ left (t \ right) = \ sqrt {\ left [A_c + A_cK_am \ left (t \ right) + n_I \ left (t \ right) \ right] ^ 2 + \ left (n_Q \ left (t \ right) \ right) ^ 2} $$
$$ \ Rightarrow d \ left (t \ right) \ aprox A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) $$
A potência média do sinal demodulado é
$$ P_m = \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2} $$
A potência média de ruído na saída é
$$ P_no = WN_0 $$
Substitua, esses valores em output SNR Fórmula.
$$ \ left (SNR \ right) _ {O, AM} = \ frac {Média \: \: Potência \: \: de \: \: demodulado \: \: sinal} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: Saída} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0} $$
Substitua, os valores em Figure of merit da fórmula do receptor AM.
$$ F = \ frac {\ left (SNR \ right) _ {O, AM}} {\ left (SNR \ right) _ {C, AM}} $$
$$ \ Rightarrow F = \ left (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ right) / \ left (\ frac {{A_ { c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P} {2WN_0} \ right) $$
$$ \ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P} $$
Portanto, a Figura de mérito do receptor AM é menor que um.
Cálculos SNR no Sistema DSBSC
Considere o seguinte modelo de receptor do sistema DSBSC para analisar o ruído.

Sabemos que a onda modulada DSBSC é
$$ s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$
A potência média da onda modulada DSBSC é
$$ P_s = \ left (\ frac {A_cm \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2} $$
A potência média de ruído na largura de banda da mensagem é
$$ P_ {nc} = WN_0 $$
Substitua, esses valores em channel SNR Fórmula.
$$ \ left (SNR \ right) _ {C, DSBSC} = \ frac {Média \: \: Potência \: \: de \: \: DSBSC \: \: modulado \: \: onda} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: mensagem \: \: largura de banda} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
Suponha que o ruído de passagem de banda seja misturado com a onda modulada DSBSC no canal, conforme mostrado na figura acima. Essa combinação é aplicada como uma das entradas para o modulador de produto. Portanto, a entrada deste modulador de produto é
$$ v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right) $$
$$ \ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ left [n_I \ left (t \ right) \ cos \ left ( 2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $$
$$ \ Rightarrow v_1 \ left (t \ right) = \ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$
O oscilador local gera o sinal da portadora $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $. Este sinal é aplicado como outra entrada para o modulador do produto. Portanto, o modulador de produto produz uma saída, que é o produto de $ v_1 \ left (t \ right) $ e $ c \ left (t \ right) $.
$$ v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right) $$
Substitua os valores $ v_1 \ left (t \ right) $ e $ c \ left (t \ right) $ na equação acima.
$$ \ Rightarrow v_2 \ left (t \ right) = \ left (\ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right ) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos ^ 2 \ left (2 \ pi f_ct \ right ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left ( 4 \ pi f_ct \ right)} {2} \ right) -n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2} $$
Quando o sinal acima é aplicado como uma entrada para o filtro passa-baixo, obteremos a saída do filtro passa-baixo como
$$ d \ left (t \ right) = \ frac {\ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right]} {2} $$
A potência média do sinal demodulado é
$$ P_m = \ left (\ frac {A_cm \ left (t \ right)} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 } $$
A potência média de ruído na saída é
$$ P_ {no} = \ frac {WN_0} {4} $$
Substitua, esses valores em output SNR Fórmula.
$$ \ left (SNR \ right) _ {O, DSBSC} = \ frac {Média \: \: Potência \: \: de \: \: demodulado \: \: sinal} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: Saída} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ right) / \ left (\ frac {WN_0 } {4} \ right) = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
Substitua, os valores em Figure of merit da fórmula do receptor DSBSC.
$$ F = \ frac {\ left (SNR \ right) _ {O, DSBSC}} {\ left (SNR \ right) _ {C, DSBSC}} $$
$$ \ Rightarrow F = \ left (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right) / \ left (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ right) $$
$$ \ Rightarrow F = 1 $$
Portanto, a Figura de mérito do receptor DSBSC é 1.
Cálculos SNR no Sistema SSBSC
Considere o seguinte modelo de receptor do sistema SSBSC para analisar o ruído.
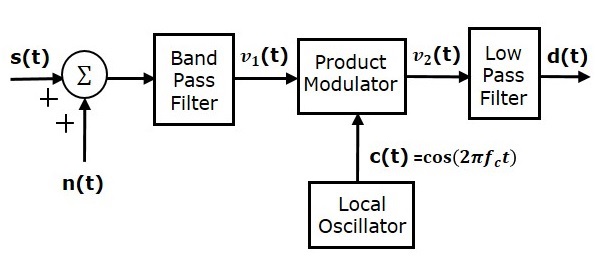
Sabemos que a onda modulada SSBSC com banda lateral inferior é
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
A potência média da onda modulada SSBSC é
$$ P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8} $$
A potência média de ruído na largura de banda da mensagem é
$$ P_ {nc} = WN_0 $$
Substitua, esses valores em channel SNR Fórmula.
$$ \ left (SNR \ right) _ {C, SSBSC} = \ frac {Média \: \: Potência \: \: de \: \: SSBSC \: \: modulado \: \: onda} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: mensagem \: \: largura de banda} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
Suponha que o ruído da passagem de banda seja misturado com a onda modulada SSBSC no canal, conforme mostrado na figura acima. Essa combinação é aplicada como uma das entradas para o modulador de produto. Portanto, a entrada deste modulador de produto é
$$ v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right) $$
$$ v_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] + n_I \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$
O oscilador local gera o sinal da portadora $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $. Este sinal é aplicado como outra entrada para o modulador do produto. Portanto, o modulador de produto produz uma saída, que é o produto de $ v_1 \ left (t \ right) $ e $ c \ left (t \ right) $.
$$ v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right) $$
Substitua os valores $ v_1 \ left (t \ right) $ e $ c \ left (t \ right) $ na equação acima.
$ \ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct) - $
$ n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ direita) + $
$ n_I \ left (t \ right) \ cos ^ 2 \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} + $
$ n_I \ left (t \ right) \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right) - n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2} $
Quando o sinal acima é aplicado como uma entrada para o filtro passa-baixo, obteremos a saída do filtro passa-baixo como
$$ d \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ right) + \ frac {n_I \ left (t \ right)} {2} $$
A potência média do sinal demodulado é
$$ P_m = \ left (\ frac {A_mA_c} {4 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} $$
A potência média de ruído na saída é
$$ P_ {no} = \ frac {WN_0} {4} $$
Substitua, esses valores em output SNR Fórmula
$$ \ left (SNR \ right) _ {O, SSBSC} = \ frac {Média \: \: Potência \: \: de \: \: demodulado \: \: sinal} {Média \: \: Potência \: \: de \: \: ruído \: \: em \: \: saída} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ right ) / \ left (\ frac {WN_0} {4} \ right) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
Substitua, os valores em Figure of merit da fórmula do receptor SSBSC
$$ F = \ frac {\ left (SNR \ right) _ {O, SSBSC}} {\ left (SNR \ right) _ {C, SSBSC}} $$
$$ F = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) / \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) $$
$$ F = 1 $$
Portanto, a Figura de mérito do receptor SSBSC é 1.