Comunicação Analógica - Modulação VSBSC
Nos capítulos anteriores, discutimos a modulação e demodulação SSBSC. O sinal modulado SSBSC tem apenas uma frequência de banda lateral. Teoricamente, podemos obter um componente de frequência de banda lateral completamente usando um filtro passa-banda ideal. No entanto, praticamente não podemos obter todo o componente de frequência da banda lateral. Devido a isso, algumas informações se perdem.
Para evitar essa perda, uma técnica é escolhida, que é um meio-termo entre DSBSC e SSBSC. Esta técnica é conhecida comoVestigial Side Band Suppressed Carrier (VSBSC)técnica. A palavra “vestígio” significa “uma parte” da qual o nome é derivado.
VSBSC Modulationé o processo em que uma parte do sinal denominado vestígio é modulada junto com uma faixa lateral. O espectro de frequência da onda VSBSC é mostrado na figura a seguir.

Junto com a banda lateral superior, uma parte da banda lateral inferior também está sendo transmitida nesta técnica. Da mesma forma, podemos transmitir a faixa lateral inferior junto com uma parte da faixa lateral superior. Uma faixa de proteção de largura muito pequena é colocada em cada lado do VSB para evitar as interferências. A modulação VSB é usada principalmente em transmissões de televisão.
Largura de banda da modulação VSBSC
Sabemos que a largura de banda da onda modulada SSBSC é $ f_m $. Visto que a onda modulada VSBSC contém os componentes de frequência de uma banda lateral junto com o vestígio da outra banda lateral, a largura de banda dela será a soma da largura de banda da onda modulada SSBSC e a frequência vestígio $ f_v $.
i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$
Vantagens
A seguir estão as vantagens da modulação VSBSC.
Altamente eficiente.
Redução da largura de banda quando comparada às ondas AM e DSBSC.
O projeto do filtro é fácil, pois não é necessária alta precisão.
A transmissão de componentes de baixa frequência é possível, sem qualquer dificuldade.
Possui boas características de fase.
Desvantagens
A seguir estão as desvantagens da modulação VSBSC.
A largura de banda é maior quando comparada à onda SSBSC.
A demodulação é complexa.
Formulários
A aplicação mais proeminente e padrão do VSBSC é para a transmissão de sinais de televisão. Além disso, essa é a técnica mais conveniente e eficiente quando o uso da largura de banda é considerado.
Agora, vamos discutir sobre o modulador que gera a onda VSBSC e o demodulador que demodula a onda VSBSC uma por uma.
Geração de VSBSC
A geração da onda VSBSC é semelhante à geração da onda SSBSC. O modulador VSBSC é mostrado na figura a seguir.
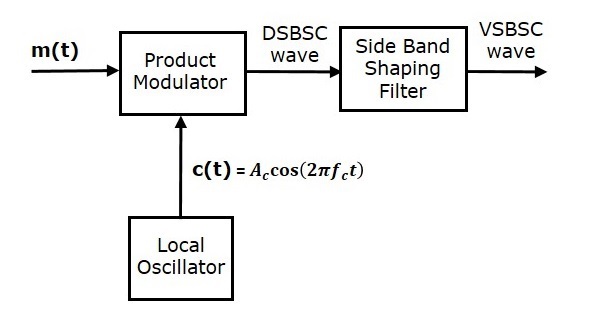
Neste método, primeiro iremos gerar a onda DSBSC com a ajuda do modulador do produto. Em seguida, aplique esta onda DSBSC como uma entrada do filtro de modelagem de banda lateral. Este filtro produz uma saída, que é onda VSBSC.
O sinal de modulação $ m \ left (t \ right) $ e o sinal da portadora $ A_c \ cos \ left (2 \ pi f_ct \ right) $ são aplicados como entradas para o modulador de produto. Portanto, o modulador de produto produz uma saída, que é o produto dessas duas entradas.
Portanto, a saída do modulador do produto é
$$ p \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$
Aplicar transformada de Fourier em ambos os lados
$$ P \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] $$
A equação acima representa a equação do espectro de frequência DSBSC.
Seja a função de transferência do filtro de modelagem da banda lateral $ H \ left (f \ right) $. Este filtro tem a entrada $ p \ left (t \ right) $ e a saída é a onda modulada VSBSC $ s \ left (t \ right) $. As transformadas de Fourier de $ p \ left (t \ right) $ e $ s \ left (t \ right) $ são $ P \ left (t \ right) $ e $ S \ left (t \ right) $ respectivamente.
Matematicamente, podemos escrever $ S \ left (f \ right) $ como
$$ S \ left (t \ right) = P \ left (f \ right) H \ left (f \ right) $$
Substitua o valor $ P \ left (f \ right) $ na equação acima.
$$ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ left ( f \ right) $$
A equação acima representa a equação do espectro de frequência VSBSC.
Demodulação de VSBSC
A demodulação da onda VSBSC é semelhante à demodulação da onda SSBSC. Aqui, o mesmo sinal de portadora (que é usado para gerar a onda VSBSC) é usado para detectar o sinal de mensagem. Portanto, este processo de detecção é chamado decoherent ou synchronous detection. O demodulador VSBSC é mostrado na figura a seguir.

Neste processo, o sinal de mensagem pode ser extraído da onda VSBSC, multiplicando-o por uma portadora, que está tendo a mesma frequência e fase da portadora utilizada na modulação VSBSC. O sinal resultante é então passado por um filtro passa-baixas. A saída desse filtro é o sinal de mensagem desejado.
Seja a onda VSBSC $ s \ left (t \ right) $ e o sinal da portadora é $ A_c \ cos \ left (2 \ pi f_ct \ right) $.
A partir da figura, podemos escrever a saída do modulador de produto como
$$ v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) s \ left (t \ right) $$
Aplicar transformada de Fourier em ambos os lados
$$ V \ left (f \ right) = \ frac {A_c} {2} \ left [S \ left (f-f_c \ right) + S \ left (f + f_c \ right) \ right] $$
Sabemos que $ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ esquerda (f \ direita) $
A partir da equação acima, vamos encontrar $ S \ left (f-f_c \ right) $ e $ S \ left (f + f_c \ right) $.
$$ S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c-f_c \ right) + M \ left (f-f_c + f_c \ right) \ direita] H \ esquerda (f-f_c \ direita) $$
$ \ Rightarrow S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-2f_c \ right) + M \ left (f \ right) \ right] H \ left (f-f_c \ right) $
$$ S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f + f_c-f_c \ right) + M \ left (f + f_c + f_c \ right) \ direita] H \ esquerda (f + f_c \ direita) $$
$ \ Rightarrow S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f \ right) + M \ left (f + 2f_c \ right) \ right] H \ left (f + f_c \ right) $
Substitua, $ S \ left (f-f_c \ right) $ e $ S \ left (f + f_c \ right) $ valores em $ V \ left (f \ right) $.
$ V (f) = \ frac {A_c} {2} [\ frac {A_c} {2} [M (f-2f_c) + M (f)] H (f-f_c) + $
$ \ frac {A_c} {2} [M (f) + M (f + 2f_c)] H (f + f_c)] $
$ \ Rightarrow V \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ esquerda (f + f_c \ direita) \ direita] $
$ + \ frac {{A_ {c}} ^ {2}} {4} \ left [M \ left (f-2f_c \ right) H \ left (f-f_c \ right) + M \ left (f + 2f_c \ direita) H \ esquerda (f + f_c \ direita) \ direita] $
Na equação acima, o primeiro termo representa a versão em escala do espectro de frequência do sinal de mensagem desejado. Ele pode ser extraído passando o sinal acima por um filtro passa-baixo.
$$ V_0 \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ left (f + f_c \ right) \ right] $$