Otimização convexa - mínimo e máximo
Mínimo local ou minimizar
$ \ bar {x} \ in \: S $ é considerado mínimo local de uma função $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ onde $ N_ \ varepsilon \ left (\ bar {x} \ right) $ significa vizinhança de $ \ bar {x} $, ou seja, $ N_ \ varejpsilon \ left (\ bar {x} \ right) $ significa $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $
Maxima local ou maximizador
$ \ bar {x} \ in \: S $ é considerado máximo local de uma função $ f $ if $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ onde $ N_ \ varepsilon \ left (\ bar {x} \ right) $ significa vizinhança de $ \ bar {x} $, ie, $ N_ \ varejpsilon \ left (\ bar {x} \ right) $ significa $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $
Mínimos globais
$ \ bar {x} \ in \: S $ são os mínimos globais de uma função $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in S $
Maxima global
$ \ bar {x} \ in \: S $ é considerado o máximo global de uma função $ f $ if $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in S $
Exemplos
Step 1- encontre os mínimos e máximos locais de $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ right | $
Solution -

A partir do gráfico da função acima, é claro que os mínimos locais ocorrem em $ x = \ pm 2 $ e os máximos locais em $ x = 0 $
Step 2- encontre os mínimos globais da função $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ right | $
Solution -
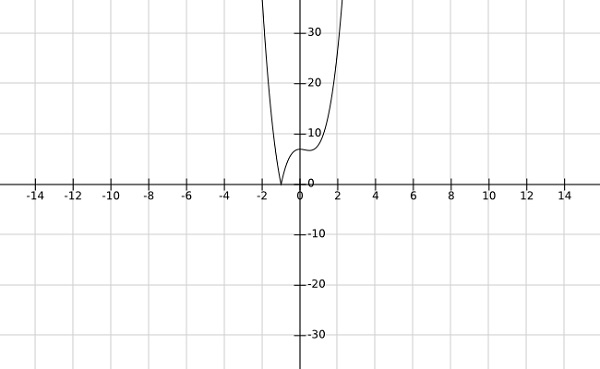
A partir do gráfico da função acima, é claro que os mínimos globais ocorrem em $ x = -1 $.