Circuitos Digitais - Máquinas de Estados Finitos
Sabemos que os circuitos sequenciais síncronos mudam (afetam) seus estados para cada transição positiva (ou negativa) do sinal de clock com base na entrada. Portanto, este comportamento de circuitos sequenciais síncronos pode ser representado na forma gráfica e é conhecido comostate diagram.
Um circuito sequencial síncrono também é chamado de Finite State Machine(FSM), se tiver número finito de estados. Existem dois tipos de FSMs.
- Mealy State Machine
- Moore State Machine
Agora, vamos discutir sobre essas duas máquinas de estado, uma por uma.
Mealy State Machine
Uma máquina de estados finitos é considerada uma máquina de estados de Mealy, se as saídas dependerem das entradas e dos estados presentes. oblock diagram da máquina de estado Mealy é mostrado na figura a seguir.
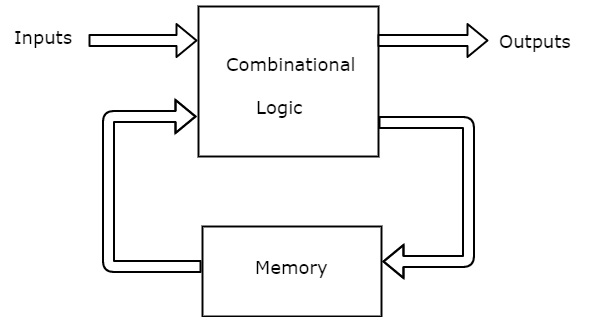
Conforme mostrado na figura, há duas partes presentes na máquina de estado de Mealy. Essas são lógica combinatória e memória. A memória é útil para fornecer algumas ou parte das saídas anteriores(present states) como entradas de lógica combinacional.
Portanto, com base nas entradas e nos estados presentes, a máquina de estados de Mealy produz saídas. Portanto, as saídas serão válidas apenas na transição positiva (ou negativa) do sinal de clock.
o state diagram da máquina de estado Mealy é mostrado na figura a seguir.
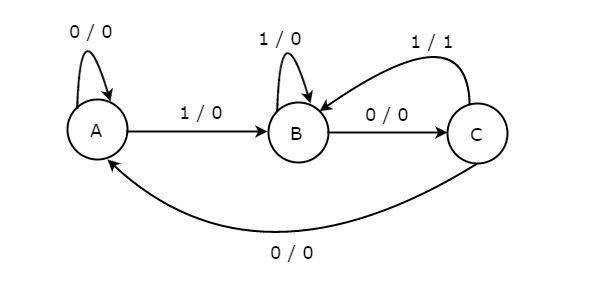
Na figura acima, existem três estados, a saber A, B e C. Esses estados são rotulados dentro dos círculos e cada círculo corresponde a um estado. As transições entre esses estados são representadas por linhas direcionadas. Aqui, 0/0, 1/0 e 1/1 denotainput / output. Na figura acima, existem duas transições de cada estado com base no valor da entrada, x.
Em geral, o número de estados exigidos na máquina de estados de Mealy é menor ou igual ao número de estados exigidos na máquina de estados de Moore. Há uma máquina de estado de Moore equivalente para cada máquina de estado de Mealy.
Moore State Machine
Uma máquina de estados finitos é considerada uma máquina de estados de Moore, se as saídas dependerem apenas dos estados presentes. oblock diagram da máquina de estado de Moore é mostrado na figura a seguir.

Conforme mostrado na figura, há duas partes presentes na máquina de estado de Moore. Essas são lógica combinatória e memória. Nesse caso, as entradas e os estados presentes determinam os próximos estados. Portanto, com base nos próximos estados, a máquina de estados de Moore produz as saídas. Portanto, as saídas serão válidas somente após a transição do estado.
o state diagram da máquina de estado de Moore é mostrado na figura a seguir.

Na figura acima, existem quatro estados, a saber, A, B, C e D. Esses estados e as respectivas saídas são rotulados dentro dos círculos. Aqui, apenas o valor de entrada é rotulado em cada transição. Na figura acima, existem duas transições de cada estado com base no valor da entrada, x.
Em geral, o número de estados necessários na máquina de estados de Moore é maior ou igual ao número de estados necessários na máquina de estados de Mealy. Há uma máquina de estado Mealy equivalente para cada máquina de estado de Moore. Portanto, com base no requisito, podemos usar um deles.