Circuitos digitais - Guia rápido
Se a base ou raiz de um sistema numérico for 'r', então os números presentes nesse sistema numérico variam de zero a r-1. O número total presente nesse sistema numérico é 'r'. Assim, obteremos vários sistemas numéricos, escolhendo os valores da raiz como maiores ou iguais a dois.
Neste capítulo, vamos discutir sobre o popular number systemse como representar um número no respectivo sistema numérico. Os seguintes sistemas numéricos são os mais comumente usados.
- Sistema de número decimal
- Sistema de número binário
- Sistema numérico octal
- Sistema numérico hexadecimal
Sistema de Número Decimal
o base ou a raiz do sistema de número decimal é 10. Portanto, os números que variam de 0 a 9 são usados neste sistema numérico. A parte do número que fica à esquerda dodecimal pointé conhecido como parte inteira. Da mesma forma, a parte do número à direita da vírgula decimal é conhecida como parte fracionária.
Neste sistema numérico, as posições sucessivas à esquerda da vírgula têm pesos de 10 0 , 10 1 , 10 2 , 10 3 e assim por diante. Da mesma forma, as posições sucessivas à direita do ponto decimal têm pesos de 10 -1 , 10 -2 , 10 -3 e assim por diante. Isso significa que cada posição tem peso específico, que épower of base 10
Exemplo
Considere o decimal number 1358.246. A parte inteira desse número é 1358 e a parte fracionária desse número é 0,246. Os dígitos 8, 5, 3 e 1 têm pesos de 100, 101, 10 2 e 10 3 respectivamente. Da mesma forma, os dígitos 2, 4 e 6 têm pesos de 10 -1 , 10 -2 e 10 -3, respectivamente.
Mathematically, podemos escrever como
1358,246 = (1 × 10 3 ) + (3 × 10 2 ) + (5 × 10 1 ) + (8 × 10 0 ) + (2 × 10 -1 ) +
(4 × 10 -2 ) + (6 × 10 -3 )
Depois de simplificar os termos do lado direito, obteremos o número decimal, que está do lado esquerdo.
Sistema de número binário
Todos os circuitos e sistemas digitais usam este sistema numérico binário. obase ou a raiz deste sistema numérico é 2. Portanto, os números 0 e 1 são usados neste sistema numérico.
A parte do número, que fica à esquerda do binary pointé conhecido como parte inteira. Da mesma forma, a parte do número que fica à direita do ponto binário é conhecida como parte fracionária.
Neste sistema numérico, as posições sucessivas à esquerda do ponto binário têm pesos de 2 0 , 2 1 , 2 2 , 2 3 e assim por diante. Da mesma forma, as posições sucessivas à direita do ponto binário têm pesos de 2 -1 , 2 -2 , 2 -3 e assim por diante. Isso significa que cada posição tem peso específico, que épower of base 2.
Exemplo
Considere o binary number 1101.011. A parte inteira desse número é 1101 e a parte fracionária desse número é 0,011. Os dígitos 1, 0, 1 e 1 da parte inteira têm pesos de 2 0 , 2 1 , 2 2 , 2 3 respectivamente. Da mesma forma, os dígitos 0, 1 e 1 da parte fracionária têm pesos de 2 -1 , 2 -2 , 2 -3 respectivamente.
Mathematically, podemos escrever como
1101,011 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (0 × 2 -1 ) +
(1 × 2 -2 ) + (1 × 2 -3 )
Depois de simplificar os termos do lado direito, obteremos um número decimal, que é equivalente ao número binário do lado esquerdo.
Octal Number System
o base ou a raiz do sistema numérico octal é 8. Portanto, os números que variam de 0 a 7 são usados neste sistema numérico. A parte do número que fica à esquerda dooctal pointé conhecido como parte inteira. Da mesma forma, a parte do número que está à direita do ponto octal é conhecida como parte fracionária.
Neste sistema numérico, as posições sucessivas à esquerda do ponto octal têm pesos de 8 0 , 8 1 , 8 2 , 8 3 e assim por diante. Da mesma forma, as posições sucessivas à direita do ponto octal têm pesos de 8 -1 , 8 -2 , 8 -3 e assim por diante. Isso significa que cada posição tem peso específico, que épower of base 8.
Exemplo
Considere o octal number 1457.236. A parte inteira desse número é 1457 e a parte fracionária desse número é 0,236. Os dígitos 7, 5, 4 e 1 têm pesos de 8 0 , 8 1 , 8 2 e 8 3 respectivamente. Da mesma forma, os dígitos 2, 3 e 6 têm pesos de 8 -1 , 8 -2 , 8 -3, respectivamente.
Mathematically, podemos escrever como
1457,236 = (1 × 8 3 ) + (4 × 8 2 ) + (5 × 8 1 ) + (7 × 8 0 ) + (2 × 8 -1 ) +
(3 × 8 -2 ) + (6 × 8 -3 )
Depois de simplificar os termos do lado direito, obteremos um número decimal, que é equivalente ao número octal do lado esquerdo.
Sistema numérico hexadecimal
o base ou a raiz do sistema numérico hexa-decimal é 16. Portanto, os números que variam de 0 a 9 e as letras de A a F são usados neste sistema numérico. O equivalente decimal de dígitos hexa-decimais de A a F são de 10 a 15.
A parte do número, que fica à esquerda do hexadecimal pointé conhecido como parte inteira. Da mesma forma, a parte do número, que fica à direita do ponto decimal hexa, é conhecida como parte fracionária.
Neste sistema numérico, as posições sucessivas à esquerda da vírgula hexa-decimal têm pesos de 16 0 , 16 1 , 16 2 , 16 3 e assim por diante. Da mesma forma, as posições sucessivas à direita do ponto hexa-decimal têm pesos de 16 -1 , 16 -2 , 16 -3 e assim por diante. Isso significa que cada posição tem peso específico, que épower of base 16.
Exemplo
Considere o Hexa-decimal number 1A05.2C4. A parte inteira desse número é 1A05 e a parte fracionária desse número é 0,2C4. Os dígitos 5, 0, A e 1 têm pesos de 16 0 , 16 1 , 16 2 e 16 3 respectivamente. Da mesma forma, os dígitos 2, C e 4 têm pesos de 16 -1 , 16 -2 e 16 -3, respectivamente.
Mathematically, podemos escrever como
1A05.2C4 = (1 × 16 3 ) + (10 × 16 2 ) + (0 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 ) +
(12 × 16 -2 ) + (4 × 16 -3 )
Depois de simplificar os termos do lado direito, obteremos um número decimal, que é equivalente ao número hexa-decimal do lado esquerdo.
No capítulo anterior, vimos os quatro sistemas numéricos proeminentes. Neste capítulo, vamos converter os números de um sistema numérico para o outro para encontrar o valor equivalente.
Conversão de número decimal para outras bases
Se o número decimal contiver parte inteira e parte fracionária, converta ambas as partes do número decimal em outra base individualmente. Siga estas etapas para converter o número decimal em seu número equivalente de qualquer base 'r'.
Faz division da parte inteira do número decimal e successive quotientscom base 'r' e anote os restos até que o quociente seja zero. Considere os restos em ordem reversa para obter a parte inteira do número equivalente da base 'r'. Isso significa que o primeiro e o último resto denotam o dígito menos significativo e o dígito mais significativo, respectivamente.
Faz multiplication da parte fracionária do número decimal e successive fractionscom a base 'r' e anote o transporte até que o resultado seja zero ou o número desejado de dígitos equivalentes seja obtido. Considere a sequência normal de transporte para obter a parte fracionária do número equivalente de base 'r'.
Conversão decimal para binário
Os dois tipos de operação a seguir ocorrem durante a conversão do número decimal em seu número binário equivalente.
- Divisão de parte inteira e quocientes sucessivos com base 2.
- Multiplicação da parte fracionária e frações sucessivas com base 2.
Example
Considere o decimal number 58.25. Aqui, a parte inteira é 58 e a parte fracionária é 0,25.
Step 1 - Divisão de 58 e quocientes sucessivos com base 2.
| Operação | Quociente | Restante |
|---|---|---|
| 58/2 | 29 | 0 (LSB) |
| 29/2 | 14 | 1 |
| 14/2 | 7 | 0 |
| 7/2 | 3 | 1 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1(MSB) |
⇒ (58) 10 = (111010) 2
Portanto, o integer part de número binário equivalente é 111010.
Step 2 - Multiplicação de 0,25 e frações sucessivas com base 2.
| Operação | Resultado | Carregar |
|---|---|---|
| 0,25 x 2 | 0,5 | 0 |
| 0,5 x 2 | 1.0 | 1 |
| - | 0,0 | - |
⇒ (0,25) 10 = (0,01) 2
Portanto, o fractional part de número binário equivalente é .01
⇒ (58,25) 10 = (111010,01) 2
Portanto, o binary equivalent do número decimal 58,25 é 111010,01.
Conversão Decimal para Octal
Os dois tipos de operação a seguir ocorrem durante a conversão do número decimal em seu número octal equivalente.
Divisão de parte inteira e quocientes sucessivos com base 8.
Multiplicação da parte fracionária e frações sucessivas com base 8.
Example
Considere o decimal number 58.25. Aqui, a parte inteira é 58 e a parte fracionária é 0,25.
Step 1 - Divisão de 58 e quocientes sucessivos com base 8.
| Operação | Quociente | Restante |
|---|---|---|
| 58/8 | 7 | 2 |
| 7/8 | 0 | 7 |
⇒ (58) 10 = (72) 8
Portanto, o integer part de número octal equivalente é 72.
Step 2 - Multiplicação de 0,25 e frações sucessivas com base 8.
| Operação | Resultado | Carregar |
|---|---|---|
| 0,25 x 8 | 2,00 | 2 |
| - | 0,00 | - |
⇒ (0,25) 10 = (0,2) 8
Portanto, o fractional part do número octal equivalente é .2
⇒ (58,25) 10 = (72,2) 8
Portanto, o octal equivalent do número decimal 58,25 é 72,2.
Conversão Decimal para Hexa-Decimal
Os dois tipos de operações a seguir ocorrem durante a conversão do número decimal em seu número hexa-decimal equivalente.
- Divisão de parte inteira e quocientes sucessivos com base 16.
- Multiplicação da parte fracionária e frações sucessivas com base 16.
Example
Considere o decimal number 58.25. Aqui, a parte inteira é 58 e a parte decimal é 0,25.
Step 1 - Divisão de 58 e quocientes sucessivos com base 16.
| Operação | Quociente | Restante |
|---|---|---|
| 58/16 | 3 | 10 = A |
| 3/16 | 0 | 3 |
⇒ (58) 10 = (3A) 16
Portanto, o integer part de número hexa-decimal equivalente é 3A.
Step 2 - Multiplicação de 0,25 e frações sucessivas com base 16.
| Operação | Resultado | Carregar |
|---|---|---|
| 0,25 x 16 | 4,00 | 4 |
| - | 0,00 | - |
⇒ (0,25) 10 = (0,4) 16
Portanto, o fractional part do número hexa-decimal equivalente é 0,4.
⇒(58.25)10 = (3A.4)16
Portanto, o Hexa-decimal equivalent do número decimal 58,25 é 3A.4.
Conversão de número binário para outras bases
O processo de conversão de um número binário em decimal é diferente do processo de conversão de um número binário em outras bases. Agora, vamos discutir sobre a conversão de um número binário em sistemas numéricos decimais, octais e hexadecimais, um por um.
Conversão de binário para decimal
Para converter um número binário em seu número decimal equivalente, primeiro multiplique os bits do número binário pelos respectivos pesos posicionais e, em seguida, some todos esses produtos.
Example
Considere o binary number 1101.11.
Mathematically, podemos escrever como
(1101.11) 2 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (1 × 2 -1 ) +
(1 × 2 -2 )
⇒ (1101,11) 2 = 8 + 4 + 0 + 1 + 0,5 + 0,25 = 13,75
⇒ (1101,11) 2 = (13,75) 10
Portanto, o decimal equivalent do número binário 1101,11 é 13,75.
Conversão de binário para octal
Sabemos que as bases dos sistemas numéricos binários e octais são 2 e 8, respectivamente. Três bits de número binário são equivalentes a um dígito octal, já que 2 3 = 8.
Siga estas duas etapas para converter um número binário em seu número octal equivalente.
Comece do ponto binário e faça os grupos de 3 bits em ambos os lados do ponto binário. Se um ou dois bits forem menores ao formar o grupo de 3 bits, inclua o número necessário de zeros nos lados extremos.
Escreva os dígitos octais correspondentes a cada grupo de 3 bits.
Example
Considere o binary number 101110.01101.
Step 1 - Faça os grupos de 3 bits em ambos os lados do ponto binário.
101 110.011 01
Aqui, do lado direito do ponto binário, o último grupo tem apenas 2 bits. Portanto, inclua um zero no lado extremo para torná-lo um grupo de 3 bits.
⇒ 101 110,011 010
Step 2 - Escreva os dígitos octais correspondentes a cada grupo de 3 bits.
⇒ (101 110,011 010) 2 = (56,32) 8
Portanto, o octal equivalent do número binário 101110.01101 é 56,32.
Conversão de binário para hexa-decimal
Sabemos que as bases dos sistemas numéricos binários e hexa-decimais são 2 e 16, respectivamente. Quatro bits de número binário são equivalentes a um dígito hexa-decimal, uma vez que 2 4 = 16.
Siga estas duas etapas para converter um número binário em seu número hexa-decimal equivalente.
Comece do ponto binário e faça os grupos de 4 bits em ambos os lados do ponto binário. Se alguns bits forem menores ao formar o grupo de 4 bits, inclua o número necessário de zeros nos lados extremos.
Escreva os dígitos hexa-decimais correspondentes a cada grupo de 4 bits.
Example
Considere o binary number 101110.01101
Step 1 - Faça os grupos de 4 bits em ambos os lados do ponto binário.
10 1110.0110 1
Aqui, o primeiro grupo tem apenas 2 bits. Portanto, inclua dois zeros no lado extremo para torná-lo um grupo de 4 bits. Da mesma forma, inclua três zeros no lado extremo para fazer o último grupo também como um grupo de 4 bits.
⇒ 0010 1110.0110 1000
Step 2 - Escreva os dígitos hexa-decimais correspondentes a cada grupo de 4 bits.
⇒ (0010 1110,0110 1000) 2 = (2E.68) 16
Portanto, o Hexa-decimal equivalent do número binário 101110.01101 é (2E.68).
Conversão de número octal para outras bases
O processo de conversão de um número octal em decimal é diferente do processo de conversão de um número octal em outras bases. Agora, vamos discutir sobre a conversão de um número octal em sistemas numéricos decimais, binários e hexadecimais, um por um.
Conversão de Octal para Decimal
Para converter um número octal em seu número decimal equivalente, primeiro multiplique os dígitos do número octal pelos respectivos pesos posicionais e, em seguida, some todos esses produtos.
Example
Considere o octal number 145.23.
Mathematically, podemos escrever como
(145,23) 8 = (1 × 8 2 ) + (4 × 8 1 ) + (5 × 8 0 ) + (2 × 8 -1 ) + (3 × 8 -2 )
⇒ (145,23) 8 = 64 + 32 + 5 + 0,25 + 0,05 = 101,3
⇒ (145,23) 8 = (101,3) 10
Portanto, o decimal equivalent do número octal 145,23 é 101,3.
Conversão de octal para binário
O processo de conversão de um número octal em um número binário equivalente é exatamente oposto ao da conversão de binário em octal. Ao representar cada dígito octal com 3 bits, obteremos o número binário equivalente.
Example
Considere o octal number 145.23.
Represente cada dígito octal com 3 bits.
(145,23) 8 = (001 100 101,010 011) 2
O valor não muda removendo os zeros, que estão no lado extremo.
⇒ (145,23) 8 = (1100101.010011) 2
Portanto, o binary equivalent do número octal 145,23 é 1100101.010011.
Conversão de octal para hexa-decimal
Siga estas duas etapas para converter um número octal em seu número hexa-decimal equivalente.
- Converta o número octal em seu número binário equivalente.
- Converta o número binário acima em seu número hexadecimal equivalente.
Example
Considere o octal number 145.23
No exemplo anterior, obtivemos o equivalente binário do número octal 145,23 como 1100101.010011.
Seguindo o procedimento de conversão binária para hexadecimal, obteremos
(1100101.010011) 2 = (65.4C) 16
⇒ (145,23) 8 = (65,4C) 16
Portanto, o Hexa-decimal equivalentde número octal 145,23 é 65,4 C .
Conversão de número hexa-decimal para outras bases
O processo de conversão de um número hexadecimal em decimal é diferente do processo de conversão de um número hexadecimal em outras bases. Agora, vamos discutir sobre a conversão de números hexa-decimais em sistemas numéricos decimais, binários e octais, um por um.
Conversão hexa-decimal em decimal
Para converter o número hexa-decimal em seu número decimal equivalente, primeiro multiplique os dígitos do número hexa-decimal pelos respectivos pesos posicionais e, em seguida, some todos esses produtos.
Example
Considere o Hexa-decimal number 1A5.2
Mathematically, podemos escrever como
(1A5.2) 16 = (1 × 16 2 ) + (10 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 )
⇒ (1A5.2) 16 = 256 + 160 + 5 + 0,125 = 421,125
⇒ (1A5.2) 16 = (421.125) 10
Portanto, o decimal equivalent do número hexa-decimal 1A5.2 é 421.125.
Conversão hexa-decimal para binário
O processo de conversão de um número hexa-decimal em seu número binário equivalente é exatamente o oposto daquele da conversão de binário em hexa-decimal. Ao representar cada dígito hexa-decimal com 4 bits, obteremos o número binário equivalente.
Example
Considere o Hexa-decimal number 65.4C
Representa cada dígito hexa-decimal com 4 bits.
(65,4C) 6 = (0110 0101,0100 1100) 2
O valor não muda removendo os zeros, que estão em dois lados extremos.
⇒ (65.4C) 16 = (1100101.010011) 2
Portanto, o binary equivalent do número hexa-decimal 65.4C é 1100101.010011.
Conversão hexa-decimal para octal
Siga estas duas etapas para converter o número hexa-decimal em seu número octal equivalente.
- Converta o número hexa-decimal em seu número binário equivalente.
- Converta o número binário acima em seu número octal equivalente.
Example
Considere o Hexa-decimal number 65.4C
No exemplo anterior, obtivemos o equivalente binário do número hexa-decimal 65.4C como 1100101.010011.
Seguindo o procedimento de conversão binária em octal, obteremos
(1100101.010011) 2 = (145,23) 8
⇒ (65,4C) 16 = (145,23)
Portanto, o octal equivalentdo número hexa -decimal 65,4 C é 145,23.
Podemos transformar os números binários nos dois grupos a seguir - Unsigned numbers e Signed numbers.
Números sem sinal
Os números sem sinal contêm apenas a magnitude do número. Eles não têm nenhum sinal. Isso significa que todos os números binários sem sinal são positivos. Como no sistema de numeração decimal, a colocação de um sinal positivo antes do número é opcional para representar números positivos. Portanto, todos os números positivos, incluindo zero, podem ser tratados como números sem sinal se o sinal positivo não for atribuído na frente do número.
Números Assinados
Os números assinados contêm o sinal e a magnitude do número. Geralmente, o sinal é colocado na frente do número. Portanto, temos que considerar o sinal positivo para números positivos e o sinal negativo para números negativos. Portanto, todos os números podem ser tratados como números com sinais se o sinal correspondente for atribuído na frente do número.
Se o bit de sinal for zero, o que indica que o número binário é positivo. Da mesma forma, se o bit de sinal for um, o que indica que o número binário é negativo.
Representação de números binários não assinados
Os bits presentes no número binário não assinado contém o magnitudede um número. Isso significa que se o número binário não assinado contém‘N’ bits, então todos N os bits representam a magnitude do número, uma vez que não possui nenhum bit de sinal.
Example
Considere o decimal number 108. O equivalente binário deste número é1101100. Esta é a representação do número binário sem sinal.
(108) 10 = (1101100) 2
Está tendo 7 bits. Esses 7 bits representam a magnitude do número 108.
Representação de números binários assinados
O bit mais significativo (MSB) dos números binários com sinal é usado para indicar o sinal dos números. Portanto, também é chamado design bit. O sinal positivo é representado colocando '0' no bit de sinal. Da mesma forma, o sinal negativo é representado colocando '1' no bit de sinal.
Se o número binário com sinal contém 'N' bits, então (N-1) bits representam apenas a magnitude do número, uma vez que um bit (MSB) é reservado para representar o sinal do número.
Há três types of representations para números binários assinados
- Formulário Sign-Magnitude
- Forma de complemento de 1
- Forma de complemento de 2
A representação de um número positivo em todas essas 3 formas é a mesma. Mas, apenas a representação do número negativo será diferente em cada forma.
Example
Considere o positive decimal number +108. O equivalente binário de magnitude desse número é 1101100. Esses 7 bits representam a magnitude do número 108. Como é um número positivo, considere o bit de sinal como zero, que é colocado no lado esquerdo da magnitude.
(+108) 10 = (01101100) 2
Portanto, o signed binary representationde número decimal positivo +108 é. Portanto, a mesma representação é válida na forma de sinal-magnitude, forma de complemento de 1 e forma de complemento de 2 para número decimal positivo +108.
Formulário Sign-Magnitude
Na forma de magnitude de sinal, o MSB é usado para representar sign do número e os bits restantes representam o magnitudedo número. Portanto, apenas inclua o bit de sinal no lado esquerdo do número binário sem sinal. Esta representação é semelhante à representação de números decimais com sinal.
Example
Considere o negative decimal number -108. A magnitude desse número é 108. Sabemos que a representação binária sem sinal de 108 é 1101100. Ele tem 7 bits. Todos esses bits representam a magnitude.
Como o número fornecido é negativo, considere o bit de sinal como um, que é colocado no lado esquerdo da magnitude.
(−108) 10 = (11101100) 2
Portanto, a representação da magnitude do sinal de -108 é 11101100.
Forma de complemento de 1
O complemento de 1 de um número é obtido por complementing all the bitsde número binário assinado. Portanto, o complemento de 1 de número positivo dá um número negativo. Da mesma forma, o complemento de 1 de número negativo fornece um número positivo.
Isso significa que, se você executar duas vezes o complemento de 1 de um número binário incluindo o bit de sinal, obterá o número binário assinado original.
Example
Considere o negative decimal number -108. A magnitude desse número é 108. Sabemos que a representação binária com sinal de 108 é 01101100.
Está tendo 8 bits. O MSB deste número é zero, o que indica um número positivo. Complemento de zero é um e vice-versa. Portanto, substitua zeros por uns e uns por zeros para obter o número negativo.
(−108) 10 = (10010011) 2
Portanto, o 1’s complement of (108)10 é (10010011)2.
Forma de complemento de 2
O complemento de 2 de um número binário é obtido por adding one to the 1’s complementde número binário assinado. Portanto, o complemento de 2 do número positivo dá um número negativo. Da mesma forma, o complemento de 2 do número negativo fornece um número positivo.
Isso significa que, se você executar duas vezes o complemento de 2 de um número binário incluindo o bit de sinal, obterá o número binário com sinal original.
Example
Considere o negative decimal number -108.
Conhecemos o complemento de 1 de (108)10 é (10010011)2
Elogio de 2 de (108) 10 = elogio de 1 de (108) 10 + 1.
= 10010011 + 1
= 10010100
Portanto, o 2’s complement of (108)10 é (10010100)2.
Neste capítulo, vamos discutir sobre as operações aritméticas básicas, que podem ser realizadas em quaisquer dois números binários com sinal usando o método do complemento de 2. obasic arithmetic operations são adição e subtração.
Adição de dois números binários assinados
Considere os dois números binários com sinal A e B, que são representados na forma de complemento de 2. Podemos realizar oadditiondesses dois números, o que é semelhante à adição de dois números binários sem sinal. Mas, se a soma resultante contém carry out do bit de sinal, então descarte (ignore) para obter o valor correto.
Se a soma resultante for positiva, você pode encontrar a magnitude dela diretamente. Mas, se a soma resultante for negativa, então pegue o complemento de 2 dela para obter a magnitude.
Exemplo 1
Vamos realizar o addition de dois números decimais +7 and +4 usando o método do complemento de 2.
o 2’s complement representações de +7 e +4 com 5 bits cada são mostradas abaixo.
(+7) 10 = (00111) 2
(+4) 10 = (00100) 2
A adição desses dois números é
(+7) 10 + (+ 4) 10 = (00111) 2 + (00100) 2
⇒ (+7) 10 + (+ 4) 10 = (01011) 2 .
A soma resultante contém 5 bits. Portanto, não há execução do bit de sinal. O bit de sinal '0' indica que a soma resultante épositive. Portanto, a magnitude da soma é 11 no sistema numérico decimal. Portanto, a adição de dois números positivos dará outro número positivo.
Exemplo 2
Vamos realizar o addition de dois números decimais -7 e -4 usando o método do complemento de 2.
o 2’s complement representação de -7 e -4 com 5 bits cada são mostrados abaixo.
(−7) 10 = (11001) 2
(−4) 10 = (11100) 2
A adição desses dois números é
(−7) 10 + (−4) 10 = (11001) 2 + (11100) 2
⇒(−7)10 + (−4)10 = (110101)2.
The resultant sum contains 6 bits. In this case, carry is obtained from sign bit. So, we can remove it
Resultant sum after removing carry is (−7)10 + (−4)10 = (10101)2.
The sign bit ‘1’ indicates that the resultant sum is negative. So, by taking 2’s complement of it we will get the magnitude of resultant sum as 11 in decimal number system. Therefore, addition of two negative numbers will give another negative number.
Subtraction of two Signed Binary Numbers
Consider the two signed binary numbers A & B, which are represented in 2’s complement form. We know that 2’s complement of positive number gives a negative number. So, whenever we have to subtract a number B from number A, then take 2’s complement of B and add it to A. So, mathematically we can write it as
A - B = A + (2's complement of B)
Similarly, if we have to subtract the number A from number B, then take 2’s complement of A and add it to B. So, mathematically we can write it as
B - A = B + (2's complement of A)
So, the subtraction of two signed binary numbers is similar to the addition of two signed binary numbers. But, we have to take 2’s complement of the number, which is supposed to be subtracted. This is the advantage of 2’s complement technique. Follow, the same rules of addition of two signed binary numbers.
Example 3
Let us perform the subtraction of two decimal numbers +7 and +4 using 2’s complement method.
The subtraction of these two numbers is
(+7)10 − (+4)10 = (+7)10 + (−4)10.
The 2’s complement representation of +7 and -4 with 5 bits each are shown below.
(+7)10 = (00111)2
(+4)10 = (11100)2
⇒(+7)10 + (+4)10 = (00111)2 + (11100)2 = (00011)2
Here, the carry obtained from sign bit. So, we can remove it. The resultant sum after removing carry is
(+7)10 + (+4)10 = (00011)2
The sign bit ‘0’ indicates that the resultant sum is positive. So, the magnitude of it is 3 in decimal number system. Therefore, subtraction of two decimal numbers +7 and +4 is +3.
Example 4
Let us perform the subtraction of two decimal numbers +4 and +7 using 2’s complement method.
The subtraction of these two numbers is
(+4)10 − (+7)10 = (+4)10 + (−7)10.
The 2’s complement representation of +4 and -7 with 5 bits each are shown below.
(+4)10 = (00100)2
(-7)10 = (11001)2
⇒(+4)10 + (-7)10 = (00100)2 + (11001)2 = (11101)2
Here, carry is not obtained from sign bit. The sign bit ‘1’ indicates that the resultant sum is negative. So, by taking 2’s complement of it we will get the magnitude of resultant sum as 3 in decimal number system. Therefore, subtraction of two decimal numbers +4 and +7 is -3.
In the coding, when numbers or letters are represented by a specific group of symbols, it is said to be that number or letter is being encoded. The group of symbols is called as code. The digital data is represented, stored and transmitted as group of bits. This group of bits is also called as binary code.
Binary codes can be classified into two types.
- Weighted codes
- Unweighted codes
If the code has positional weights, then it is said to be weighted code. Otherwise, it is an unweighted code. Weighted codes can be further classified as positively weighted codes and negatively weighted codes.
Binary Codes for Decimal digits
The following table shows the various binary codes for decimal digits 0 to 9.
| Decimal Digit | 8421 Code | 2421 Code | 84-2-1 Code | Excess 3 Code |
|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 |
| 1 | 0001 | 0001 | 0111 | 0100 |
| 2 | 0010 | 0010 | 0110 | 0101 |
| 3 | 0011 | 0011 | 0101 | 0110 |
| 4 | 0100 | 0100 | 0100 | 0111 |
| 5 | 0101 | 1011 | 1011 | 1000 |
| 6 | 0110 | 1100 | 1010 | 1001 |
| 7 | 0111 | 1101 | 1001 | 1010 |
| 8 | 1000 | 1110 | 1000 | 1011 |
| 9 | 1001 | 1111 | 1111 | 1100 |
We have 10 digits in decimal number system. To represent these 10 digits in binary, we require minimum of 4 bits. But, with 4 bits there will be 16 unique combinations of zeros and ones. Since, we have only 10 decimal digits, the other 6 combinations of zeros and ones are not required.
8 4 2 1 code
The weights of this code are 8, 4, 2 and 1.
This code has all positive weights. So, it is a positively weighted code.
This code is also called as natural BCD (Binary Coded Decimal) code.
Example
Let us find the BCD equivalent of the decimal number 786. This number has 3 decimal digits 7, 8 and 6. From the table, we can write the BCD (8421) codes of 7, 8 and 6 are 0111, 1000 and 0110 respectively.
∴ (786)10 = (011110000110)BCD
There are 12 bits in BCD representation, since each BCD code of decimal digit has 4 bits.
2 4 2 1 code
The weights of this code are 2, 4, 2 and 1.
This code has all positive weights. So, it is a positively weighted code.
It is an unnatural BCD code. Sum of weights of unnatural BCD codes is equal to 9.
It is a self-complementing code. Self-complementing codes provide the 9’s complement of a decimal number, just by interchanging 1’s and 0’s in its equivalent 2421 representation.
Example
Let us find the 2421 equivalent of the decimal number 786. This number has 3 decimal digits 7, 8 and 6. From the table, we can write the 2421 codes of 7, 8 and 6 are 1101, 1110 and 1100 respectively.
Therefore, the 2421 equivalent of the decimal number 786 is 110111101100.
8 4 -2 -1 code
The weights of this code are 8, 4, -2 and -1.
This code has negative weights along with positive weights. So, it is a negatively weighted code.
It is an unnatural BCD code.
It is a self-complementing code.
Example
Let us find the 8 4-2-1 equivalent of the decimal number 786. This number has 3 decimal digits 7, 8 and 6. From the table, we can write the 8 4 -2 -1 codes of 7, 8 and 6 are 1001, 1000 and 1010 respectively.
Therefore, the 8 4 -2 -1 equivalent of the decimal number 786 is 100110001010.
Excess 3 code
This code doesn’t have any weights. So, it is an un-weighted code.
We will get the Excess 3 code of a decimal number by adding three (0011) to the binary equivalent of that decimal number. Hence, it is called as Excess 3 code.
It is a self-complementing code.
Example
Let us find the Excess 3 equivalent of the decimal number 786. This number has 3 decimal digits 7, 8 and 6. From the table, we can write the Excess 3 codes of 7, 8 and 6 are 1010, 1011 and 1001 respectively.
Therefore, the Excess 3 equivalent of the decimal number 786 is 101010111001
Gray Code
The following table shows the 4-bit Gray codes corresponding to each 4-bit binary code.
| Decimal Number | Binary Code | Gray Code |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
This code doesn’t have any weights. So, it is an un-weighted code.
In the above table, the successive Gray codes are differed in one bit position only. Hence, this code is called as unit distance code.
Binary code to Gray Code Conversion
Follow these steps for converting a binary code into its equivalent Gray code.
Consider the given binary code and place a zero to the left of MSB.
Compare the successive two bits starting from zero. If the 2 bits are same, then the output is zero. Otherwise, output is one.
Repeat the above step till the LSB of Gray code is obtained.
Example
From the table, we know that the Gray code corresponding to binary code 1000 is 1100. Now, let us verify it by using the above procedure.
Given, binary code is 1000.
Step 1 − By placing zero to the left of MSB, the binary code will be 01000.
Step 2 − By comparing successive two bits of new binary code, we will get the gray code as 1100.
We know that the bits 0 and 1 corresponding to two different range of analog voltages. So, during transmission of binary data from one system to the other, the noise may also be added. Due to this, there may be errors in the received data at other system.
That means a bit 0 may change to 1 or a bit 1 may change to 0. We can’t avoid the interference of noise. But, we can get back the original data first by detecting whether any error(s) present and then correcting those errors. For this purpose, we can use the following codes.
- Error detection codes
- Error correction codes
Error detection codes − are used to detect the error(s) present in the received data (bit stream). These codes contain some bit(s), which are included (appended) to the original bit stream. These codes detect the error, if it is occurred during transmission of the original data (bit stream).Example − Parity code, Hamming code.
Error correction codes − are used to correct the error(s) present in the received data (bit stream) so that, we will get the original data. Error correction codes also use the similar strategy of error detection codes.Example − Hamming code.
Therefore, to detect and correct the errors, additional bit(s) are appended to the data bits at the time of transmission.
Parity Code
It is easy to include (append) one parity bit either to the left of MSB or to the right of LSB of original bit stream. There are two types of parity codes, namely even parity code and odd parity code based on the type of parity being chosen.
Even Parity Code
The value of even parity bit should be zero, if even number of ones present in the binary code. Otherwise, it should be one. So that, even number of ones present in even parity code. Even parity code contains the data bits and even parity bit.
The following table shows the even parity codes corresponding to each 3-bit binary code. Here, the even parity bit is included to the right of LSB of binary code.
| Binary Code | Even Parity bit | Even Parity Code |
|---|---|---|
| 000 | 0 | 0000 |
| 001 | 1 | 0011 |
| 010 | 1 | 0101 |
| 011 | 0 | 0110 |
| 100 | 1 | 1001 |
| 101 | 0 | 1010 |
| 110 | 0 | 1100 |
| 111 | 1 | 1111 |
Here, the number of bits present in the even parity codes is 4. So, the possible even number of ones in these even parity codes are 0, 2 & 4.
If the other system receives one of these even parity codes, then there is no error in the received data. The bits other than even parity bit are same as that of binary code.
If the other system receives other than even parity codes, then there will be an error(s) in the received data. In this case, we can’t predict the original binary code because we don’t know the bit position(s) of error.
Therefore, even parity bit is useful only for detection of error in the received parity code. But, it is not sufficient to correct the error.
Odd Parity Code
The value of odd parity bit should be zero, if odd number of ones present in the binary code. Otherwise, it should be one. So that, odd number of ones present in odd parity code. Odd parity code contains the data bits and odd parity bit.
The following table shows the odd parity codes corresponding to each 3-bit binary code. Here, the odd parity bit is included to the right of LSB of binary code.
| Binary Code | Odd Parity bit | Odd Parity Code |
|---|---|---|
| 000 | 1 | 0001 |
| 001 | 0 | 0010 |
| 010 | 0 | 0100 |
| 011 | 1 | 0111 |
| 100 | 0 | 1000 |
| 101 | 1 | 1011 |
| 110 | 1 | 1101 |
| 111 | 0 | 1110 |
Here, the number of bits present in the odd parity codes is 4. So, the possible odd number of ones in these odd parity codes are 1 & 3.
If the other system receives one of these odd parity codes, then there is no error in the received data. The bits other than odd parity bit are same as that of binary code.
If the other system receives other than odd parity codes, then there is an error(s) in the received data. In this case, we can’t predict the original binary code because we don’t know the bit position(s) of error.
Therefore, odd parity bit is useful only for detection of error in the received parity code. But, it is not sufficient to correct the error.
Hamming Code
Hamming code is useful for both detection and correction of error present in the received data. This code uses multiple parity bits and we have to place these parity bits in the positions of powers of 2.
The minimum value of 'k' for which the following relation is correct (valid) is nothing but the required number of parity bits.
$$2^k\geq n+k+1$$
Where,
‘n’ is the number of bits in the binary code (information)
‘k’ is the number of parity bits
Therefore, the number of bits in the Hamming code is equal to n + k.
Let the Hamming code is $b_{n+k}b_{n+k-1}.....b_{3}b_{2}b_{1}$ & parity bits $p_{k}, p_{k-1}, ....p_{1}$. We can place the ‘k’ parity bits in powers of 2 positions only. In remaining bit positions, we can place the ‘n’ bits of binary code.
Based on requirement, we can use either even parity or odd parity while forming a Hamming code. But, the same parity technique should be used in order to find whether any error present in the received data.
Follow this procedure for finding parity bits.
Find the value of p1, based on the number of ones present in bit positions b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of p2, based on the number of ones present in bit positions b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of p3, based on the number of ones present in bit positions b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of parity bits.
Follow this procedure for finding check bits.
Find the value of c1, based on the number of ones present in bit positions b1, b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of c2, based on the number of ones present in bit positions b2, b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of c3, based on the number of ones present in bit positions b4, b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of check bits.
The decimal equivalent of the check bits in the received data gives the value of bit position, where the error is present. Just complement the value present in that bit position. Therefore, we will get the original binary code after removing parity bits.
Example 1
Let us find the Hamming code for binary code, d4d3d2d1 = 1000. Consider even parity bits.
The number of bits in the given binary code is n=4.
We can find the required number of parity bits by using the following mathematical relation.
$$2^k\geq n+k+1$$
Substitute, n=4 in the above mathematical relation.
$$\Rightarrow 2^k\geq 4+k+1$$
$$\Rightarrow 2^k\geq 5+k$$
The minimum value of k that satisfied the above relation is 3. Hence, we require 3 parity bits p1, p2, and p3. Therefore, the number of bits in Hamming code will be 7, since there are 4 bits in binary code and 3 parity bits. We have to place the parity bits and bits of binary code in the Hamming code as shown below.
The 7-bit Hamming code is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}=d_{4}d_{3}d_{2}p_{3}d_{1}p_{2}bp_{1}$
By substituting the bits of binary code, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1} = 100p_{3}Op_{2}p_{1}$. Now, let us find the parity bits.
$$p_{1}=b_{7}\oplus b_{5}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{2}=b_{7}\oplus b_{6}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{3}=b_{7}\oplus b_{6}\oplus b_{5}=1 \oplus 0 \oplus 0=1$$
By substituting these parity bits, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$.
Example 2
In the above example, we got the Hamming code as $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$. Now, let us find the error position when the code received is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001111$.
Now, let us find the check bits.
$$c_{1}=b_{7}\oplus b_{5}\oplus b_{3}\oplus b_{1}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{2}=b_{7}\oplus b_{6}\oplus b_{3}\oplus b_{2}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{3}=b_{7}\oplus b_{6}\oplus b_{5}\oplus b_{4}=1 \oplus 0 \oplus 0 \oplus1 =0$$
The decimal value of check bits gives the position of error in received Hamming code.
$$c_{3}c_{2}c_{1} = \left ( 011 \right )_{2}=\left ( 3 \right )_{10}$$
Therefore, the error present in third bit (b3) of Hamming code. Just complement the value present in that bit and remove parity bits in order to get the original binary code.
Boolean Algebra is an algebra, which deals with binary numbers & binary variables. Hence, it is also called as Binary Algebra or logical Algebra. A mathematician, named George Boole had developed this algebra in 1854. The variables used in this algebra are also called as Boolean variables.
The range of voltages corresponding to Logic ‘High’ is represented with ‘1’ and the range of voltages corresponding to logic ‘Low’ is represented with ‘0’.
Postulates and Basic Laws of Boolean Algebra
In this section, let us discuss about the Boolean postulates and basic laws that are used in Boolean algebra. These are useful in minimizing Boolean functions.
Boolean Postulates
Consider the binary numbers 0 and 1, Boolean variable (x) and its complement (x’). Either the Boolean variable or complement of it is known as literal. The four possible logical OR operations among these literals and binary numbers are shown below.
x + 0 = x
x + 1 = 1
x + x = x
x + x '= 1
Da mesma forma, os quatro possíveis logical AND operações entre esses literais e números binários são mostradas abaixo.
x.1 = x
x.0 = 0
xx = x
x.x '= 0
Esses são os postulados booleanos simples. Podemos verificar esses postulados facilmente, substituindo a variável booleana por '0' ou '1'.
Note- O complemento do complemento de qualquer variável booleana é igual à própria variável. ou seja, (x ')' = x.
Leis Básicas da Álgebra Booleana
A seguir estão as três leis básicas da Álgebra Booleana.
- Lei comutativa
- Lei associativa
- Lei distributiva
Lei comutativa
Se qualquer operação lógica de duas variáveis booleanas der o mesmo resultado, independentemente da ordem dessas duas variáveis, então essa operação lógica é considerada Commutative. As operações lógicas OR & lógicas AND de duas variáveis booleanas x e y são mostradas abaixo
x + y = y + x
xy = yx
O símbolo '+' indica operação lógica OR. Da mesma forma, o símbolo '.' indica a operação lógica AND e sua representação é opcional. A lei comutativa obedece a operações lógicas OR e AND lógicas.
Direito Associativo
Se uma operação lógica de quaisquer duas variáveis booleanas for realizada primeiro e, em seguida, a mesma operação for realizada com a variável restante fornecer o mesmo resultado, então essa operação lógica é considerada Associative. As operações lógicas OR e AND lógicas de três variáveis booleanas x, y e z são mostradas abaixo.
x + (y + z) = (x + y) + z
x. (yz) = (xy) .z
A lei associativa obedece a operações lógicas OR e AND lógicas.
Lei Distributiva
Se qualquer operação lógica pode ser distribuída para todos os termos presentes na função booleana, então essa operação lógica é considerada Distributive. A distribuição das operações lógicas OR e AND lógico de três variáveis booleanas x, y e z são mostradas abaixo.
x. (y + z) = xy + xz
x + (yz) = (x + y). (x + z)
A lei distributiva obedece a operações lógicas OR e AND lógicas.
Estas são as leis básicas da álgebra booleana. Podemos verificar essas leis facilmente, substituindo as variáveis booleanas por '0' ou '1'.
Teoremas da Álgebra Booleana
Os dois teoremas a seguir são usados na álgebra booleana.
- Teorema da dualidade
- Teorema de DeMorgan
Teorema da Dualidade
Este teorema afirma que o dualda função booleana é obtido trocando o operador lógico AND com o operador lógico OR e zeros com uns. Para cada função booleana, haverá uma função Dual correspondente.
Vamos fazer as equações booleanas (relações) que discutimos na seção de postulados booleanos e leis básicas em dois grupos. A tabela a seguir mostra esses dois grupos.
| Grupo 1 | Grupo 2 |
|---|---|
| x + 0 = x | x.1 = x |
| x + 1 = 1 | x.0 = 0 |
| x + x = x | xx = x |
| x + x '= 1 | x.x '= 0 |
| x + y = y + x | xy = yx |
| x + (y + z) = (x + y) + z | x. (yz) = (xy) .z |
| x. (y + z) = xy + xz | x + (yz) = (x + y). (x + z) |
Em cada linha, existem duas equações booleanas e elas são duais entre si. Podemos verificar todas essas equações booleanas do Grupo1 e Grupo2 usando o teorema da dualidade.
Teorema de DeMorgan
Este teorema é útil para encontrar o complement of Boolean function. Ele afirma que o complemento do OR lógico de pelo menos duas variáveis booleanas é igual ao AND lógico de cada variável complementada.
O teorema de DeMorgan com 2 variáveis booleanas x e y pode ser representado como
(x + y) '= x'.y'
O dual da função booleana acima é
(xy) '= x' + y '
Portanto, o complemento de AND lógico de duas variáveis booleanas é igual ao OR lógico de cada variável complementada. Da mesma forma, podemos aplicar o teorema de DeMorgan para mais de 2 variáveis booleanas também.
Simplificação de funções booleanas
Até agora, discutimos os postulados, leis básicas e teoremas da álgebra booleana. Agora, vamos simplificar algumas funções booleanas.
Exemplo 1
Deixe-nos simplify a função booleana, f = p'qr + pq'r + pqr '+ pqr
Podemos simplificar essa função em dois métodos.
Method 1
Dada a função booleana, f = p'qr + pq'r + pqr '+ pqr.
Step 1- No primeiro e segundo termos r é comum e no terceiro e quarto termos pq é comum. Então, pegue os termos comuns usandoDistributive law.
⇒ f = (p'q + pq ') r + pq (r' + r)
Step 2- Os termos presentes no primeiro parêntese podem ser simplificados para a operação Ex-OR. Os termos presentes no segundo parêntese podem ser simplificados para '1' usandoBoolean postulate
⇒ f = (p ⊕q) r + pq (1)
Step 3- O primeiro termo não pode ser mais simplificado. Mas, o segundo termo pode ser simplificado para pq usandoBoolean postulate.
⇒ f = (p ⊕q) r + pq
Portanto, a função booleana simplificada é f = (p⊕q)r + pq
Method 2
Dada a função booleana, f = p'qr + pq'r + pqr '+ pqr.
Step 1 - Use o Boolean postulate, x + x = x. Isso significa que a operação lógica OR com qualquer variável booleana 'n' vezes será igual à mesma variável. Então, podemos escrever o último termo pqr mais duas vezes.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - Use Distributive lawpara 1º e 4º termos, 2º e 5º termos, 3º e 6º termos.
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r)
Step 3 - Use Boolean postulate, x + x '= 1 para simplificar os termos presentes em cada parêntese.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - Use Boolean postulate, x.1 = x para simplificar os três termos acima.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Portanto, a função booleana simplificada é f = pq + qr + pr.
Portanto, obtivemos duas funções booleanas diferentes após simplificar a função booleana fornecida em cada método. Funcionalmente, essas duas funções booleanas são iguais. Portanto, com base no requisito, podemos escolher uma dessas duas funções booleanas.
Exemplo 2
Deixe-nos encontrar o complement da função booleana, f = p'q + pq '.
O complemento da função booleana é f '= (p'q + pq') '.
Step 1 - Use o teorema de DeMorgan, (x + y) '= x'.y'.
⇒ f '= (p'q)'. (Pq ')'
Step 2 - Use o teorema de DeMorgan, (xy) '= x' + y '
⇒ f '= {(p') '+ q'}. {P '+ (q') '}
Step3 - Use o postulado booleano, (x ')' = x.
⇒ f '= {p + q'}. {P '+ q}
⇒ f '= pp' + pq + p'q '+ qq'
Step 4 - Use o postulado booleano, xx '= 0.
⇒ f = 0 + pq + p'q '+ 0
⇒ f = pq + p'q '
Portanto, o complement da função booleana, p'q + pq 'é pq + p’q’.
Obteremos quatro termos de produto booleanos combinando duas variáveis xey com operação lógica AND. Esses termos de produto booleanos são chamados demin terms ou standard product terms. Os termos mínimos são x'y ', x'y, xy' e xy.
Da mesma forma, obteremos quatro termos de soma booleana combinando duas variáveis xey com operação lógica OR. Esses termos de soma booleana são chamados deMax terms ou standard sum terms. Os termos máximos são x + y, x + y ', x' + y e x '+ y'.
A tabela a seguir mostra a representação de termos mínimos e termos MAX para 2 variáveis.
| x | y | Termos mínimos | Termos máximos |
|---|---|---|---|
| 0 | 0 | m 0 = x'y ' | M 0 = x + y |
| 0 | 1 | m 1 = x'y | M 1 = x + y? |
| 1 | 0 | m 2 = xy ' | M 2 = x' + y |
| 1 | 1 | m 3 = xy | M 3 = x '+ y' |
Se a variável binária for '0', então ela é representada como complemento da variável em termo mínimo e como a própria variável em termo máximo. Da mesma forma, se a variável binária é '1', então ela é representada como complemento da variável no termo Max e como a própria variável no termo min.
Na tabela acima, podemos facilmente notar que os termos mínimos e os termos máximos são complementares um do outro. Se houver 'n' variáveis booleanas, haverá 2 n termos mínimos e 2 n termos máximos.
Formulários canônicos de SoP e PoS
Uma tabela verdade consiste em um conjunto de entradas e saídas. Se houver 'n' variáveis de entrada, haverá 2 n combinações possíveis com zeros e uns. Portanto, o valor de cada variável de saída depende da combinação das variáveis de entrada. Portanto, cada variável de saída terá '1' para alguma combinação de variáveis de entrada e '0' para alguma outra combinação de variáveis de entrada.
Portanto, podemos expressar cada variável de saída de duas maneiras.
- Formulário de SoP canônico
- Formulário PoS canônico
Formulário de SoP canônico
A forma Canonical SoP significa a forma Canonical Soma of Products. Nesse formulário, cada termo do produto contém todos os literais. Portanto, esses termos de produto nada mais são do que os termos mínimos. Portanto, a forma canônica de SoP também é chamada desum of min terms Formato.
Primeiro, identifique os termos mínimos para os quais a variável de saída é um e depois faça o OR lógico desses termos mínimos para obter a expressão booleana (função) correspondente a essa variável de saída. Esta função booleana estará na forma de soma de termos mínimos.
Siga o mesmo procedimento para outras variáveis de saída também, se houver mais de uma variável de saída.
Exemplo
Considere o seguinte truth table.
| Entradas | Resultado | ||
|---|---|---|---|
| p | q | r | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Aqui, a saída (f) é '1' para quatro combinações de entradas. Os termos min correspondentes são p'qr, pq'r, pqr ', pqr. Fazendo OR lógico desses quatro termos mínimos, obteremos a função booleana de saída (f).
Portanto, a função booleana de saída é, f = p'qr + pq'r + pqr '+ pqr. Isto é ocanonical SoP formde saída, f. Também podemos representar essa função seguindo duas notações.
$$f = m_{3}+m_{5}+m_{6}+m_{7}$$
$$f = \sum m\left ( 3,5,6,7 \right )$$
Em uma equação, representamos a função como a soma dos respectivos termos mínimos. Em outra equação, usamos o símbolo para a soma desses termos mínimos.
Formulário PoS canônico
A forma PoS canônica significa a forma de produto canônico de somas. Nesta forma, cada termo de soma contém todos os literais. Portanto, esses termos de soma nada mais são do que os termos máximos. Portanto, o formulário PoS canônico também é chamado deproduct of Max terms Formato.
Primeiro, identifique os termos máximos para os quais a variável de saída é zero e, em seguida, faça o AND lógico desses termos máximos para obter a expressão booleana (função) correspondente a essa variável de saída. Esta função booleana estará na forma de produto de termos máximos.
Siga o mesmo procedimento para outras variáveis de saída também, se houver mais de uma variável de saída.
Example
Considere a mesma tabela verdade do exemplo anterior. Aqui, a saída (f) é '0' para quatro combinações de entradas. Os termos máximos correspondentes são p + q + r, p + q + r ', p + q' + r, p '+ q + r. Fazendo o AND lógico desses quatro termos máximos, obteremos a função booleana de saída (f).
Portanto, a função booleana de saída é, f = (p + q + r). (P + q + r '). (P + q' + r). (P '+ q + r). Isto é ocanonical PoS formde saída, f. Também podemos representar essa função seguindo duas notações.
$$f=M_{0}.M_{1}.M_{2}.M_{4}$$
$$f=\prod M\left ( 0,1,2,4 \right )$$
Em uma equação, representamos a função como produto dos respectivos termos máximos. Em outra equação, usamos o símbolo para a multiplicação desses termos máximos.
A função booleana, f = (p + q + r). (P + q + r '). (P + q' + r). (P '+ q + r) é o dual da função booleana, f = p'qr + pq'r + pqr '+ pqr.
Portanto, os formulários canônicos de SoP e PoS canônicos são Dualum para o outro. Funcionalmente, essas duas formas são iguais. Com base no requisito, podemos usar um desses dois formulários.
Formulários padrão de SoP e PoS
Discutimos duas formas canônicas de representar as saídas booleanas. Da mesma forma, existem duas formas padrão de representar a (s) saída (s) booleana (s). Estas são a versão simplificada dos formulários canônicos.
- Formulário SoP padrão
- Formulário de PoS padrão
Discutiremos sobre portas lógicas em capítulos posteriores. O principaladvantagedas formas padrão é que o número de entradas aplicadas às portas lógicas pode ser minimizado. Às vezes, haverá redução no número total de portas lógicas necessárias.
Formulário SoP padrão
O formulário padrão do SoP significa Standard Sum of ProductsFormato. Nesse formulário, cada termo do produto não precisa conter todos os literais. Portanto, os termos do produto podem ou não ser os termos mínimos. Portanto, o formulário SoP padrão é a forma simplificada do formulário SoP canônico.
Obteremos a forma padrão SoP da variável de saída em duas etapas.
- Obtenha a forma canônica de SoP da variável de saída
- Simplifique a função booleana acima, que está na forma SoP canônica.
Siga o mesmo procedimento para outras variáveis de saída também, se houver mais de uma variável de saída. Às vezes, pode não ser possível simplificar o formulário SoP canônico. Nesse caso, os formulários SoP canônico e padrão são iguais.
Example
Converta a seguinte função booleana no formato SoP padrão.
f = p'qr + pq'r + pqr '+ pqr
A função booleana fornecida está no formato SoP canônico. Agora, temos que simplificar esta função booleana para obter a forma SoP padrão.
Step 1 - Use o Boolean postulate, x + x = x. Isso significa que a operação lógica OR com qualquer variável booleana 'n' vezes será igual à mesma variável. Então, podemos escrever o último termo pqr mais duas vezes.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - Use Distributive lawpara 1º e 4º termos, 2º e 5º termos, 3º e 6º termos.
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r)
Step 3 - Use Boolean postulate, x + x '= 1 para simplificar os termos presentes em cada parêntese.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - Use Boolean postulate, x.1 = x para simplificar acima de três termos.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Esta é a função booleana simplificada. Portanto, ostandard SoP form correspondente à forma canônica de SoP dada é f = pq + qr + pr
Formulário de PoS padrão
Formulário de PoS padrão significa Standard Product of SumsFormato. Nessa forma, cada termo de soma não precisa conter todos os literais. Portanto, os termos de soma podem ou não ser os termos máximos. Portanto, o formulário PoS padrão é a forma simplificada do formulário PoS canônico.
Obteremos a forma PoS padrão da variável de saída em duas etapas.
- Obtenha a forma PoS canônica da variável de saída
- Simplifique a função booleana acima, que está na forma PoS canônica.
Siga o mesmo procedimento para outras variáveis de saída também, se houver mais de uma variável de saída. Às vezes, pode não ser possível simplificar o formulário PoS canônico. Nesse caso, os formulários de PoS canônicos e padrão são iguais.
Example
Converta a seguinte função booleana no formato PoS padrão.
f = (p + q + r). (p + q + r '). (p + q' + r). (p '+ q + r)
A função booleana fornecida está na forma PoS canônica. Agora, temos que simplificar esta função booleana para obter a forma PoS padrão.
Step 1 - Use o Boolean postulate, xx = x. Isso significa que a operação Lógica AND com qualquer variável booleana 'n' vezes será igual à mesma variável. Portanto, podemos escrever o primeiro termo p + q + r mais duas vezes.
⇒ f = (p + q + r). (P + q + r). (P + q + r). (P + q + r '). (P + q' + r). (P '+ q + r)
Step 2 - Use Distributive law,x + (yz) = (x + y). (x + z) para 1º e 4º parênteses, 2º e 5º parênteses, 3º e 6º parênteses.
⇒ f = (p + q + rr '). (P + r + qq'). (Q + r + pp ')
Step 3 - Use Boolean postulate, x.x '= 0 para simplificar os termos presentes em cada parêntese.
⇒ f = (p + q + 0). (P + r + 0). (Q + r + 0)
Step 4 - Use Boolean postulate, x + 0 = x para simplificar os termos presentes em cada parêntese
⇒ f = (p + q). (P + r). (Q + r)
⇒ f = (p + q). (Q + r). (P + r)
Esta é a função booleana simplificada. Portanto, ostandard PoS form correspondente ao dado formulário PoS canônico é f = (p + q).(q + r).(p + r). Isto é odual da função booleana, f = pq + qr + pr.
Portanto, as formas padrão do SoP e do PoS padrão são duplas entre si.
Nos capítulos anteriores, simplificamos as funções booleanas usando postulados e teoremas booleanos. É um processo demorado e temos que reescrever as expressões simplificadas após cada etapa.
Para superar essa dificuldade, Karnaughintroduziu um método para simplificação de funções booleanas de forma fácil. Este método é conhecido como método do mapa de Karnaugh ou método do K-map. É um método gráfico, que consiste em 2 n células para 'n' variáveis. As células adjacentes diferem apenas na posição de um único bit.
K-Maps para 2 a 5 variáveis
O método K-Map é mais adequado para minimizar funções booleanas de 2 variáveis para 5 variáveis. Agora, vamos discutir sobre os K-Maps para 2 a 5 variáveis, uma por uma.
2 Variáveis K-Map
O número de células em 2 variáveis K-map é quatro, já que o número de variáveis é dois. A figura a seguir mostra2 variable K-Map.
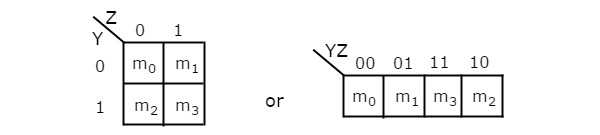
Existe apenas uma possibilidade de agrupar 4 termos mínimos adjacentes.
As combinações possíveis de agrupamento de 2 termos min adjacentes são {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) e (m 1 , m 3 )}.
3 Variáveis K-Map
O número de células em 3 variáveis K-map é oito, já que o número de variáveis é três. A figura a seguir mostra3 variable K-Map.
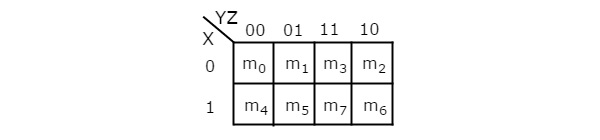
Existe apenas uma possibilidade de agrupar 8 termos mínimos adjacentes.
As combinações possíveis de agrupamento de 4 termos min adjacentes são {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m 5 ), (m 1 , m 3 , m 5 , m 7 ), (m 3 , m 2 , m 7 , m 6 ) e (m 2 , m 0 , m 6 , m 4 )}.
As combinações possíveis de agrupamento de 2 termos min adjacentes são {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 ) , (m 5 , m 7 ), (m 7 , m 6 ), (m 6 , m 4 ), (m 0 , m 4 ), (m 1 , m 5 ), (m 3 , m 7 ) e ( m 2 , m 6 )}.
Se x = 0, então o K-map de 3 variáveis torna-se o K-map de 2 variáveis.
4 Variáveis K-Map
O número de células em 4 variáveis K-map é dezesseis, já que o número de variáveis é quatro. A figura a seguir mostra4 variable K-Map.
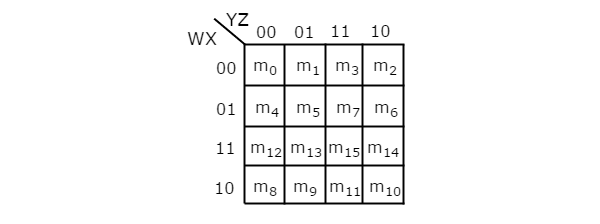
Existe apenas uma possibilidade de agrupar 16 termos mínimos adjacentes.
Sejam R 1 , R 2 , R 3 e R 4 representem os termos mínimos da primeira linha, segunda linha, terceira linha e quarta linha, respectivamente. Da mesma forma, C 1 , C 2 , C 3 e C 4 representam os termos mínimos da primeira coluna, segunda coluna, terceira coluna e quarta coluna, respectivamente. As combinações possíveis de agrupamento de 8 termos min adjacentes são {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 ) , (C 2 , C 3 ), (C 3 , C 4 ), (C 4 , C 1 )}.
Se w = 0, então o mapa K de 4 variáveis se torna o mapa K de 3 variáveis.
5 Variável K-Map
O número de células em 5 variáveis K-map é trinta e dois, uma vez que o número de variáveis é 5. A figura a seguir mostra 5 variable K-Map.

Existe apenas uma possibilidade de agrupar 32 termos mínimos adjacentes.
Existem duas possibilidades de agrupar 16 termos mínimos adjacentes. ou seja, agrupamento de termos mínimos de m 0 a m 15 e m 16 a m 31 .
Se v = 0, então o K-map de 5 variáveis torna-se o K-map de 4 variáveis.
Acima em todos os K-maps, usamos exclusivamente a notação de termos mínimos. Da mesma forma, você pode usar exclusivamente a notação de termos máximos.
Minimização de funções booleanas usando K-Maps
Se considerarmos a combinação de entradas para as quais a função booleana é '1', então obteremos a função booleana, que está em standard sum of products formulário após simplificar o K-map.
Da mesma forma, se considerarmos a combinação de entradas para as quais a função booleana é '0', então obteremos a função booleana, que está em standard product of sums formulário após simplificar o K-map.
Siga estes rules for simplifying K-maps a fim de obter a soma padrão do formulário de produtos.
Selecione o respectivo K-map com base no número de variáveis presentes na função booleana.
Se a função booleana for dada como a soma da forma de termos mínimos, coloque-os nas respectivas células de termos mínimos no K-map. Se a função booleana for dada como a forma da soma dos produtos, coloque aqueles em todas as células possíveis do K-map para as quais os termos do produto dados são válidos.
Verifique a possibilidade de agrupar o número máximo de adjacentes. Deve ser potências de dois. Comece com a maior potência de dois e pelo menos a potência de dois. A maior potência é igual ao número de variáveis consideradas no K-map e a menor potência é zero.
Cada agrupamento fornecerá um termo literal ou um termo de produto. É conhecido comoprime implicant. O implicante principal é dito seressential prime implicant, se pelo menos o único '1' não for coberto por nenhum outro agrupamento, mas apenas esse agrupamento abrange.
Anote todos os implicantes primos e implicantes primos essenciais. A função booleana simplificada contém todos os implicantes primos essenciais e apenas os implicantes primos necessários.
Note 1 - Se as saídas não forem definidas para alguma combinação de entradas, esses valores de saída serão representados com don’t care symbol ‘x’. Isso significa que podemos considerá-los como '0' ou '1'.
Note 2- Se os termos não importados também estiverem presentes, coloque 'x' não importados nas respectivas células do K-map. Considere apenas os irrelevantes 'x' que são úteis para agrupar o número máximo de unidades adjacentes. Nesses casos, trate o valor irrelevante como '1'.
Exemplo
Deixe-nos simplify a seguinte função booleana, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ usando K-map.
A função booleana fornecida está na forma de soma dos produtos. Tem 4 variáveis W, X, Y e Z. Portanto, exigimos4 variable K-map. o4 variable K-map com aqueles correspondentes aos termos do produto fornecidos é mostrado na figura a seguir.
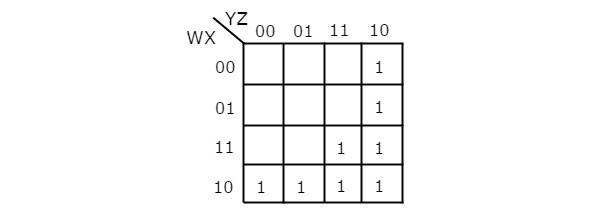
Aqui, 1s são colocados nas seguintes células do K-map.
As células, que são comuns à interseção da linha 4 e colunas 1 e 2, correspondem ao termo do produto, WX’Y’.
As células, que são comuns à interseção das Linhas 3 e 4 e colunas 3 e 4, correspondem ao termo do produto, WY.
As células, que são comuns à interseção das Linhas 1 e 2 e da coluna 4, correspondem ao termo do produto, W’YZ’.
Não há possibilidade de agrupar 16 adjacentes ou 8 adjacentes. Existem três possibilidades de agrupar 4 adjacentes. Após esses três agrupamentos, não há mais nenhum agrupado. Portanto, não precisamos verificar o agrupamento de 2 adjacentes. o4 variable K-map com esses três groupings é mostrado na figura a seguir.

Aqui, temos três implicantes primos WX ', WY e YZ'. Todos esses implicantes primários sãoessential pelos seguintes motivos.
Dois uns (m8 & m9)do agrupamento da quarta linha não são cobertos por nenhum outro agrupamento. Apenas o quarto agrupamento de linhas cobre esses dois.
Um único (m15)de agrupamento de forma quadrada não é coberto por nenhum outro agrupamento. Apenas o agrupamento de forma quadrada cobre aquele.
Dois uns (m2 & m6)do quarto agrupamento de colunas não são cobertos por nenhum outro agrupamento. Apenas o quarto agrupamento de colunas cobre esses dois.
Portanto, o simplified Boolean function é
f = WX’ + WY + YZ’
Siga estes rules for simplifying K-maps a fim de obter o produto padrão do formulário de somas.
Selecione o respectivo K-map com base no número de variáveis presentes na função booleana.
Se a função booleana for fornecida como produto da forma de termos Max, coloque os zeros nas respectivas células de termo Max no K-map. Se a função booleana é fornecida como produto da forma de somas, coloque os zeros em todas as células possíveis do K-map para as quais os termos de soma fornecidos são válidos.
Verifique as possibilidades de agrupar o número máximo de zeros adjacentes. Deve ser potências de dois. Comece com a maior potência de dois e pelo menos a potência de dois. A maior potência é igual ao número de variáveis consideradas no K-map e a menor potência é zero.
Cada agrupamento fornecerá um termo literal ou um termo de soma. É conhecido comoprime implicant. O implicante principal é dito seressential prime implicant, se pelo menos o único '0' não for coberto por nenhum outro agrupamento, mas apenas aquele agrupamento abrange.
Anote todos os implicantes primos e implicantes primos essenciais. A função booleana simplificada contém todos os implicantes primos essenciais e apenas os implicantes primos necessários.
Note- Se os termos não importados também estiverem presentes, coloque 'x' não importados nas respectivas células do K-map. Considere apenas os 'x' irrelevantes que são úteis para agrupar o número máximo de zeros adjacentes. Nesses casos, trate o valor irrelevante como '0'.
Exemplo
Deixe-nos simplify a seguinte função booleana, $f\left ( X,Y,Z \right )=\prod M\left ( 0,1,2,4 \right )$ usando K-map.
A função booleana fornecida é um produto da forma de termos máximos. Tem 3 variáveis X, Y e Z. Portanto, precisamos de 3 variáveis K-map. Os termos máximos fornecidos são M 0 , M 1 , M 2 e M 4 . Os 3variable K-map com zeros correspondendo aos termos máximos fornecidos é mostrado na figura a seguir.

Não há possibilidades de agrupar 8 zeros adjacentes ou 4 zeros adjacentes. Existem três possibilidades de agrupar 2 zeros adjacentes. Após esses três agrupamentos, não há mais nenhum zero como desagrupado. o3 variable K-map com esses três groupings é mostrado na figura a seguir.

Aqui, temos três implicantes primos X + Y, Y + Z & Z + X. Todos esses implicantes primos são essential porque um zero em cada agrupamento não é coberto por nenhum outro agrupamento, exceto com seus agrupamentos individuais.
Portanto, o simplified Boolean function é
f = (X + Y).(Y + Z).(Z + X)
Desta forma, podemos simplificar facilmente as funções booleanas em até 5 variáveis usando o método K-map. Para mais de 5 variáveis, é difícil simplificar as funções usando o K-Maps. Porque, o número decells no K-map obtém doubled incluindo uma nova variável.
Devido a esta verificação e agrupamento de uns adjacentes (termos mínimos) ou zeros adjacentes (termos máximos) será complicado. Vamos discutirTabular method no próximo capítulo para superar as dificuldades do método K-map.
No capítulo anterior, discutimos o método K-map, que é um método conveniente para minimizar funções booleanas até 5 variáveis. Porém, é difícil simplificar as funções booleanas com mais de 5 variáveis usando este método.
O método tabular de Quine-McClukey é um método tabular baseado no conceito de implicantes primários. Nós sabemos issoprime implicant é um termo de produto (ou soma), que não pode ser reduzido ainda mais combinando-se com qualquer outro produto (ou soma) de termos da função booleana fornecida.
Este método tabular é útil para obter os implicantes primários usando repetidamente a seguinte identidade booleana.
xy + xy '= x (y + y') = x.1 = x
Procedimento do Método Tabular Quine-McCluskey
Siga estas etapas para simplificar as funções booleanas usando o método tabular Quine-McClukey.
Step 1 - Organize os termos mínimos fornecidos em um ascending ordere faça os grupos com base no número de unidades presentes em suas representações binárias. Então, haveráat most ‘n+1’ groups se houver 'n' variáveis booleanas em uma função booleana ou 'n' bits no equivalente binário de termos mínimos.
Step 2 - Compare os termos mínimos presentes em successive groups. Se houver uma mudança na posição de apenas um bit, considere o par desses dois termos mínimos. Coloque este símbolo '_' na posição do bit diferente e mantenha os bits restantes como estão.
Step 3 - Repita a etapa 2 com os termos recém-formados até obtermos todos prime implicants.
Step 4 - Formule o prime implicant table. Ele consiste em um conjunto de linhas e colunas. Os implicantes primários podem ser colocados em linhas e os termos mínimos podem ser colocados em colunas. Coloque '1' nas células correspondentes aos termos mínimos que são cobertos em cada implicante primo.
Step 5- Encontre os implicantes primários essenciais observando cada coluna. Se o termo mínimo for coberto apenas por um implicante primo, então ele éessential prime implicant. Esses implicantes primos essenciais farão parte da função booleana simplificada.
Step 6- Reduza a tabela do implicante primo removendo a linha de cada implicante primo essencial e as colunas correspondentes aos termos min que são cobertos naquele implicante primo essencial. Repita a etapa 5 para a tabela implicante principal reduzida. Pare este processo quando todos os termos mínimos de determinada função booleana terminarem.
Exemplo
Deixe-nos simplify a seguinte função booleana, $f\left ( W,X,Y,Z \right )=\sum m\left ( 2,6,8,9,10,11,14,15 \right )$ usando o método tabular Quine-McClukey.
A função booleana fornecida está em sum of min termsFormato. Ele tem 4 variáveis W, X, Y e Z. Os termos mínimos fornecidos são 2, 6, 8, 9, 10, 11, 14 e 15. A ordem crescente desses termos mínimos com base no número de alguns presentes em seus equivalente binário é 2, 8, 6, 9, 10, 11, 14 e 15. A seguinte tabela mostra estesmin terms and their equivalent binary representações.
| Nome do grupo | Termos mínimos | W | X | Y | Z |
|---|---|---|---|---|---|
| GA1 | 2 | 0 | 0 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | |
| GA2 | 6 | 0 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | |
| 10 | 1 | 0 | 1 | 0 | |
| 11 | 1 | 0 | 1 | 1 | |
| 14 | 1 | 1 | 1 | 0 | |
| GA4 | 15 | 1 | 1 | 1 | 1 |
Os termos mínimos fornecidos são organizados em 4 grupos com base no número de uns presentes em seus equivalentes binários. A tabela a seguir mostra os possíveismerging of min terms de grupos adjacentes.
| Nome do grupo | Termos mínimos | W | X | Y | Z |
|---|---|---|---|---|---|
| GB1 | 2,6 | 0 | - | 1 | 0 |
| 2,10 | - | 0 | 1 | 0 | |
| 8,9 | 1 | 0 | 0 | - | |
| 8,10 | 1 | 0 | - | 0 | |
| GB2 | 6,14 | - | 1 | 1 | 0 |
| 9,11 | 1 | 0 | - | 1 | |
| 10,11 | 1 | 0 | 1 | - | |
| 10,14 | 1 | - | 1 | 0 | |
| 11,15 | 1 | - | 1 | 1 | |
| 14,15 | 1 | 1 | 1 | - |
Os termos mínimos, que diferem em apenas uma posição de um bit dos grupos adjacentes, são mesclados. Esse bit diferente é representado com este símbolo, '-'. Nesse caso, existem três grupos e cada grupo contém combinações de dois termos mínimos. A tabela a seguir mostra os possíveismerging of min term pairs de grupos adjacentes.
| Nome do grupo | Termos mínimos | W | X | Y | Z |
|---|---|---|---|---|---|
| GB1 | 2,6,10,14 | - | - | 1 | 0 |
| 2,10,6,14 | - | - | 1 | 0 | |
| 8,9,10,11 | 1 | 0 | - | - | |
| 8,10,9,11 | 1 | 0 | - | - | |
| GB2 | 10,11,14,15 | 1 | - | 1 | - |
| 10,14,11,15 | 1 | - | 1 | - |
Os grupos sucessivos de pares de termos mínimos, que diferem na posição de apenas um bit, são mesclados. Esse bit diferente é representado com este símbolo, '-'. Nesse caso, existem dois grupos e cada grupo contém combinações de quatro termos mínimos. Aqui, essas combinações de termos de 4 minutos estão disponíveis em duas linhas. Portanto, podemos remover as linhas repetidas. A tabela reduzida após a remoção das linhas redundantes é mostrada abaixo.
| Nome do grupo | Termos mínimos | W | X | Y | Z |
|---|---|---|---|---|---|
| GC1 | 2,6,10,14 | - | - | 1 | 0 |
| 8,9,10,11 | 1 | 0 | - | - | |
| GC2 | 10,11,14,15 | 1 | - | 1 | - |
A fusão posterior das combinações de termos mínimos de grupos adjacentes não é possível, uma vez que eles diferem em mais de uma posição de bit. Existem três linhas na tabela acima. Portanto, cada linha dará um implicante primo. Portanto, oprime implicants são YZ ', WX' e WY.
o prime implicant table é mostrado abaixo.
| Termos mínimos / Implicantes principais | 2 | 6 | 8 | 9 | 10 | 11 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|
| YZ’ | 1 | 1 | 1 | 1 | ||||
| WX’ | 1 | 1 | 1 | 1 | ||||
| WY | 1 | 1 | 1 | 1 |
Os implicantes primários são colocados em linhas e os termos mínimos são colocados em colunas. 1s são colocados nas células comuns das linhas implicantes principais e nas colunas de termo mínimo correspondentes.
Os termos mínimos 2 e 6 são cobertos apenas por um implicante principal YZ’. Então, é umessential prime implicant. Isso fará parte da função booleana simplificada. Agora, remova esta linha principal implicante e as colunas de termo mínimo correspondentes. A tabela de implicantes primários reduzida é mostrada abaixo.
| Termos mínimos / Implicantes principais | 8 | 9 | 11 | 15 |
|---|---|---|---|---|
| WX’ | 1 | 1 | 1 | |
| WY | 1 | 1 |
Os termos mínimos 8 e 9 são cobertos apenas por um implicante principal WX’. Então, é umessential prime implicant. Isso fará parte da função booleana simplificada. Agora, remova esta linha principal implicante e as colunas de termo mínimo correspondentes. A tabela de implicantes primários reduzida é mostrada abaixo.
| Termos mínimos / Implicantes principais | 15 |
|---|---|
| WY | 1 |
O termo mínimo 15 é coberto apenas por um implicante principal WY. Então, é umessential prime implicant. Isso fará parte da função booleana simplificada.
Neste exemplo de problema, obtivemos três implicantes primos e todos os três são essenciais. Portanto, osimplified Boolean function é
f(W,X,Y,Z) = YZ’ + WX’ + WY.
Os circuitos eletrônicos digitais operam com tensões de two logic levelsa saber Logic Low e Logic High. A faixa de tensões correspondente ao Logic Low é representada por '0'. Da mesma forma, a faixa de tensões correspondente a Logic High é representada por '1'.
O circuito eletrônico digital básico que tem uma ou mais entradas e saída única é conhecido como Logic gate. Conseqüentemente, as portas lógicas são os blocos de construção de qualquer sistema digital. Podemos classificar essas portas lógicas nas três categorias a seguir.
- Portões básicos
- Portões universais
- Portões especiais
Agora, vamos discutir sobre as portas lógicas que vêm em cada categoria, uma por uma.
Portões básicos
Nos capítulos anteriores, aprendemos que as funções booleanas podem ser representadas na forma de soma de produtos ou em forma de produto de soma com base no requisito. Portanto, podemos implementar essas funções booleanas usando portas básicas. As portas básicas são portas AND, OR & NOT.
E portão
Uma porta AND é um circuito digital que tem duas ou mais entradas e produz uma saída, que é o logical ANDde todas essas entradas. É opcional representar oLogical AND com o símbolo '.'.
A tabela a seguir mostra o truth table de porta AND de 2 entradas.
| UMA | B | Y = AB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Aqui A, B são as entradas e Y é a saída de duas entradas AND gate. Se ambas as entradas forem '1', então apenas a saída Y será '1'. Para combinações restantes de entradas, a saída, Y é '0'.
A figura a seguir mostra o symbol de uma porta AND, que tem duas entradas A, B e uma saída, Y.

Esta porta AND produz uma saída (Y), que é o logical ANDde duas entradas A, B. Da mesma forma, se houver 'n' entradas, a porta AND produzirá uma saída, que é o AND lógico de todas essas entradas. Isso significa que a saída da porta AND será '1', quando todas as entradas forem '1'.
OU portão
Uma porta OR é um circuito digital que possui duas ou mais entradas e produz uma saída, que é o OR lógico de todas essas entradas. estelogical OR é representado com o símbolo '+'.
A tabela a seguir mostra o truth table de porta OR de 2 entradas.
| UMA | B | Y = A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output of two input OR gate. If both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.
The following figure shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.

This OR gate produces an output (Y), which is the logical OR of two inputs A, B. Similarly, if there are ‘n’ inputs, then the OR gate produces an output, which is the logical OR of all those inputs. That means, the output of an OR gate will be ‘1’, when at least one of those inputs is ‘1’.
NOT gate
A NOT gate is a digital circuit that has single input and single output. The output of NOT gate is the logical inversion of input. Hence, the NOT gate is also called as inverter.
The following table shows the truth table of NOT gate.
| A | Y = A’ |
|---|---|
| 0 | 1 |
| 1 | 0 |
Here A and Y are the input and output of NOT gate respectively. If the input, A is ‘0’, then the output, Y is ‘1’. Similarly, if the input, A is ‘1’, then the output, Y is ‘0’.
The following figure shows the symbol of NOT gate, which is having one input, A and one output, Y.

This NOT gate produces an output (Y), which is the complement of input, A.
Universal gates
NAND & NOR gates are called as universal gates. Because we can implement any Boolean function, which is in sum of products form by using NAND gates alone. Similarly, we can implement any Boolean function, which is in product of sums form by using NOR gates alone.
NAND gate
NAND gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical AND of all those inputs.
The following table shows the truth table of 2-input NAND gate.
| A | B | Y = (A.B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just opposite to that of two input AND gate operation.
The following image shows the symbol of NAND gate, which is having two inputs A, B and one output, Y.
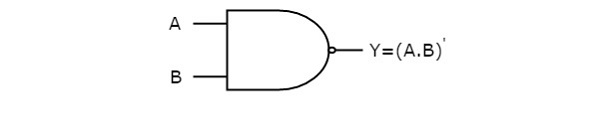
NAND gate operation is same as that of AND gate followed by an inverter. That’s why the NAND gate symbol is represented like that.
NOR gate
NOR gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical OR of all those inputs.
The following table shows the truth table of 2-input NOR gate
| A | B | Y = (A+B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output. If both inputs are ‘0’, then the output, Y is ‘1’. If at least one of the input is ‘1’, then the output, Y is ‘0’. This is just opposite to that of two input OR gate operation.
The following figure shows the symbol of NOR gate, which is having two inputs A, B and one output, Y.

NOR gate operation is same as that of OR gate followed by an inverter. That’s why the NOR gate symbol is represented like that.
Special Gates
Ex-OR & Ex-NOR gates are called as special gates. Because, these two gates are special cases of OR & NOR gates.
Ex-OR gate
The full form of Ex-OR gate is Exclusive-OR gate. Its function is same as that of OR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-OR gate.
| A | B | Y = A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input Ex-OR gate. The truth table of Ex-OR gate is same as that of OR gate for first three rows. The only modification is in the fourth row. That means, the output (Y) is zero instead of one, when both the inputs are one, since the inputs having even number of ones.
Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.
Below figure shows the symbol of Ex-OR gate, which is having two inputs A, B and one output, Y.

Ex-OR gate operation is similar to that of OR gate, except for few combination(s) of inputs. That’s why the Ex-OR gate symbol is represented like that. The output of Ex-OR gate is ‘1’, when odd number of ones present at the inputs. Hence, the output of Ex-OR gate is also called as an odd function.
Ex-NOR gate
The full form of Ex-NOR gate is Exclusive-NOR gate. Its function is same as that of NOR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-NOR gate.
| A | B | Y = A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output. The truth table of Ex-NOR gate is same as that of NOR gate for first three rows. The only modification is in the fourth row. That means, the output is one instead of zero, when both the inputs are one.
Therefore, the output of Ex-NOR gate is ‘1’, when both inputs are same. And it is zero, when both the inputs are different.
The following figure shows the symbol of Ex-NOR gate, which is having two inputs A, B and one output, Y.

Ex-NOR gate operation is similar to that of NOR gate, except for few combination(s) of inputs. That’s why the Ex-NOR gate symbol is represented like that. The output of Ex-NOR gate is ‘1’, when even number of ones present at the inputs. Hence, the output of Ex-NOR gate is also called as an even function.
From the above truth tables of Ex-OR & Ex-NOR logic gates, we can easily notice that the Ex-NOR operation is just the logical inversion of Ex-OR operation.
The maximum number of levels that are present between inputs and output is two in two level logic. That means, irrespective of total number of logic gates, the maximum number of Logic gates that are present (cascaded) between any input and output is two in two level logic. Here, the outputs of first level Logic gates are connected as inputs of second level Logic gate(s).
Consider the four Logic gates AND, OR, NAND & NOR. Since, there are 4 Logic gates, we will get 16 possible ways of realizing two level logic. Those are AND-AND, AND-OR, ANDNAND, AND-NOR, OR-AND, OR-OR, OR-NAND, OR-NOR, NAND-AND, NAND-OR, NANDNAND, NAND-NOR, NOR-AND, NOR-OR, NOR-NAND, NOR-NOR.
These two level logic realizations can be classified into the following two categories.
- Degenerative form
- Non-degenerative form
Degenerative Form
If the output of two level logic realization can be obtained by using single Logic gate, then it is called as degenerative form. Obviously, the number of inputs of single Logic gate increases. Due to this, the fan-in of Logic gate increases. This is an advantage of degenerative form.
Only 6 combinations of two level logic realizations out of 16 combinations come under degenerative form. Those are AND-AND, AND-NAND, OR-OR, OR-NOR, NAND-NOR, NORNAND.
In this section, let us discuss some realizations. Assume, A, B, C & D are the inputs and Y is the output in each logic realization.
AND-AND Logic
In this logic realization, AND gates are present in both levels. Below figure shows an example for AND-AND logic realization.

We will get the outputs of first level logic gates as $Y_{1}=AB$ and $Y_{2}=CD$
These outputs, $Y_{1}$ and $Y_{2}$ are applied as inputs of AND gate that is present in second level. So, the output of this AND gate is
$$Y=Y_{1}Y_{2}$$
Substitute $Y_{1}$ and $Y_{2}$ values in the above equation.
$$Y=\left ( AB \right )\left ( CD \right )$$
$\Rightarrow Y=ABCD$
Therefore, the output of this AND-AND logic realization is ABCD. This Boolean function can be implemented by using a 4 input AND gate. Hence, it is degenerative form.
AND-NAND Logic
In this logic realization, AND gates are present in first level and NAND gate(s) are present in second level. The following figure shows an example for AND-NAND logic realization.
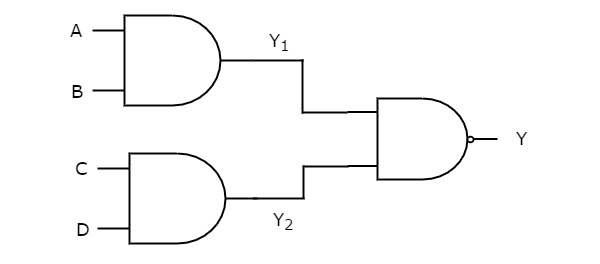
Anteriormente, obtivemos as saídas das portas lógicas de primeiro nível como $Y_{1} = AB$ e $Y_{2} = CD$
Essas saídas,$Y_{1}$ e $Y_{2}$são aplicados como entradas da porta NAND que está presente no segundo nível. Portanto, a saída desta porta NAND é
$$Y={\left ( Y_{1}Y_{2} \right )}'$$
Substituto $Y_{1}$ e $Y_{2}$ valores na equação acima.
$$Y={\left ( \left ( AB \right ) \left ( CD \right )\right )}'$$
$\Rightarrow Y={\left ( ABCD \right )}'$
Portanto, a saída desta realização da lógica AND-NAND é ${\left ( ABCD \right )}'$. Esta função booleana pode ser implementada usando uma porta NAND de 4 entradas. Portanto, édegenerative form.
Lógica OR-OR
Nesta realização lógica, portas OR estão presentes em ambos os níveis. A figura a seguir mostra um exemplo paraOR-OR logic realização.
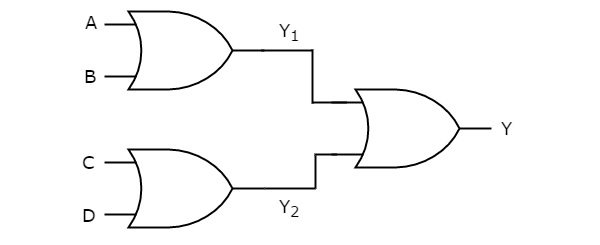
Obteremos as saídas das portas lógicas de primeiro nível como $Y_{1}=A+B$ e $Y_{2}=C+D$.
Essas saídas, $Y_{1}$ e $Y_{2}$são aplicados como entradas da porta OR que está presente no segundo nível. Portanto, a saída desta porta OR é
$$Y=Y_{1}+Y_{2}$$
Substituto $Y_{1}$ e $Y_{2}$ valores na equação acima.
$$Y=\left ( A+B \right )+\left ( C+D \right )$$
$\Rightarrow Y=A+B+C+D$
Portanto, a saída desta realização lógica OR-OR é A+B+C+D. Esta função booleana pode ser implementada usando uma porta OU de 4 entradas. Portanto, édegenerative form.
Da mesma forma, você pode verificar se as realizações restantes pertencem a esta categoria ou não.
Forma não degenerativa
Se a saída da realização lógica de dois níveis não pode ser obtida usando uma única porta lógica, então ela é chamada de non-degenerative form.
O restante 10 combinationsdas realizações lógicas de dois níveis vêm sob a forma não degenerativa. Esses são AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NANDOR, NAND-NAND, NOR-AND, NOR-OR, NOR-NOR.
Agora, vamos discutir algumas realizações. Suponha que A, B, C e D sejam as entradas e Y seja a saída em cada realização lógica.
Lógica AND-OR
Nesta realização lógica, as portas AND estão presentes no primeiro nível e as portas OR estão presentes no segundo nível. A figura abaixo mostra um exemplo paraAND-OR logic realização.

Anteriormente, obtivemos as saídas das portas lógicas de primeiro nível como $Y_{1} = AB$ e $Y_{2} = CD$.
Essas saídas, Y1 e Y2, são aplicadas como entradas da porta OR que está presente no segundo nível. Portanto, a saída desta porta OR é
$$Y=Y_{1}+Y_{2}$$
Substituto $Y_{1}$ e $Y_{2}$ valores na equação acima
$$Y=AB+CD$$
Portanto, a saída desta realização lógica AND-OR é AB+CD. Esta função booleana está emSum of ProductsFormato. Uma vez que não podemos implementá-lo usando uma única porta lógica, esta realização lógica AND-OR é umnon-degenerative form.
Lógica AND-NOR
Nesta realização lógica, as portas AND estão presentes no primeiro nível e as portas NOR estão presentes no segundo nível. A figura a seguir mostra um exemplo paraAND-NOR logic realização.

Conhecemos as saídas das portas lógicas de primeiro nível como $Y_{1} = AB$ e $Y_{2} = CD$
Essas saídas, Y1 e Y2, são aplicadas como entradas da porta NOR que está presente no segundo nível. Então, a saída desta porta NOR é
$$Y={\left ( Y_{1}+Y_{2} \right )}'$$
Substituto $Y_{1}$ e $Y_{2}$ valores na equação acima.
$$Y={\left ( AB+CD \right )}'$$
Portanto, a saída desta realização da lógica AND-NOR é ${\left ( AB+CD \right )}'$. Esta função booleana está emAND-OR-InvertFormato. Uma vez que não podemos implementá-lo usando uma única porta lógica, esta realização lógica AND-NOR é umnon-degenerative form
Lógica OR-AND
Nesta realização lógica, as portas OR estão presentes no primeiro nível e as portas AND estão presentes no segundo nível. A figura a seguir mostra um exemplo paraOR-AND logic realização.

Anteriormente, obtivemos as saídas das portas lógicas de primeiro nível como $Y_{1}=A+B$ e $Y_{2}=C+D$.
Essas saídas, $Y_{1}$ e $Y_{2}$são aplicados como entradas da porta AND que está presente no segundo nível. Então, a saída desta porta AND é
$$Y=Y_{1}Y_{2}$$
Substituto $Y_{1}$ e $Y_{2}$ valores na equação acima.
$$Y = \left ( A+B \right )\left ( C+D \right )$$
Portanto, a saída desta realização da lógica OR-AND é (A + B) (C + D). Esta função booleana está emProduct of SumsFormato. Uma vez que não podemos implementá-lo usando uma única porta lógica, esta realização lógica OR-AND é umnon-degenerative form.
Da mesma forma, você pode verificar se as realizações restantes pertencem a esta categoria ou não.
Combinational circuitsconsistem em portas lógicas. Esses circuitos operam com valores binários. A (s) saída (s) do circuito combinacional depende da combinação das entradas presentes. A figura a seguir mostra oblock diagram de circuito combinacional.

Este circuito combinacional tem 'n' variáveis de entrada e 'm' saídas. Cada combinação de variáveis de entrada afetará a (s) saída (s).
Procedimento de projeto de circuitos combinacionais
Encontre o número necessário de variáveis de entrada e saídas de especificações dadas.
Formule o Truth table. Se houver 'n' variáveis de entrada, haverá 2n combinações possíveis. Para cada combinação de entrada, encontre os valores de saída.
Encontre o Boolean expressionspara cada saída. Se necessário, simplifique essas expressões.
Implemente as expressões booleanas acima correspondentes a cada saída usando Logic gates.
Conversores de Código
Discutimos vários códigos no capítulo códigos nomeados. Os conversores, que convertem um código em outro código, são chamados decode converters. Esses conversores de código consistem basicamente em portas lógicas.
Exemplo
Código binário para conversor de código Gray
Vamos implementar um conversor, que converte um código binário de 4 bits WXYZ em seu código Gray ABCD equivalente.
A tabela a seguir mostra o Truth table de um código binário de 4 bits para conversor de código Gray.
| Código binário WXYZ | WXYZ Gray código ABCD |
|---|---|
| 0000 | 0000 |
| 0001 | 0001 |
| 0010 | 0011 |
| 0011 | 0010 |
| 0100 | 0110 |
| 0101 | 0111 |
| 0110 | 0101 |
| 0111 | 0100 |
| 1000 | 1100 |
| 1001 | 1101 |
| 1010 | 1111 |
| 1011 | 1110 |
| 1100 | 1010 |
| 1101 | 1011 |
| 1110 | 1001 |
| 1111 | 1000 |
Na tabela da verdade, podemos escrever o Boolean functions para cada bit de saída do código Gray conforme abaixo.
$$A=\sum m\left (8,9,10,11,12,13,14,15 \right )$$
$$B=\sum m\left (4,5,6,7,8,9,10,11 \right )$$
$$C=\sum m\left (2,3,4,5,10,11,12,13 \right )$$
$$D=\sum m\left (1,2,5,6,9,10,13,14 \right )$$
Vamos simplificar as funções acima usando 4 K-Maps de variáveis.
A figura a seguir mostra o 4 variable K-Map para simplificar Boolean function, A.

Ao agrupar 8 adjacentes, obtivemos $A=W$.
A figura a seguir mostra o 4 variable K-Map para simplificar Boolean function, B.

Existem dois grupos de 4 adjacentes. Após o agrupamento, obteremos B como
$$B={W}'X+W{X}'=W\oplus X $$
Da mesma forma, obteremos as seguintes funções booleanas para C e D após a simplificação.
$$C={X}'Y+X{Y}'=X \oplus Y$$
$$D={Y}'Z+Y{Z}'=Y \oplus Z$$
A figura a seguir mostra o circuit diagram de código binário de 4 bits para conversor de código Gray.

Como as saídas dependem apenas das entradas presentes, este conversor de código binário para código Gray de 4 bits é um circuito combinacional. Da mesma forma, você pode implementar outros conversores de código.
Gerador de bits de paridade
Existem dois tipos de geradores de bit de paridade com base no tipo de bit de paridade que está sendo gerado. Even parity generatorgera um bit de paridade par. Similarmente,odd parity generator gera um bit de paridade ímpar.
Even Parity Generator
Agora, vamos implementar um gerador de paridade par para uma entrada binária de 3 bits, WXY. Ele gera um bit de paridade par, P. Se um número ímpar de uns estiver presente na entrada, então o bit de paridade par, P deve ser '1' para que a palavra resultante contenha um número par de uns. Para outras combinações de entrada, mesmo bit de paridade, P deve ser '0'. A tabela a seguir mostra oTruth table de gerador de paridade par.
| Entrada Binária WXY | Mesmo bit de paridade P |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 1 |
| 011 | 0 |
| 100 | 1 |
| 101 | 0 |
| 110 | 0 |
| 111 | 1 |
A partir da tabela da verdade acima, podemos escrever o Boolean function para bit de paridade par como
$$P={W}'{X}'Y+{W}'X{Y}'+W{X}'{Y}'+WXY$$
$\Rightarrow P={W}'\left ( {X}'Y+X{Y}' \right )+W\left ({X}'{Y}'+XY \right )$
$\Rightarrow P={W}'\left ( X \oplus Y \right )+W{\left (X \oplus Y \right )}'=W \oplus X \oplus Y$
A figura a seguir mostra o circuit diagram de gerador de paridade par.

Este circuito consiste em dois Exclusive-OR gatestendo duas entradas cada. A primeira porta OR exclusiva tem duas entradas W e X e produz uma saída W ⊕ X. Esta saída é fornecida como uma entrada da segunda porta OU exclusiva. A outra entrada dessa segunda porta OU Exclusiva é Y e produz uma saída de W ⊕ X ⊕ Y.
Gerador de paridade ímpar
Se um número par de uns estiver presente na entrada, então o bit de paridade ímpar P deve ser '1' para que a palavra resultante contenha um número ímpar de uns. Para outras combinações de entrada, bit de paridade ímpar, P deve ser '0'.
Siga o mesmo procedimento do gerador de paridade par para implementar o gerador de paridade ímpar. ocircuit diagram de gerador de paridade ímpar é mostrado na figura a seguir.

O diagrama de circuito acima consiste em porta Ex-OR no primeiro nível e porta Ex-NOR no segundo nível. Como a paridade ímpar é exatamente oposta à paridade par, podemos colocar um inversor na saída do gerador de paridade par. Nesse caso, o primeiro e o segundo níveis contêm uma porta ExOR em cada nível e o terceiro nível consiste em um inversor.
Verificador de Paridade
Existem dois tipos de verificadores de paridade com base no tipo de paridade que deve ser verificado. Even parity checkerverifica o erro nos dados transmitidos, que contém bits de mensagem junto com paridade par. Similarmente,odd parity checker verifica o erro nos dados transmitidos, que contém bits de mensagem junto com paridade ímpar.
Verificador de paridade uniforme
Agora, vamos implementar um circuito verificador de paridade par. Suponha uma entrada binária de 3 bits, WXY é transmitido junto com um bit de paridade par, P. Portanto, a palavra resultante (dados) contém 4 bits, que serão recebidos como a entrada do verificador de paridade par.
Isso gera um even parity check bit, E. Este bit será zero, se os dados recebidos contiverem um número par de uns. Isso significa que não há erro nos dados recebidos. Este bit de verificação de paridade par será um, se os dados recebidos contiverem um número ímpar de unidades. Isso significa que há um erro nos dados recebidos.
A tabela a seguir mostra o Truth table de um verificador de paridade par.
| Dados recebidos de 4 bits WXYP | Bit E de verificação de paridade uniforme |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 1 |
| 0011 | 0 |
| 0100 | 1 |
| 0101 | 0 |
| 0110 | 0 |
| 0111 | 1 |
| 1000 | 1 |
| 1001 | 0 |
| 1010 | 0 |
| 1011 | 1 |
| 1100 | 0 |
| 1101 | 1 |
| 1110 | 1 |
| 1111 | 0 |
Na tabela de verdade acima, podemos observar que o valor do bit de verificação de paridade par é '1', quando o número ímpar de uns está presente nos dados recebidos. Isso significa que a função booleana do bit de verificação de paridade par é umodd function. A função OR exclusivo satisfaz esta condição. Portanto, podemos escrever diretamente oBoolean function de bit de verificação de paridade par como
$$E=W \oplus X \oplus Y \oplus P$$
A figura a seguir mostra o circuit diagram de verificador de paridade par.

Este circuito consiste em três Exclusive-OR gatestendo duas entradas cada. Os portões de primeiro nível produzem saídas de$W \oplus X$ E $Y \oplus P$. O portão OU Exclusivo, que está no segundo nível, produz uma saída de$W \oplus X \oplus Y \oplus P$
Verificador de paridade ímpar
Suponha uma entrada binária de 3 bits, WXY é transmitido junto com o bit de paridade ímpar, P. Portanto, a palavra resultante (dados) contém 4 bits, que serão recebidos como a entrada do verificador de paridade ímpar.
Isso gera um odd parity check bit, E. Este bit será zero, se os dados recebidos contiverem um número ímpar de unidades. Isso significa que não há erro nos dados recebidos. Este bit de verificação de paridade ímpar será um, se os dados recebidos contiverem um número par de unidades. Isso significa que há um erro nos dados recebidos.
Siga o mesmo procedimento de um verificador de paridade par para implementar um verificador de paridade ímpar. ocircuit diagram do verificador de paridade ímpar é mostrado na figura a seguir.

O diagrama de circuito acima consiste em portas Ex-OR no primeiro nível e portas Ex-NOR no segundo nível. Uma vez que a paridade ímpar é exatamente oposta à paridade par, podemos colocar um inversor na saída do verificador de paridade par. Nesse caso, o primeiro, o segundo e o terceiro níveis contêm duas portas Ex-OR, uma porta Ex-OR e um inversor, respectivamente.
Somador Binário
A operação aritmética mais básica é a adição. O circuito, que realiza a adição de dois números binários, é conhecido comoBinary adder. Primeiro, vamos implementar um somador, que realiza a adição de dois bits.
Meio somador
Metade somador é um circuito combinacional, que realiza a adição de dois números binários A e B são de single bit. Ele produz a soma de duas saídas, S & carry, C.
o Truth table de meio somador é mostrado abaixo.
| Entradas | Saídas | ||
|---|---|---|---|
| UMA | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Quando fazemos a adição de dois bits, a soma resultante pode ter os valores variando de 0 a 2 em decimal. Podemos representar os dígitos decimais 0 e 1 com um único bit em binário. Mas, não podemos representar o dígito decimal 2 com um único bit em binário. Portanto, exigimos dois bits para representá-lo em binário.
Deixe, soma, S é o bit menos significativo e transporte, C é o bit mais significativo da soma resultante. Para as três primeiras combinações de entradas, carry, C é zero e o valor de S será zero ou um com base nonumber of onespresente nas entradas. Mas, para a última combinação de entradas, carry, C é um e sum, S é zero, já que a soma resultante é dois.
Da tabela da verdade, podemos escrever diretamente o Boolean functions para cada saída como
$$S=A \oplus B$$
$C=AB$
Podemos implementar as funções acima com porta Ex-OR de 2 entradas e porta AND de 2 entradas. ocircuit diagram de meio somador é mostrado na figura a seguir.

No circuito acima, uma porta Ex-OR de duas entradas e uma porta AND de duas entradas produzem soma, S & carry, C respectivamente. Portanto, o meio-somador realiza a adição de dois bits.
Full Adder
Full somador é um circuito combinacional, que realiza o addition of three bitsA, B e C em . Onde, A e B são os dois bits significativos paralelos e C in é o bit de transporte, que é gerado no estágio anterior. Este somador Full também produz soma de duas saídas, S & carry, C out , que são semelhantes a Half somador.
o Truth table do somador completo é mostrado abaixo.
| Entradas | Saídas | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Quando fazemos a adição de três bits, a soma resultante pode ter os valores variando de 0 a 3 em decimal. Podemos representar os dígitos decimais 0 e 1 com um único bit em binário. Mas, não podemos representar os dígitos decimais 2 e 3 com um único bit em binário. Portanto, exigimos dois bits para representar esses dois dígitos decimais em binário.
Deixe, sum, S é o bit menos significativo e carry, C out é o bit mais significativo da soma resultante. É fácil preencher os valores das saídas para todas as combinações de entradas na tabela verdade. Apenas conte onumber of onespresente nas entradas e escreva o número binário equivalente nas saídas. Se C in for igual a zero, a tabela verdade do somador completo é igual à tabela verdade do meio somador.
Iremos obter o seguinte Boolean functions para cada saída após a simplificação.
$$S=A \oplus B \oplus C_{in}$$
$c_{out} = AB + \left ( A \oplus B \right )c_{in}$
A soma, S é igual a um, quando o número ímpar de uns estiver presente nas entradas. Sabemos que a porta Ex-OR produz uma saída, que é uma função ímpar. Portanto, podemos usar duas portas Ex-OR de 2 entradas ou uma porta Ex-OR de 3 entradas para produzir a soma S. Podemos implementar o carry, C out usando duas portas AND de 2 entradas e uma porta OR. ocircuit diagram de somador completo é mostrado na figura a seguir.
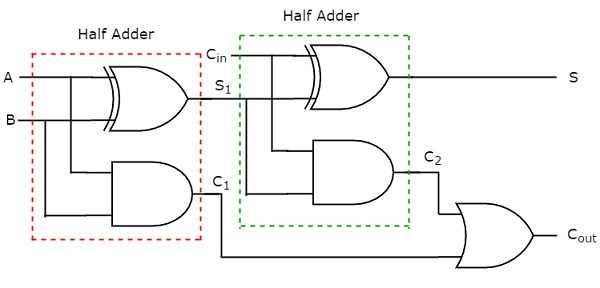
Este somador é chamado de Full adderporque para implementar um somador completo, exigimos dois meio somadores e uma porta OR. Se C in for zero, o somador completo se tornará meio somador. Podemos verificar isso facilmente no diagrama de circuito acima ou nas funções booleanas de saídas do somador completo.
Adicionador binário de 4 bits
O somador binário de 4 bits realiza o addition of two 4-bit numbers. Deixe os números binários de 4 bits,$A=A_{3}A_{2}A_{1}A_{0}$ e $B= B_{3}B_{2}B_{1}B_{0}$. Podemos implementar somador binário de 4 bits de uma das seguintes maneiras.
Use um meio somador para fazer a adição de dois bits menos significativos e três somadores completos para fazer a adição de três bits significativos mais altos.
Use quatro somadores completos para uniformidade. Como o carry inicial C in é zero, o somador completo que é usado para adicionar os bits menos significativos torna-se meio somador.
Por enquanto, consideramos a segunda abordagem. oblock diagram de somador binário de 4 bits é mostrado na figura a seguir.

Aqui, os 4 somadores completos são colocados em cascata. Cada somador Full está obtendo os respectivos bits de duas entradas paralelas A e B. A saída de transporte de um somador Completo será a entrada de transporte do somador Completo de ordem superior subsequente. Este somador binário de 4 bits produz a soma resultante com no máximo 5 bits. Então, a partir da última etapa, o somador completo será o MSB.
Desta forma, podemos implementar qualquer somador binário de ordem superior apenas colocando em cascata o número necessário de somadores completos. Este somador binário também é chamado deripple carry (binary) adder porque o transporte se propaga (ondula) de um estágio para o próximo.
Subtrator Binário
O circuito, que realiza a subtração de dois números binários é conhecido como Binary subtractor. Podemos implementar o subtrator binário seguindo dois métodos.
- Subtratores completos em cascata
- Método de complemento de 2
No primeiro método, obteremos um subtrator binário de n bits colocando 'n' subtratores completos em cascata. Portanto, primeiro você pode implementar meio subtrator e subtrator completo, semelhante a meio somador e somador completo. Então, você pode implementar um subtrator binário de n bits, cascateando 'n' subtratores completos. Portanto, teremos dois circuitos separados para adição e subtração binárias de dois números binários.
No segundo método, podemos usar o mesmo somador binário para subtrair dois números binários apenas fazendo algumas modificações na segunda entrada. Portanto, ocorre a operação de adição binária internamente, mas a saída é a subtração resultante.
Sabemos que a subtração de dois números binários A e B pode ser escrita como,
$$A-B = A+\left ( {2}'s \: compliment \: of \: B \right )$$
$\Rightarrow A-B = A+\left ( {1}'s \: compliment \: of \: B \right )+1$
Subtrator binário de 4 bits
O subtrator binário de 4 bits produz o subtraction of two 4-bit numbers. Deixe os números binários de 4 bits,$A=A_{3}A_{2}A_{1}A_{0}$ e $B= B_{3}B_{2}B_{1}B_{0}$. Internamente, a operação do subtrator binário de 4 bits é semelhante à do somador binário de 4 bits. Se os bits normais do número binário A, bits complementados do número binário B e transporte inicial (emprestar), C em como um, são aplicados ao somador binário de 4 bits, então ele se torna subtrator binário de 4 bits. oblock diagram de subtrator binário de 4 bits é mostrado na figura a seguir.

Este subtrator binário de 4 bits produz uma saída, que tem no máximo 5 bits. Se o número binário A for maior que o número binário B, então o MSB da saída é zero e os bits restantes mantêm a magnitude de AB. Se o número binário A for menor que o número binário B, então o MSB da saída é um. Portanto, pegue o complemento de 2 da saída para obter a magnitude de AB.
Dessa forma, podemos implementar qualquer subtrator binário de ordem superior, apenas colocando em cascata o número necessário de somadores completos com as modificações necessárias.
Adicionador / Subtrator Binário
O circuito, que pode ser usado para realizar a adição ou subtração de dois números binários a qualquer momento, é conhecido como Binary Adder / subtractor. Ambos, somador binário e subtrator binário contêm um conjunto de somadores completos, que são colocados em cascata. Os bits de entrada do número binário A são aplicados diretamente no somador binário e no subtrator binário.
Existem duas diferenças nas entradas de somadores completos que estão presentes no somador binário e no subtrator binário.
Os bits de entrada do número binário B são aplicados diretamente aos somadores completos no somador binário, enquanto os bits complementados do número binário B são aplicados aos somadores completos no subtrator binário.
O transporte inicial, C 0 = 0, é aplicado no somador binário de 4 bits, enquanto o transporte inicial (empréstimo), C 0 = 1, é aplicado no subtrator binário de 4 bits.
Nós sabemos que um 2-input Ex-OR gateproduz uma saída, que é a mesma da primeira entrada quando a outra entrada é zero. Da mesma forma, ele produz uma saída, que é um complemento da primeira entrada quando a outra entrada é uma.
Portanto, podemos aplicar os bits de entrada do número binário B às portas Ex-OR de 2 entradas. A outra entrada para todas essas portas Ex-OR é C 0 . Portanto, com base no valor de C 0 , as portas Ex-OR produzem os bits normais ou complementados do número binário B.
Adicionador / subtrator binário de 4 bits
O somador / subtrator binário de 4 bits produz a adição ou a subtração de dois números de 4 bits com base no valor de transporte ou empréstimo inicial, 0 . Deixe os números binários de 4 bits,$A=A_{3}A_{2}A_{1}A_{0}$ e $B= B_{3}B_{2}B_{1}B_{0}$. A operação do somador / subtrator binário de 4 bits é semelhante à do somador / subtrator binário de 4 bits e do subtrator binário de 4 bits.
Aplique os bits normais dos números binários A e B e carregue ou tome emprestado, C 0 de externamente para um somador binário de 4 bits. oblock diagram de somador / subtrator binário de 4 bits é mostrado na figura a seguir.
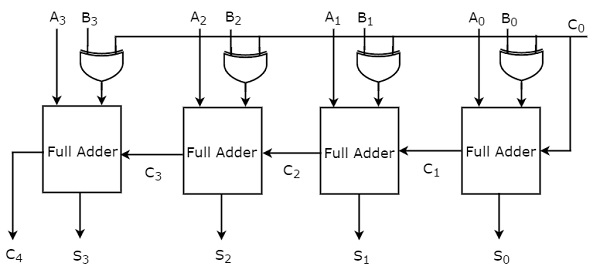
Se o carry inicial, 0 é zero, cada somador completo obtém os bits normais dos números binários A e B. Assim, o somador / subtrator binário de 4 bits produz uma saída, que é oaddition of two binary numbers A e B.
Se empréstimo inicial, 0 é um, então cada somador completo obtém os bits normais do número binário A e bits complementados do número binário B. Assim, o somador / subtrator binário de 4 bits produz uma saída, que é osubtraction of two binary numbers A e B.
Portanto, com a ajuda de portas Ex-OR adicionais, o mesmo circuito pode ser usado para adição e subtração de dois números binários.
Decoderé um circuito combinacional que possui 'n' linhas de entrada e no máximo 2 n linhas de saída. Uma dessas saídas estará ativa High com base na combinação de entradas presentes, quando o decodificador é habilitado. Isso significa que o decodificador detecta um código específico. As saídas do decodificador nada mais são do quemin terms de 'n' variáveis de entrada (linhas), quando está habilitado.
2 a 4 decodificador
Seja o decodificador 2 a 4 com duas entradas A 1 e A 0 e quatro saídas Y 3 , Y 2 , Y 1 e Y 0 . oblock diagram de 2 a 4 decodificadores é mostrado na figura a seguir.

Uma dessas quatro saídas será '1' para cada combinação de entradas quando habilitada, E será '1'. oTruth table de 2 a 4 decodificadores é mostrado abaixo.
| Habilitar | Entradas | Saídas | ||||
|---|---|---|---|---|---|---|
| E | A1 | A0 | Y3 | Y2 | Y1 | Y0 |
| 0 | x | x | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Na tabela da verdade, podemos escrever o Boolean functions para cada saída como
$$Y_{3}=E.A_{1}.A_{0}$$
$$ Y_{2}=E.A_{1}.{A_{0}}'$$
$$ Y_{1}=E.{A_{1}}'.A_{0}$$
$$ Y_{0}=E.{A_{1}}'.{A_{0}}'$$
Cada saída tem um termo de produto. Portanto, existem quatro termos de produto no total. Podemos implementar esses quatro termos de produto usando quatro portas AND com três entradas cada e dois inversores. ocircuit diagram de 2 a 4 decodificadores é mostrado na figura a seguir.

Portanto, as saídas de 2 a 4 decodificadores nada mais são do que min termsde duas variáveis de entrada A 1 e A 0 , quando habilitadas, E é igual a um. Se habilitado, E é zero, então todas as saídas do decodificador serão iguais a zero.
Da mesma forma, o decodificador 3 a 8 produz oito termos min de três variáveis de entrada A 2 , A 1 e A 0 e o decodificador 4 a 16 produz dezesseis termos min de quatro variáveis de entrada A 3 , A 2 , A 1 e A 0 .
Implementação de decodificadores de ordem superior
Agora, vamos implementar os dois decodificadores de ordem superior a seguir usando decodificadores de ordem inferior.
- 3 a 8 decodificador
- 4 a 16 decodificador
3 a 8 decodificador
Nesta seção, vamos implementar 3 to 8 decoder using 2 to 4 decoders. Sabemos que o decodificador 2 a 4 tem duas entradas, A 1 e A 0 e quatro saídas, Y 3 a Y 0 . Considerando que, o decodificador 3 a 8 tem três entradas A 2 , A 1 e A 0 e oito saídas, Y 7 a Y 0 .
Podemos encontrar o número de decodificadores de ordem inferior necessários para implementar o decodificador de ordem superior usando a seguinte fórmula.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
Onde,
$m_{1}$ é o número de saídas do decodificador de ordem inferior.
$m_{2}$ é o número de saídas do decodificador de ordem superior.
Aqui, $m_{1}$ = 4 e $m_{2}$ = 8. Substitua, esses dois valores na fórmula acima.
$$Required \: number \: of \: 2 \: to \: 4 \: decoders=\frac{8}{4}=2$$
Portanto, exigimos dois decodificadores de 2 a 4 para implementar um decodificador de 3 a 8. oblock diagram de 3 a 8 decodificadores usando 2 a 4 decodificadores é mostrado na figura a seguir.

As entradas paralelas A 1 e A 0 são aplicadas a cada 2 a 4 decodificadores. O complemento da entrada A 2 é conectado a Habilitar, E do decodificador 2 a 4 inferior para obter as saídas, Y 3 a Y 0 . Estes são oslower four min terms. A entrada, A 2, é conectada diretamente a Habilitar, E do decodificador 2 a 4 superiores para obter as saídas, Y 7 a Y 4 . Estes são oshigher four min terms.
4 a 16 decodificador
Nesta seção, vamos implementar 4 to 16 decoder using 3 to 8 decoders. Sabemos que o decodificador 3 a 8 tem três entradas A 2 , A 1 e A 0 e oito saídas, Y 7 a Y 0 . Considerando que, o decodificador 4 a 16 tem quatro entradas A 3 , A 2 , A 1 e A 0 e dezesseis saídas, Y 15 a Y 0
Conhecemos a seguinte fórmula para encontrar o número de decodificadores de ordem inferior necessários.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
Substituto, $m_{1}$ = 8 e $m_{2}$ = 16 na fórmula acima.
$$Required \: number \: of \: 3 \: to \: 8 decoders=\frac{16}{8}=2$$
Portanto, exigimos dois decodificadores de 3 a 8 para implementar um decodificador de 4 a 16. oblock diagram de 4 a 16 decodificadores usando 3 a 8 decodificadores é mostrado na figura a seguir.

As entradas paralelas A 2 , A 1 e A 0 são aplicadas a cada 3 a 8 decodificadores. O complemento da entrada, A3 é conectado a Habilitar, E do decodificador inferior de 3 a 8 para obter as saídas, Y 7 a Y 0 . Estes são oslower eight min terms. A entrada, A 3, é diretamente conectada a Ativar, E do decodificador superior 3 a 8 para obter as saídas, Y 15 a Y 8 . Estes são oshigher eight min terms.
A Encoderé um circuito combinacional que realiza a operação reversa do decodificador. Possui no máximo 2 n linhas de entrada e 'n' linhas de saída. Ele produzirá um código binário equivalente à entrada, que está ativa em Alta. Portanto, o codificador codifica 2 n linhas de entrada com 'n' bits. É opcional representar o sinal de habilitação em codificadores.
4 para 2 codificador
Seja 4 para 2 o codificador tem quatro entradas Y 3 , Y 2 , Y 1 e Y 0 e duas saídas A 1 e A 0 . oblock diagram de 4 a 2 Codificador é mostrado na figura a seguir.

A qualquer momento, apenas uma dessas 4 entradas pode ser '1' para obter o respectivo código binário na saída. oTruth table de 4 a 2 codificador é mostrado abaixo.
| Entradas | Saídas | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Na tabela da verdade, podemos escrever o Boolean functions para cada saída como
$$A_{1}=Y_{3}+Y_{2}$$
$$A_{0}=Y_{3}+Y_{1}$$
Podemos implementar as duas funções booleanas acima usando duas portas OR de entrada. ocircuit diagram de 4 a 2 codificadores é mostrado na figura a seguir.

O diagrama de circuito acima contém duas portas OR. Essas portas OR codificam as quatro entradas com dois bits
Octal para codificador binário
O codificador octal para binário tem oito entradas, Y 7 a Y 0 e três saídas A 2 , A 1 e A 0 . Codificador octal para binário nada mais é do que codificador 8 para 3. oblock diagram de octal para codificador binário é mostrado na figura a seguir.
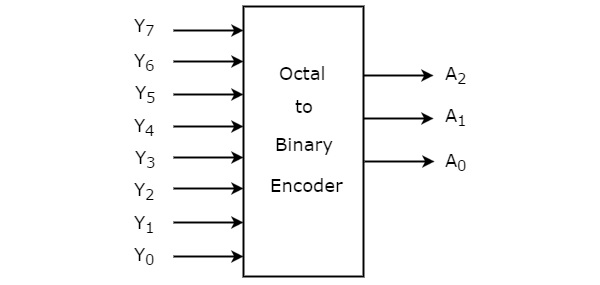
A qualquer momento, apenas uma dessas oito entradas pode ser '1' para obter o respectivo código binário. oTruth table de octal para codificador binário é mostrado abaixo.
| Entradas | Saídas | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Na tabela da verdade, podemos escrever o Boolean functions para cada saída como
$$A_{2}=Y_{7}+Y_{6}+Y_{5}+Y_{4}$$
$$A_{1}=Y_{7}+Y_{6}+Y_{3}+Y_{2}$$
$$A_{0}=Y_{7}+Y_{5}+Y_{3}+Y_{1}$$
Podemos implementar as funções booleanas acima usando quatro portas OR de entrada. ocircuit diagram de octal para codificador binário é mostrado na figura a seguir.

O diagrama de circuito acima contém três portas OR de 4 entradas. Essas portas OR codificam as oito entradas com três bits.
Desvantagens do codificador
A seguir estão as desvantagens do codificador normal.
Existe uma ambigüidade, quando todas as saídas do codificador são iguais a zero. Porque, poderia ser o código correspondente às entradas, quando apenas a entrada menos significativa é uma ou quando todas as entradas são zero.
Se mais de uma entrada estiver ativa em alta, o codificador produz uma saída, que pode não ser o código correto. Paraexample, se Y 3 e Y 6 forem '1', o codificador produzirá 111 na saída. Este não é um código equivalente correspondente a Y 3 , quando é '1', nem o código equivalente correspondente a Y 6 , quando é '1'.
Portanto, para superar essas dificuldades, devemos atribuir prioridades a cada entrada do codificador. Então, a saída do codificador será o código (binário) correspondente à (s) entrada (s) Alta (s) ativa (s), que tem maior prioridade. Este codificador é chamado depriority encoder.
Codificador de prioridade
Um codificador de prioridade 4 a 2 tem quatro entradas Y 3 , Y 2 , Y 1 e Y 0 e duas saídas A 1 e A 0 . Aqui, a entrada Y 3 tem a prioridade mais alta, enquanto a entrada Y 0 tem a prioridade mais baixa. Neste caso, mesmo se mais de uma entrada for '1' ao mesmo tempo, a saída será o código (binário) correspondente à entrada, que está tendohigher priority.
Nós consideramos mais um output, V para saber se o código disponível nas saídas é válido ou não.
Se pelo menos uma entrada do codificador for '1', então o código disponível nas saídas é válido. Nesse caso, a saída, V será igual a 1.
Se todas as entradas do codificador são '0', então o código disponível nas saídas não é válido. Nesse caso, a saída V será igual a 0.
o Truth table de 4 a 2 codificadores de prioridade é mostrado abaixo.
| Entradas | Saídas | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | x | 0 | 1 | 1 |
| 0 | 1 | x | x | 1 | 0 | 1 |
| 1 | x | x | x | 1 | 1 | 1 |
Usar 4 variable K-maps para obter expressões simplificadas para cada saída.
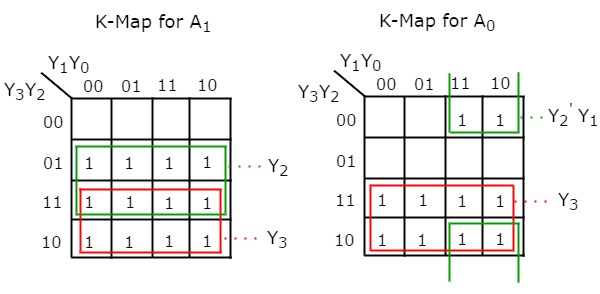
O simplificado Boolean functions está
$$A_{1}=Y_{3}+Y_{2}$$
$A_{0}=Y_{3}+{Y_{2}}'Y_{1}$
Da mesma forma, obteremos a função booleana de saída, V como
$$V=Y_{3}+Y_{2}+Y_{1}+Y_{0}$$
Podemos implementar as funções booleanas acima usando portas lógicas. ocircuit diagram de 4 a 2 codificadores de prioridade é mostrado na figura a seguir.

O diagrama de circuito acima contém duas portas OU de 2 entradas, uma porta OU de 4 entradas, uma porta E de 2 entradas e um inversor. Aqui, a combinação de porta e inversor AND é usada para produzir um código válido nas saídas, mesmo quando várias entradas são iguais a '1' ao mesmo tempo. Portanto, este circuito codifica as quatro entradas com dois bits com base nopriority atribuído a cada entrada.
Multiplexeré um circuito combinacional que tem no máximo 2 n entradas de dados, 'n' linhas de seleção e linha de saída única. Uma dessas entradas de dados será conectada à saída com base nos valores das linhas de seleção.
Como há 'n' linhas de seleção, haverá 2 n combinações possíveis de zeros e uns. Portanto, cada combinação selecionará apenas uma entrada de dados. Multiplexer também é chamado deMux.
Multiplexador 4x1
O Multiplexador 4x1 tem quatro entradas de dados I 3 , I 2 , I 1 e I 0 , duas linhas de seleção s 1 & s 0 e uma saída Y.block diagram de 4x1 Multiplexer é mostrado na figura a seguir.

Uma dessas 4 entradas será conectada à saída com base na combinação de entradas presentes nessas duas linhas de seleção. Truth table de 4x1 Multiplexer é mostrado abaixo.
| Linhas de Seleção | Resultado | |
|---|---|---|
| S1 | S0 | Y |
| 0 | 0 | I 0 |
| 0 | 1 | Eu 1 |
| 1 | 0 | I 2 |
| 1 | 1 | I 3 |
Da tabela da verdade, podemos escrever diretamente o Boolean function para saída, Y como
$$Y={S_{1}}'{S_{0}}'I_{0}+{S_{1}}'S_{0}I_{1}+S_{1}{S_{0}}'I_{2}+S_{1}S_{0}I_{3}$$
Podemos implementar esta função booleana usando inversores, portas AND e porta OR. ocircuit diagram de multiplexador 4x1 é mostrado na figura a seguir.

Podemos compreender facilmente o funcionamento do circuito acima. Da mesma forma, você pode implementar o multiplexador 8x1 e o multiplexador 16x1 seguindo o mesmo procedimento.
Implementação de multiplexadores de ordem superior.
Agora, vamos implementar os dois multiplexadores de ordem superior a seguir usando Multiplexadores de ordem inferior.
- Multiplexer 8x1
- Multiplexer 16x1
Multiplexer 8x1
Nesta seção, vamos implementar o Multiplexador 8x1 usando Multiplexadores 4x1 e Multiplexador 2x1. Sabemos que o Multiplexador 4x1 possui 4 entradas de dados, 2 linhas de seleção e uma saída. Enquanto o Multiplexador 8x1 possui 8 entradas de dados, 3 linhas de seleção e uma saída.
Então, nós exigimos dois 4x1 Multiplexersna primeira fase, a fim de obter as 8 entradas de dados. Uma vez que cada multiplexador 4x1 produz uma saída, exigimos um2x1 Multiplexer na segunda fase, considerando as saídas da primeira fase como entradas e para produzir a saída final.
Deixe que o Multiplexador 8x1 tenha oito entradas de dados I 7 a I 0 , três linhas de seleção s 2 , s 1 e s0 e uma saída Y.Truth table de 8x1 Multiplexer é mostrado abaixo.
| Entradas de seleção | Resultado | ||
|---|---|---|---|
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | I 0 |
| 0 | 0 | 1 | Eu 1 |
| 0 | 1 | 0 | I 2 |
| 0 | 1 | 1 | I 3 |
| 1 | 0 | 0 | I 4 |
| 1 | 0 | 1 | I 5 |
| 1 | 1 | 0 | I 6 |
| 1 | 1 | 1 | I 7 |
Podemos implementar o Multiplexador 8x1 usando multiplexadores de ordem inferior facilmente, considerando a tabela da verdade acima. oblock diagram de 8x1 Multiplexer é mostrado na figura a seguir.

O mesmo selection lines, s1 & s0são aplicados a ambos os Multiplexadores 4x1. As entradas de dados do Multiplexador 4x1 superior são I 7 a I 4 e as entradas de dados do Multiplexador 4x1 inferior são I 3 a I 0 . Portanto, cada Multiplexador 4x1 produz uma saída com base nos valores das linhas de seleção, s 1 e s 0 .
As saídas dos Multiplexadores 4x1 do primeiro estágio são aplicadas como entradas do Multiplexador 2x1 que está presente no segundo estágio. O outroselection line, s2 é aplicado ao Multiplexador 2x1.
Se s 2 for zero, a saída do Multiplexador 2x1 será uma das 4 entradas I 3 a I 0 com base nos valores das linhas de seleção s 1 e s 0 .
Se s 2 for um, então a saída do Multiplexador 2x1 será uma das 4 entradas I 7 a I 4 com base nos valores das linhas de seleção s 1 e s 0 .
Portanto, a combinação geral de dois Multiplexadores 4x1 e um Multiplexador 2x1 funciona como um Multiplexador 8x1.
Multiplexer 16x1
Nesta seção, vamos implementar o Multiplexador 16x1 usando Multiplexadores 8x1 e Multiplexador 2x1. Sabemos que o Multiplexador 8x1 possui 8 entradas de dados, 3 linhas de seleção e uma saída. Enquanto o Multiplexador 16x1 possui 16 entradas de dados, 4 linhas de seleção e uma saída.
Então, nós exigimos dois 8x1 Multiplexersna primeira fase, a fim de obter as 16 entradas de dados. Visto que cada Multiplexador 8x1 produz uma saída, exigimos um Multiplexador 2x1 no segundo estágio, considerando as saídas do primeiro estágio como entradas e para produzir a saída final.
Deixe que o Multiplexador 16x1 tenha dezesseis entradas de dados I 15 a I 0 , quatro linhas de seleção s 3 a s 0 e uma saída Y.Truth table de 16x1 Multiplexer é mostrado abaixo.
| Entradas de seleção | Resultado | |||
|---|---|---|---|---|
| S3 | S2 | S1 | S0 | Y |
| 0 | 0 | 0 | 0 | I 0 |
| 0 | 0 | 0 | 1 | Eu 1 |
| 0 | 0 | 1 | 0 | I 2 |
| 0 | 0 | 1 | 1 | I 3 |
| 0 | 1 | 0 | 0 | I 4 |
| 0 | 1 | 0 | 1 | I 5 |
| 0 | 1 | 1 | 0 | I 6 |
| 0 | 1 | 1 | 1 | I 7 |
| 1 | 0 | 0 | 0 | I 8 |
| 1 | 0 | 0 | 1 | I 9 |
| 1 | 0 | 1 | 0 | I 10 |
| 1 | 0 | 1 | 1 | I 11 |
| 1 | 1 | 0 | 0 | I 12 |
| 1 | 1 | 0 | 1 | I 13 |
| 1 | 1 | 1 | 0 | I 14 |
| 1 | 1 | 1 | 1 | I 15 |
Podemos implementar o Multiplexador 16x1 usando Multiplexadores de ordem inferior facilmente, considerando a tabela da verdade acima. oblock diagram do Multiplexer 16x1 é mostrado na figura a seguir.

o same selection lines, s2, s1 & s0são aplicados a ambos os Multiplexadores 8x1. As entradas de dados do Multiplexador 8x1 superior são I 15 a I 8 e as entradas de dados do Multiplexador 8x1 inferior são I 7 a I 0 . Portanto, cada Multiplexador 8x1 produz uma saída com base nos valores das linhas de seleção, s 2 , s 1 e s 0 .
As saídas dos Multiplexadores 8x1 do primeiro estágio são aplicadas como entradas do Multiplexador 2x1 que está presente no segundo estágio. O outroselection line, s3 é aplicado ao Multiplexador 2x1.
Se s 3 for zero, a saída do Multiplexador 2x1 será uma das 8 entradas Is 7 a I 0 com base nos valores das linhas de seleção s 2 , s 1 e s 0 .
Se s 3 for um, então a saída do Multiplexador 2x1 será uma das 8 entradas I 15 a I 8 com base nos valores das linhas de seleção s 2 , s 1 e s 0 .
Portanto, a combinação geral de dois Multiplexadores 8x1 e um Multiplexador 2x1 funciona como um Multiplexador 16x1.
De-Multiplexeré um circuito combinacional que realiza a operação reversa do Multiplexer. Possui entrada única, 'n' linhas de seleção e máximo de 2 n saídas. A entrada será conectada a uma dessas saídas com base nos valores das linhas de seleção.
Como há 'n' linhas de seleção, haverá 2 n combinações possíveis de zeros e uns. Portanto, cada combinação pode selecionar apenas uma saída. De-Multiplexer também é chamado deDe-Mux.
1x4 De-Multiplexer
1x4 De-Multiplexer tem uma entrada I, duas linhas de seleção, s 1 e s 0 e quatro saídas Y 3 , Y 2 , Y 1 e Y 0 . oblock diagram de 1x4 De-Multiplexer é mostrado na figura a seguir.

A única entrada 'I' será conectada a uma das quatro saídas, Y 3 a Y 0, com base nos valores das linhas de seleção s 1 e s0. oTruth table de 1x4 De-Multiplexer é mostrado abaixo.
| Entradas de seleção | Saídas | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
A partir da tabela de verdade acima, podemos escrever diretamente o Boolean functions para cada saída como
$$Y_{3}=s_{1}s_{0}I$$
$$Y_{2}=s_{1}{s_{0}}'I$$
$$Y_{1}={s_{1}}'s_{0}I$$
$$Y_{0}={s_1}'{s_{0}}'I$$
Podemos implementar essas funções booleanas usando inversores e portas AND de 3 entradas. ocircuit diagram de 1x4 De-Multiplexer é mostrado na figura a seguir.

Podemos compreender facilmente o funcionamento do circuito acima. Da mesma forma, você pode implementar 1x8 De-Multiplexer e 1x16 De-Multiplexer seguindo o mesmo procedimento.
Implementação de De-Multiplexers de ordem superior
Agora, vamos implementar os seguintes dois De-Multiplexers de ordem superior usando De-Multiplexers de ordem inferior.
- 1x8 De-Multiplexer
- 1x16 De-Multiplexer
1x8 De-Multiplexer
Nesta seção, vamos implementar 1x8 De-Multiplexer usando 1x4 De-Multiplexer e 1x2 De-Multiplexer. Sabemos que 1x4 De-Multiplexer tem uma única entrada, duas linhas de seleção e quatro saídas. Considerando que, 1x8 De-Multiplexer tem uma única entrada, três linhas de seleção e oito saídas.
Então, nós exigimos dois 1x4 De-Multiplexersna segunda fase, a fim de obter os oito resultados finais. Como o número de entradas no segundo estágio é dois, exigimos1x2 DeMultiplexerno primeiro estágio, de modo que as saídas do primeiro estágio sejam as entradas do segundo estágio. A entrada deste De-Multiplexer 1x2 será a entrada geral do De-Multiplexer 1x8.
Deixe que o De-Multiplexer 1x8 tenha uma entrada I, três linhas de seleção s 2 , s 1 e s 0 e as saídas Y 7 a Y 0 . oTruth table de 1x8 De-Multiplexer é mostrado abaixo.
| Entradas de seleção | Saídas | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Podemos implementar 1x8 De-Multiplexer usando Multiplexers de ordem inferior facilmente, considerando a tabela de verdade acima. oblock diagram de 1x8 De-Multiplexer é mostrado na figura a seguir.

O comum selection lines, s1 & s0são aplicados a ambos os De-Multiplexers 1x4. As saídas do De-Multiplexer 1x4 superior são Y 7 a Y 4 e as saídas do De-Multiplexer 1x4 inferior são Y 3 a Y 0 .
O outro selection line, s2é aplicado a 1x2 De-Multiplexer. Se s 2 for zero, então uma das quatro saídas do De-Multiplexer 1x4 inferior será igual à entrada, I com base nos valores das linhas de seleção s 1 e s 0 . Da mesma forma, se s 2 for um, então uma das quatro saídas do DeMultiplexador 1x4 superior será igual à entrada, I com base nos valores das linhas de seleção s 1 e s 0 .
1x16 De-Multiplexer
Nesta seção, vamos implementar 1x16 De-Multiplexer usando 1x8 De-Multiplexer e 1x2 De-Multiplexer. Sabemos que 1x8 De-Multiplexer tem uma única entrada, três linhas de seleção e oito saídas. Considerando que, 1x16 De-Multiplexer tem uma única entrada, quatro linhas de seleção e dezesseis saídas.
Então, nós exigimos dois 1x8 De-Multiplexersna segunda fase, a fim de obter os dezesseis resultados finais. Como o número de entradas no segundo estágio é dois, exigimos1x2 DeMultiplexerno primeiro estágio, de modo que as saídas do primeiro estágio sejam as entradas do segundo estágio. A entrada deste De-Multiplexer 1x2 será a entrada geral do De-Multiplexer 1x16.
Deixe que o De-Multiplexer 1x16 tenha uma entrada I, quatro linhas de seleção s 3 , s 2 , s 1 & s 0 e saídas Y 15 a Y 0 . oblock diagram de 1x16 De-Multiplexer usando Multiplexers de ordem inferior é mostrado na figura a seguir.
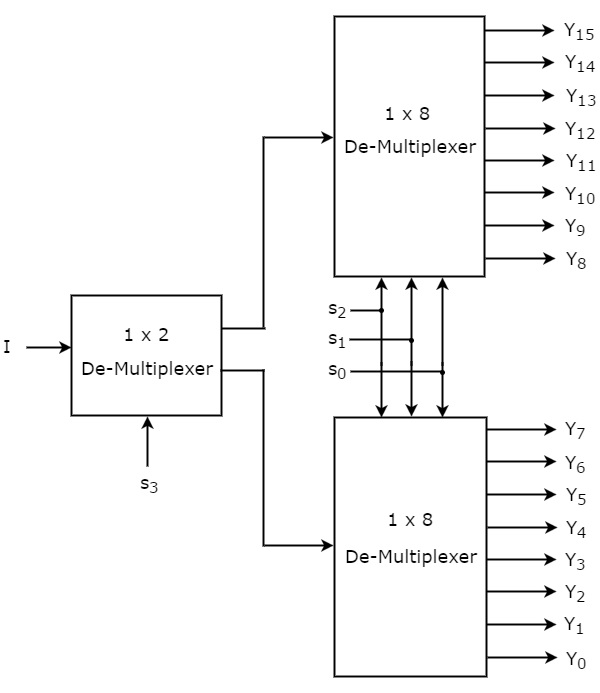
O comum selection lines s2, s1 & s0são aplicados a ambos 1x8 De-Multiplexers. As saídas do DeMultiplexador 1x8 superior são Y 15 a Y 8 e as saídas do DeMultiplexador 1x8 inferior são Y 7 a Y 0 .
O outro selection line, s3é aplicado a 1x2 De-Multiplexer. Se s 3 for zero, então uma das oito saídas do De-Multiplexer 1x8 inferior será igual à entrada, I com base nos valores das linhas de seleção s 2 , s 1 e s 0 . Da mesma forma, se s3 for um, então uma das 8 saídas do De-Multiplexer 1x8 superior será igual à entrada, I com base nos valores das linhas de seleção s 2 , s 1 & s 0 .
Dispositivos Lógicos Programáveis (PLDs)são os circuitos integrados. Eles contêm uma matriz de portas AND e outra matriz de portas OR. Existem três tipos de PLDs com base no tipo de matriz (s), que possui recurso programável.
- Memória somente leitura programável
- Lógica de matriz programável
- Matriz Lógica Programável
O processo de inserir as informações nesses dispositivos é conhecido como programming. Basicamente, os usuários podem programar esses dispositivos ou ICs eletricamente para implementar as funções booleanas com base no requisito. Aqui, o termo programação refere-se à programação de hardware, mas não à programação de software.
Memória programável somente leitura (PROM)
A memória somente leitura (ROM) é um dispositivo de memória que armazena as informações binárias permanentemente. Isso significa que não podemos alterar essas informações armazenadas de forma alguma posteriormente. Se a ROM tem recurso programável, é chamado deProgrammable ROM (PROM). O usuário tem a flexibilidade de programar as informações binárias eletricamente uma vez usando o programador PROM.
PROM é um dispositivo lógico programável que possui matriz AND fixa e matriz OR programável. oblock diagram de PROM é mostrado na figura a seguir.

Aqui, as entradas das portas AND não são do tipo programável. Portanto, temos que gerar 2 n termos de produto usando 2 n portas AND com n entradas cada. Podemos implementar esses termos de produto usando o decodificador nx2 n . Então, este decodificador gera 'n'min terms.
Aqui, as entradas das portas OR são programáveis. Isso significa que podemos programar qualquer número de termos de produto necessários, uma vez que todas as saídas das portas AND são aplicadas como entradas para cada porta OR. Portanto, os resultados do PROM serão na forma desum of min terms.
Exemplo
Vamos implementar o seguinte Boolean functions usando PROM.
$$A(X,Y,Z)=\sum m\left ( 5,6,7 \right )$$
$$B(X,Y,Z)=\sum m\left ( 3,5,6,7 \right )$$
As duas funções fornecidas estão na forma de termos mínimos e cada função tem três variáveis X, Y e Z. Portanto, exigimos um decodificador de 3 a 8 e duas portas OR programáveis para produzir essas duas funções. O correspondentePROM é mostrado na figura a seguir.

Aqui, o decodificador de 3 a 8 gera oito termos min. As duas portas OR programáveis têm acesso a todos esses termos mínimos. Porém, apenas os termos mínimos exigidos são programados para produzir as respectivas funções booleanas por cada porta OR. O símbolo 'X' é usado para conexões programáveis.
Lógica de matriz programável (PAL)
PAL é um dispositivo lógico programável que possui matriz AND programável e matriz OR fixa. A vantagem do PAL é que podemos gerar apenas os termos de produto necessários da função booleana, em vez de gerar todos os termos mínimos usando portas AND programáveis. oblock diagram de PAL é mostrado na figura a seguir.

Aqui, as entradas das portas AND são programáveis. Isso significa que cada porta AND tem entradas normais e complementadas de variáveis. Portanto, com base no requisito, podemos programar qualquer uma dessas entradas. Portanto, podemos gerar apenas o necessárioproduct terms usando essas portas AND.
Aqui, as entradas das portas OR não são do tipo programável. Portanto, o número de entradas para cada porta OR será do tipo fixo. Portanto, aplique os termos de produto necessários a cada porta OU como entradas. Portanto, as saídas do PAL serão na forma desum of products form.
Exemplo
Vamos implementar o seguinte Boolean functions usando PAL.
$$A=XY+X{Z}'$$
$$A=X{Y}'+Y{Z}'$$
As duas funções fornecidas estão na forma de soma de produtos. Existem dois termos de produto presentes em cada função booleana. Portanto, precisamos de quatro portas AND programáveis e duas portas OR fixas para produzir essas duas funções. O correspondentePAL é mostrado na figura a seguir.

o programmable AND gatestêm acesso às entradas normais e complementadas das variáveis. Na figura acima, as entradas X,${X}'$, Y, ${Y}'$, Z & ${Z}'$, estão disponíveis nas entradas de cada porta AND. Portanto, programe apenas os literais necessários para gerar um termo de produto para cada porta AND. O símbolo 'X' é usado para conexões programáveis.
Aqui, as entradas das portas OR são do tipo fixo. Assim, os termos do produto necessários estão conectados às entradas de cadaOR gate. Para que as portas OR produzam as respectivas funções booleanas. O símbolo '.' é usado para conexões fixas.
Matriz Lógica Programável (PLA)
O PLA é um dispositivo lógico programável que possui array AND programável e array OR programável. Portanto, é o PLD mais flexível. oblock diagram de PLA é mostrado na figura a seguir.

Aqui, as entradas das portas AND são programáveis. Isso significa que cada porta AND tem entradas normais e complementadas de variáveis. Portanto, com base no requisito, podemos programar qualquer uma dessas entradas. Portanto, podemos gerar apenas o necessárioproduct terms usando essas portas AND.
Aqui, as entradas das portas OR também são programáveis. Portanto, podemos programar qualquer número de termos de produto necessários, uma vez que todas as saídas das portas AND são aplicadas como entradas para cada porta OR. Portanto, as saídas do PAL serão na forma desum of products form.
Exemplo
Vamos implementar o seguinte Boolean functions usando PLA.
$$A=XY+X{Z}'$$
$$B=X{Y}'+YZ+X{Z}'$$
As duas funções fornecidas estão na forma de soma de produtos. O número de termos de produto presentes nas funções booleanas A e B fornecidas são dois e três, respectivamente. Um termo de produto,${Z}'X$ é comum em cada função.
Portanto, precisamos de quatro portas AND programáveis e duas portas OR programáveis para produzir essas duas funções. O correspondentePLA é mostrado na figura a seguir.
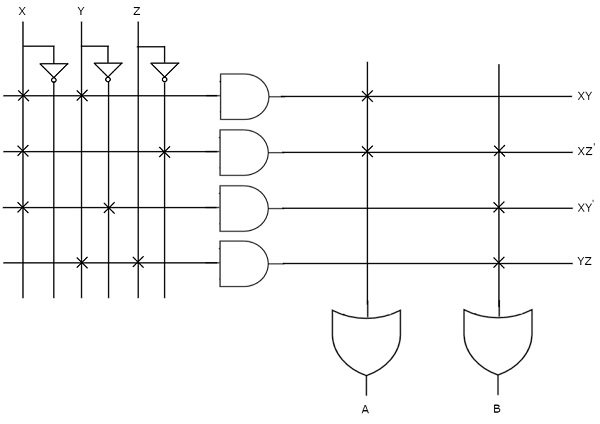
o programmable AND gatestêm acesso às entradas normais e complementadas das variáveis. Na figura acima, as entradas X,${X}'$, Y, ${Y}'$, Z & ${Z}'$, estão disponíveis nas entradas de cada porta AND. Portanto, programe apenas os literais necessários para gerar um termo de produto para cada porta AND.
Todos esses termos do produto estão disponíveis nas entradas de cada programmable OR gate. Porém, programe apenas os termos do produto necessários para produzir as respectivas funções booleanas por cada porta OR. O símbolo 'X' é usado para conexões programáveis.
Nos capítulos anteriores, implementamos vários circuitos combinacionais usando portas lógicas. Exceto a porta NOT, todas as portas lógicas restantes têm pelo menos duas entradas e uma única saída. Da mesma forma, othreshold gate também contém pelo menos uma entrada e apenas uma saída.
Além disso, ele contém os respectivos pesos para cada entrada e um valor limite. Os valores desses pesos e limiares podem ser de qualquer número real finito.
Noções básicas de porta de limiar
Sejam as entradas da porta de limiar X 1 , X 2 , X 3 ,…, X n . Os pesos correspondentes dessas entradas são W 1 , W 2 , W 3 ,…, W n . osymbol de Threshold gate é mostrado na figura a seguir.
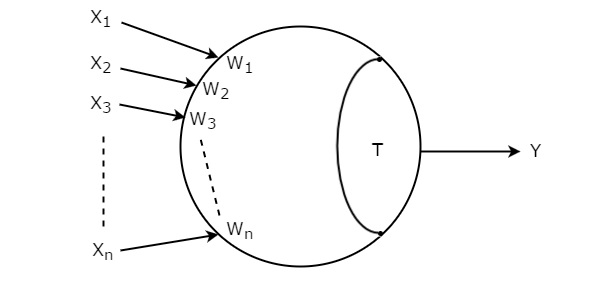
Threshold gateé representado por um círculo e tem 'n' entradas, X 1 a X n e uma única saída, Y. Este círculo é dividido em duas partes. Uma parte representa os pesos correspondentes às entradas e outra parte representa o valor limite, T.
A soma dos produtos dos insumos com pesos correspondentes é conhecida como weighted sum. Se esta soma ponderada for maior ou igual ao valor do Limiar, T, então apenas a saída Y será igual a um. Caso contrário, a saída, Y será igual a zero.
Mathematically, podemos escrever essa relação entre as entradas e a saída da porta de limiar como abaixo.
$$Y=1, if \: \: W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}+...W_{n}X_{n}\geq T$$
= 0, caso contrário.
Portanto, podemos implementar várias portas lógicas e funções Booleanas apenas alterando os valores dos pesos e / ou valor do Limiar, T.
Exemplo
Deixe-nos encontrar o simplified Boolean function para a seguinte porta de limiar.

Esta porta de limiar tem três entradas X 1 , X 2 , X 3 e uma saída Y.
Os pesos correspondentes às entradas X 1 , X 2 e X 3 são W 1 = 2, W 2 = 1 e W 3 = -4 respectivamente.
O valor da porta de limiar é T = -1.
o weighted sum da porta de limiar é
$$W=W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}$$
Substitua os pesos dados na equação acima.
$$\Rightarrow W=2X_{1}+X_{2}-4X_{3}$$
A saída da porta de limiar, Y será '1' se W ≥ −1, caso contrário, será '0'.
Os seguintes table mostra a relação entre a entrada e a saída para todas as combinações possíveis de entradas.
| Entradas | Soma ponderada | Resultado | ||
|---|---|---|---|---|
| $X_{1}$ | $X_{2}$ | $X_{3}$ | $W=2X_{1}+X_{2}-4X_{3}$ | $Y$ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
A partir da tabela acima, podemos escrever o Boolean function para saída, Y como
$$Y= \sum m\left ( 0,2,4,6,7 \right )$$
A simplificação desta função booleana usando 3 variable K-Map é mostrado na figura a seguir.

Portanto, o simplified Boolean function pois determinado limiar é $Y={X_{3}'}+X_{1}X_{2}$.
Síntese de funções de limite
A porta de limiar também é chamada de universal gateporque podemos implementar qualquer função booleana usando portas de limiar. Às vezes, pode não ser possível implementar algumas portas lógicas e funções booleanas usando uma única porta de limiar. Nesse caso, podemos exigir várias portas Threshold.
Siga estes steps para implementar uma função booleana usando uma única porta de limiar.
Step 1 - Formule um Truth table para determinada função booleana.
Step 2 - Na tabela Verdade acima, adicione (inclua) mais uma coluna, que fornece a relação entre weighted sums e Threshold value.
Step 3 - Escreva a relação entre as somas ponderadas e o limite para cada combinação de entradas conforme mencionado abaixo.
Se a saída da função booleana for 1, a soma ponderada será maior ou igual ao valor do Limite para essa combinação de entradas.
Se a saída da função booleana for 0, a soma ponderada será menor que o valor do Limite para essa combinação de entradas.
Step 4 - Escolher os valores dos pesos e Limiares de forma que satisfaçam todas as relações presentes na última coluna da tabela acima.
step 5 - Desenhe o symbol da porta de limiar com esses pesos e valor de limiar.
Exemplo
Vamos implementar o seguinte Boolean function usando uma única porta de limiar.
$$Y\left ( X_{1},X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$$
A função booleana fornecida é uma função de três variáveis, que é representada na forma da soma dos termos mínimos. oTruth table desta função é mostrado abaixo.
| Entradas | Resultado | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Agora, vamos adicionar (incluir) mais uma coluna à tabela da Verdade acima. Esta última coluna contém as relações entreweighted sums (W) and Threshold valor (T) para cada combinação de entradas.
| Entradas | Resultado | Relações entre W & T | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <T |
| 1 | 0 | 0 | 1 | W 1 ≥ T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <T |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ T |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ T |
A seguir estão as conclusões da tabela acima.
O valor do Limiar deve ser zero ou negativo com base na primeira relação.
O valor de W 3 deve ser negativo com base na primeira e na segunda relações.
Os valores de W 1 e W 2 devem ser maiores ou iguais ao valor limite com base na quinta e terceira relações.
W 2 deve ser maior que W 3 com base na quarta relação.
Podemos escolher os seguintes valores para pesos e Limiar com base nas conclusões acima.
W 1 = 2, W 2 = 1, W 3 = -4 & T = -1
o symbol de Threshold gate com os valores acima é mostrado abaixo.

Portanto, esta porta de limiar implementa o dado Boolean function, $Y\left ( X_{1}, X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$.
Discutimos vários circuitos combinacionais nos capítulos anteriores. Todos esses circuitos possuem um conjunto de saída (s), que depende apenas da combinação das entradas presentes. A figura a seguir mostra oblock diagram do circuito sequencial.
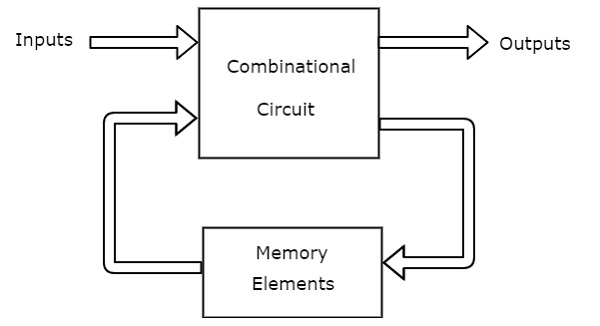
Este circuito sequencial contém um conjunto de entradas e saídas. A (s) saída (s) do circuito sequencial depende não apenas da combinação das entradas presentes, mas também da (s) saída (s) anterior (es). O resultado anterior nada mais é do que opresent state. Portanto, os circuitos sequenciais contêm circuitos combinacionais junto com elementos de memória (armazenamento). Alguns circuitos sequenciais podem não conter circuitos combinacionais, mas apenas elementos de memória.
A tabela a seguir mostra o differences entre circuitos combinacionais e circuitos sequenciais.
| Circuitos Combinacionais | Circuitos Sequenciais |
|---|---|
| As saídas dependem apenas das entradas atuais. | As saídas dependem das entradas e do estado atual. |
| O caminho de feedback não está presente. | O caminho de feedback está presente. |
| Elementos de memória não são necessários. | Elementos de memória são obrigatórios. |
| O sinal do relógio não é necessário. | O sinal do relógio é necessário. |
| Fácil de projetar. | Difícil de projetar. |
Tipos de circuitos sequenciais
A seguir estão os dois tipos de circuitos sequenciais -
- Circuitos sequenciais assíncronos
- Circuitos sequenciais síncronos
Circuitos sequenciais assíncronos
Se algumas ou todas as saídas de um circuito sequencial não mudam (afetam) em relação à transição ativa do sinal de relógio, então esse circuito sequencial é chamado de Asynchronous sequential circuit. Isso significa que todas as saídas de circuitos sequenciais assíncronos não mudam (afetam) ao mesmo tempo. Portanto, a maioria das saídas de circuitos sequenciais assíncronos sãonot in synchronous com apenas bordas positivas ou apenas bordas negativas do sinal de clock.
Circuitos sequenciais síncronos
Se todas as saídas de um circuito sequencial mudam (afetam) em relação à transição ativa do sinal de relógio, então esse circuito sequencial é chamado de Synchronous sequential circuit. Isso significa que todas as saídas dos circuitos sequenciais síncronos mudam (afetam) ao mesmo tempo. Portanto, as saídas dos circuitos sequenciais síncronos estão em sincronia apenas com as bordas positivas ou apenas com as bordas negativas do sinal de clock.
Sinal de relógio e disparo
Nesta seção, vamos discutir sobre o sinal de clock e os tipos de acionamento um por um.
Sinal do relógio
O sinal do relógio é um sinal periódico e sua hora de ativação e desativação não precisa ser a mesma. Podemos representar o sinal do relógio como umsquare wave, quando o tempo de LIGADO e o tempo de DESLIGADO são iguais. Este sinal de clock é mostrado na figura a seguir.

Na figura acima, a onda quadrada é considerada um sinal de clock. Este sinal permanece em nível lógico alto (5 V) por algum tempo e permanece em nível lógico baixo (0 V) por igual período de tempo. Este padrão se repete com algum período de tempo. Neste caso, otime period será igual a duas vezes do tempo LIGADO ou duas vezes do tempo DESLIGADO.
Podemos representar o sinal do relógio como train of pulses, quando a hora ON e a hora OFF não são iguais. Este sinal de clock é mostrado na figura a seguir.

Na figura acima, o trem de pulsos é considerado um sinal de relógio. Este sinal permanece na lógica Alta (5 V) por algum tempo e permanece na lógica Baixa (0 V) por algum outro tempo. Este padrão se repete com algum período de tempo. Neste caso, otime period será igual à soma do tempo ON e o tempo OFF.
O recíproco do período de tempo do sinal do relógio é conhecido como o frequencydo sinal do relógio. Todos os circuitos sequenciais são operados com sinal de relógio. Portanto, a frequência na qual os circuitos sequenciais podem ser operados de acordo com a frequência do sinal do relógio deve ser escolhida.
Tipos de acionamento
A seguir estão os dois tipos possíveis de disparo que são usados em circuitos sequenciais.
- Nível de ativação
- Edge triggering
Nível de ativação
Existem dois níveis, ou seja, lógico alto e lógico baixo no sinal de clock. A seguir estão os doistypes of level triggering.
- Disparo de nível positivo
- Acionamento de nível negativo
Se o circuito sequencial for operado com o sinal do relógio quando estiver em Logic High, então esse tipo de acionamento é conhecido como Positive level triggering. É destacado na figura abaixo.
Se o circuito sequencial for operado com o sinal do relógio quando estiver em Logic Low, então esse tipo de acionamento é conhecido como Negative level triggering. Ele é destacado na figura a seguir.

Edge triggering
Existem dois tipos de transições que ocorrem no sinal de clock. Isso significa que o sinal do clock muda de Logic Low para Logic High ou Logic High para Logic Low.
A seguir estão os dois types of edge triggering com base nas transições do sinal do relógio.
- Acionamento de borda positiva
- Acionamento de borda negativa
Se o circuito sequencial é operado com o sinal de clock que está em transição de Logic Low para Logic High, então esse tipo de acionamento é conhecido como Positive edge triggering. Também é chamado de disparo de borda ascendente. Isso é mostrado na figura a seguir.

Se o circuito sequencial é operado com o sinal de clock que está em transição de Logic High para Logic Low, então esse tipo de acionamento é conhecido como Negative edge triggering. Também é chamado de disparo de borda descendente. Isso é mostrado na figura a seguir.

Nos próximos capítulos, discutiremos sobre vários circuitos sequenciais com base no tipo de disparo que pode ser usado nele.
Existem dois tipos de elementos de memória com base no tipo de acionamento adequado para operá-lo.
- Latches
- Flip-flops
As travas operam com sinal de habilitação, que é level sensitive. Enquanto os flip-flops são sensíveis às bordas. Discutiremos sobre flip-flops no próximo capítulo. Agora, vamos discutir sobre SR Latch & D Latch um por um.
Trava SR
SR Latch também é chamado de Set Reset Latch. Esta trava afeta as saídas enquanto a habilitação E é mantida em '1'. ocircuit diagram de SR Latch é mostrado na figura a seguir.
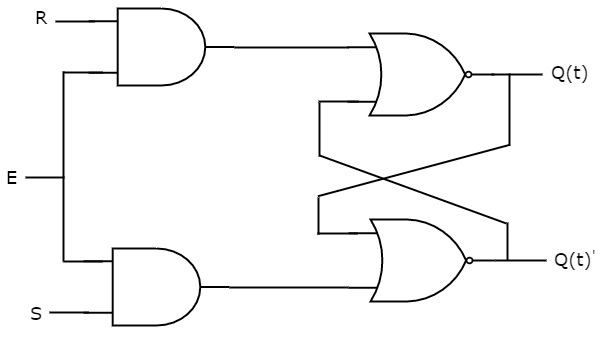
Este circuito tem duas entradas S e R e duas saídas Q (t) e Q (t) '. oupper NOR gate tem duas entradas R & complemento do estado presente, Q (t) 'e produz o próximo estado, Q (t + 1) quando habilitado, E é' 1 '.
Da mesma forma, o lower NOR gate tem duas entradas S & estado presente, Q (t) e produz complemento do próximo estado, Q (t + 1) 'quando habilitado, E é' 1 '.
Nós sabemos que um 2-input NOR gateproduz uma saída, que é o complemento de outra entrada quando uma das entradas é '0'. Da mesma forma, ele produz saída '0', quando uma das entradas é '1'.
Se S = 1, então o próximo estado Q (t + 1) será igual a '1' independentemente do estado presente, valores de Q (t).
Se R = 1, então o próximo estado Q (t + 1) será igual a '0' independentemente do estado presente, valores de Q (t).
A qualquer momento, apenas uma dessas duas entradas deve ser '1'. Se ambas as entradas forem '1', então o próximo valor de estado Q (t + 1) é indefinido.
A tabela a seguir mostra o state table de trava SR.
| S | R | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Portanto, SR Latch executa três tipos de funções, como Hold, Set & Reset com base nas condições de entrada.
Trava D
Existe uma desvantagem do SR Latch. Esse é o próximo valor de estado que não pode ser previsto quando ambas as entradas S e R são uma. Portanto, podemos superar essa dificuldade com o D Latch. Também é chamado de Data Latch. ocircuit diagram de D Latch é mostrado na figura a seguir.

Este circuito possui uma única entrada D e duas saídas Q (t) e Q (t) '. D Latch é obtido a partir de SR Latch colocando um inversor entre as entradas S&R e conectando a entrada D a S. Isso significa que eliminamos as combinações de S&R com o mesmo valor.
Se D = 0 → S = 0 & R = 1, então o próximo estado Q (t + 1) será igual a '0' independentemente do estado presente, valores de Q (t). Isso corresponde à segunda linha da tabela de estado SR Latch.
Se D = 1 → S = 1 & R = 0, então o próximo estado Q (t + 1) será igual a '1' independentemente do estado presente, valores de Q (t). Isso corresponde à terceira linha da tabela de estado SR Latch.
A tabela a seguir mostra o state table de D trava.
| D | Q (t + 1) |
|---|---|
| 0 | 0 |
| 1 | 1 |
Portanto, D Latch Retém as informações que estão disponíveis na entrada de dados, D. Isso significa que a saída de D Latch é sensível às mudanças na entrada, D, desde que a habilitação seja Alta.
Neste capítulo, implementamos várias travas fornecendo o acoplamento cruzado entre as portas NOR. Da mesma forma, você pode implementar essas travas usando portas NAND.
No capítulo anterior, discutimos sobre travas. Esses são os blocos básicos de construção de flip-flops. Podemos implementar flip-flops em dois métodos.
No primeiro método, cascade two latchesde tal forma que a primeira trava é habilitada para cada pulso de relógio positivo e a segunda trava é habilitada para cada pulso de relógio negativo. Para que a combinação dessas duas travas se torne um flip-flop.
No segundo método, podemos implementar diretamente o flip-flop, que é sensível à borda. Neste capítulo, vamos discutir o seguinteflip-flops usando o segundo método.
- SR Flip-Flop
- D Flip-Flop
- JK Flip-Flop
- Flip-flop T
SR Flip-Flop
O flip-flop SR opera apenas com transições de clock positivas ou negativas. Enquanto a trava SR opera com sinal de habilitação. ocircuit diagram de flip-flop SR é mostrado na figura a seguir.

Este circuito tem duas entradas S e R e duas saídas Q (t) e Q (t) '. A operação do flipflop SR é semelhante ao SR Latch. Porém, este flip-flop afeta as saídas apenas quando a transição positiva do sinal de clock é aplicada em vez de habilitação ativa.
A tabela a seguir mostra o state table de flip-flop SR.
| S | R | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Aqui, Q (t) e Q (t + 1) são o estado presente e o próximo estado, respectivamente. Portanto, SR flip-flop pode ser usado para uma dessas três funções, como Hold, Reset e Set com base nas condições de entrada, quando a transição positiva do sinal de clock é aplicada. A tabela a seguir mostra ocharacteristic table de flip-flop SR.
| Entradas presentes | Estado atual | Próximo estado | |
|---|---|---|---|
| S | R | Q(t) | Q(t + 1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | x |
| 1 | 1 | 1 | x |
Usando três variáveis K-Map, podemos obter a expressão simplificada para o próximo estado, Q (t + 1). othree variable K-Map para o próximo estado, Q (t + 1) é mostrado na figura a seguir.

Os agrupamentos máximos possíveis de adjacentes já são mostrados na figura. Portanto, osimplified expression para o próximo estado Q (t + 1) é
$Q\left ( t+1 \right )=S+{R}'Q\left ( t \right )$
D Flip-Flop
O flip-flop D opera apenas com transições de clock positivas ou negativas. Enquanto a trava D opera com sinal de habilitação. Isso significa que a saída do flip-flop D é insensível às mudanças na entrada, D exceto para a transição ativa do sinal de clock. ocircuit diagram de D flip-flop é mostrado na figura a seguir.

Este circuito possui uma única entrada D e duas saídas Q (t) e Q (t) '. A operação do flip-flop D é semelhante ao D Latch. Porém, este flip-flop afeta as saídas apenas quando a transição positiva do sinal de clock é aplicada em vez de habilitação ativa.
A tabela a seguir mostra o state table de D flip-flop.
| D | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Portanto, o flip-flop D sempre mantém a informação, que está disponível na entrada de dados, D da transição positiva anterior do sinal de clock. A partir da tabela de estados acima, podemos escrever diretamente a próxima equação de estado como
Q (t + 1) = D
O próximo estado do flip-flop D é sempre igual à entrada de dados, D para cada transição positiva do sinal de clock. Portanto, flip-flops D podem ser usados em registradores,shift registers e alguns dos contadores.
JK Flip-Flop
O flip-flop JK é a versão modificada do flip-flop SR. Ele opera apenas com transições de clock positivas ou negativas. ocircuit diagram do flip-flop JK é mostrado na figura a seguir.
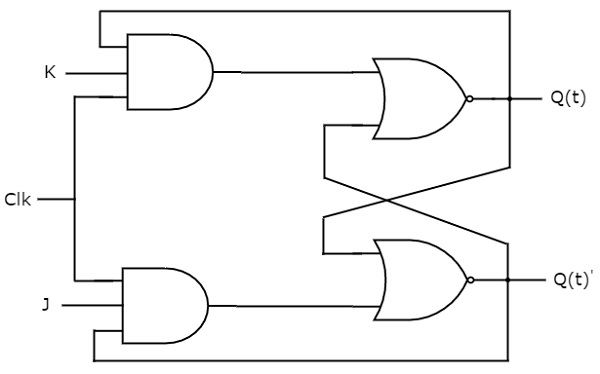
Este circuito possui duas entradas J e K e duas saídas Q (t) e Q (t) '. A operação do flip-flop JK é semelhante ao flip-flop SR. Aqui, consideramos as entradas do flip-flop SR comoS = J Q(t)’ e R = KQ(t) para utilizar o flip-flop SR modificado para 4 combinações de entradas.
A tabela a seguir mostra o state table de flip-flop JK.
| J | K | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q (t) ' |
Aqui, Q (t) e Q (t + 1) são o estado presente e o próximo estado, respectivamente. Portanto, o flip-flop JK pode ser usado para uma dessas quatro funções, como Hold, Reset, Set & Complement of current state com base nas condições de entrada, quando a transição positiva do sinal de clock é aplicada. A tabela a seguir mostra ocharacteristic table de flip-flop JK.
| Entradas presentes | Estado atual | Próximo estado | |
|---|---|---|---|
| J | K | Q(t) | Q(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Usando três variáveis K-Map, podemos obter a expressão simplificada para o próximo estado, Q (t + 1). Three variable K-Map para o próximo estado, Q (t + 1) é mostrado na figura a seguir.

Os agrupamentos máximos possíveis de adjacentes já são mostrados na figura. Portanto, osimplified expression para o próximo estado Q (t + 1) é
$$Q\left ( t+1 \right )=J{Q\left ( t \right )}'+{K}'Q\left ( t \right )$$
Flip-flop T
O flip-flop T é a versão simplificada do flip-flop JK. É obtido conectando a mesma entrada 'T' a ambas as entradas do flip-flop JK. Ele opera apenas com transições de clock positivas ou negativas. ocircuit diagram de flip-flop T é mostrado na figura a seguir.

Este circuito possui uma única entrada T e duas saídas Q (t) e Q (t) '. A operação do flip-flop T é a mesma do flip-flop JK. Aqui, consideramos as entradas do flip-flop JK comoJ = T e K = Ta fim de utilizar o flip-flop JK modificado para 2 combinações de entradas. Assim, eliminamos as outras duas combinações de J e K, para as quais esses dois valores são complementares entre si no flip-flop T.
A tabela a seguir mostra o state table de T flip-flop.
| D | Q (t + 1) |
|---|---|
| 0 | Q (t) |
| 1 | Q (t) ' |
Aqui, Q (t) e Q (t + 1) são o estado presente e o próximo estado, respectivamente. Assim, o flip-flop T pode ser usado para uma dessas duas funções, como Hold e Complement of current state com base nas condições de entrada, quando a transição positiva do sinal de clock é aplicada. A tabela a seguir mostra ocharacteristic table de T flip-flop.
| Entradas | Estado atual | Próximo estado |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
A partir da tabela de características acima, podemos escrever diretamente o next state equation Como
$$Q\left ( t+1 \right )={T}'Q\left ( t \right )+TQ{\left ( t \right )}'$$
$$\Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$
A saída do flip-flop T sempre alterna para cada transição positiva do sinal de clock, quando a entrada T permanece na lógica High (1). Assim, flip-flop T pode ser usado emcounters.
Neste capítulo, implementamos vários flip-flops fornecendo o acoplamento cruzado entre as portas NOR. Da mesma forma, você pode implementar esses flip-flops usando portas NAND.
No capítulo anterior, discutimos os quatro flip-flops, ou seja, flip-flop SR, flip-flop D, flip-flop JK e flip-flop T. Podemos converter um flip-flop nos três flip-flops restantes incluindo alguma lógica adicional. Portanto, haverá um total de dozeflip-flop conversions.
Siga estes steps para converter um flip-flop para o outro.
Considere o characteristic table do flip-flop desejado.
Preencha os valores de excitação (entradas) de determinado flip-flop para cada combinação de estado presente e próximo estado. oexcitation table para todos os flip-flops é mostrado abaixo.
| Estado atual | Próximo estado | Entradas SR flip-flop | Entrada flip-flop D | Entradas de flip-flop JK | Entrada de flip-flop T | ||
|---|---|---|---|---|---|---|---|
| Q(t) | Q(t+1) | S | R | D | J | K | T |
| 0 | 0 | 0 | x | 0 | 0 | x | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | x | 1 |
| 1 | 0 | 0 | 1 | 0 | x | 1 | 1 |
| 1 | 1 | x | 0 | 1 | x | 0 | 0 |
Pegue o simplified expressionspara cada entrada de excitação. Se necessário, use Kmaps para simplificar.
Desenhe o circuit diagram do flip-flop desejado de acordo com as expressões simplificadas usando o flip-flop dado e as portas lógicas necessárias.
Agora, vamos converter alguns flip-flops em outros. Siga o mesmo processo para as conversões de flipflop restantes.
SR Flip-Flop para outras conversões de flip-flop
A seguir estão as três conversões possíveis de flip-flop SR para outros flip-flops.
- Flip-flop SR para flip-flop D
- Flip-flop SR para flip-flop JK
- SR flip-flop para T flip-flop
Conversão de flip-flop SR para flip-flop D
Aqui, o flip-flop fornecido é o flip-flop SR e o flip-flop desejado é o flip-flop D. Portanto, considere o seguintecharacteristic table de D flip-flop.
| Entrada flip-flop D | Estado atual | Próximo estado |
|---|---|---|
| D | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Sabemos que o flip-flop SR tem duas entradas S e R. Portanto, anote os valores de excitação do flip-flop SR para cada combinação dos valores do estado presente e do próximo estado. A tabela a seguir mostra a tabela de características do flip-flop D junto com oexcitation inputs de flip-flop SR.
| Entrada flip-flop D | Estado atual | Próximo estado | Entradas SR flip-flop | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | S | R |
| 0 | 0 | 0 | 0 | x |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | x | 0 |
A partir da tabela acima, podemos escrever o Boolean functions para cada entrada conforme abaixo.
$$S=m_{2}+d_{3}$$
$$R=m_{1}+d_{0}$$
Podemos usar 2 K-Maps variáveis para obter expressões simplificadas para essas entradas. ok-Maps para S & R são mostrados abaixo.

Então, temos S = D & R = D 'após simplificar. ocircuit diagram de D flip-flop é mostrado na figura a seguir.

Este circuito consiste em um flip-flop SR e um inversor. Este inversor produz uma saída, que é um complemento da entrada, D. Portanto, o circuito geral tem uma única entrada, D e duas saídas Q (t) e Q (t) '. Portanto, é umD flip-flop. Da mesma forma, você pode fazer outras duas conversões.
D Flip-flop para outras conversões de flip-flop
A seguir estão as três conversões possíveis de flip-flop D para outros flip-flops.
- D flip-flop para T flip-flop
- D flip-flop para SR flip-flop
- D flip-flop para JK flip-flop
Conversão de flip-flop D para flip-flop T
Aqui, o flip-flop fornecido é flip-flop D e o flip-flop desejado é flip-flop T. Portanto, considere o seguintecharacteristic table de T flip-flop.
| Entrada de flip-flop T | Estado atual | Próximo estado |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Sabemos que o flip-flop D tem uma única entrada D. Portanto, anote os valores de excitação do flip-flop D para cada combinação dos valores do estado presente e do próximo estado. A tabela a seguir mostra a tabela de características do flip-flop T junto com oexcitation input de D flip-flop.
| Entrada de flip-flop T | Estado atual | Próximo estado | Entrada flip-flop D |
|---|---|---|---|
| T | Q(t) | Q(t + 1) | D |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
A partir da tabela acima, podemos escrever diretamente o Boolean function de D como abaixo.
$$D=T\oplus Q\left ( t \right )$$
Portanto, exigimos uma porta OU Exclusivo de duas entradas junto com o flip-flop D. ocircuit diagram de flip-flop T é mostrado na figura a seguir.

Este circuito consiste em um flip-flop D e uma porta OU exclusiva. Essa porta OU exclusiva produz uma saída, que é Ex-OR de T e Q (t). Portanto, o circuito geral tem uma única entrada, T e duas saídas Q (t) e Q (t) '. Portanto, é umT flip-flop. Da mesma forma, você pode fazer outras duas conversões.
JK flip-flop para outras conversões de flip-flop
A seguir estão as três conversões possíveis de flip-flop JK para outros flip-flops.
- Flip-flop JK para flip-flop T
- Flip-flop JK para flip-flop D
- Flip-flop JK para flip-flop SR
Conversão de flip-flop JK para flip-flop T
Aqui, o flip-flop fornecido é o flip-flop JK e o flip-flop desejado é o flip-flop T. Portanto, considere o seguintecharacteristic table de T flip-flop.
| Entrada de flip-flop T | Estado atual | Próximo estado |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Sabemos que o flip-flop JK tem duas entradas J e K. Portanto, anote os valores de excitação do flip-flop JK para cada combinação dos valores do estado presente e do próximo estado. A tabela a seguir mostra a tabela de características do flip-flop T junto com oexcitation inputs de flipflop JK.
| Entrada de flip-flop T | Estado atual | Próximo estado | Entradas de flip-flop JK | |
|---|---|---|---|---|
| T | Q(t) | Q(t + 1) | J | K |
| 0 | 0 | 0 | 0 | x |
| 0 | 1 | 1 | x | 0 |
| 1 | 0 | 1 | 1 | x |
| 1 | 1 | 0 | x | 1 |
A partir da tabela acima, podemos escrever o Boolean functions para cada entrada conforme abaixo.
$$J=m_{2}+d_{1}+d_{3}$$
$$K=m_{3}+d_{0}+d_{2}$$
Podemos usar 2 K-Maps variáveis para obter expressões simplificadas para essas duas entradas. ok-Maps para J & K são mostrados abaixo.

Então, temos, J = T & K = T após simplificar. ocircuit diagram de flip-flop T é mostrado na figura a seguir.

Este circuito consiste apenas em flip-flop JK. Não requer nenhum outro portão. Basta conectar a mesma entrada T a ambos J e K. Assim, o circuito geral tem uma única entrada, T e duas saídas Q (t) e Q (t) '. Portanto, é umT flip-flop. Da mesma forma, você pode fazer outras duas conversões.
T flip-flop para outras conversões de flip-flop
A seguir estão as três conversões possíveis de flip-flop T para outros flip-flops.
- Flip-flop T para flip-flop D
- Flip-flop T para flip-flop SR
- Flip-flop T para flip-flop JK
Conversão de flip-flop T em flip-flop D
Aqui, o flip-flop fornecido é o flip-flop T e o flip-flop desejado é o flip-flop D. Portanto, considere a tabela de características do flip-flop D e anote os valores de excitação do flip-flop T para cada combinação dos valores do estado presente e do próximo estado. A tabela a seguir mostra ocharacteristic table de D flip-flop junto com o excitation input of T flip-flop.
| D flip-flop input | Present State | Next State | T flip-flop input | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | T | |
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | |
From the above table, we can directly write the Boolean function of T as below.
$$T=D\oplus Q\left ( t \right )$$
So, we require a two input Exclusive-OR gate along with T flip-flop. The circuit diagram of D flip-flop is shown in the following figure.

This circuit consists of T flip-flop and an Exclusive-OR gate. This Exclusive-OR gate produces an output, which is Ex-OR of D and Q(t). So, the overall circuit has single input, D and two outputs Q(t) & Q(t)’. Hence, it is a D flip-flop. Similarly, you can do other two conversions.
We know that one flip-flop can store one-bit of information. In order to store multiple bits of information, we require multiple flip-flops. The group of flip-flops, which are used to hold (store) the binary data is known as register.
If the register is capable of shifting bits either towards right hand side or towards left hand side is known as shift register. An ‘N’ bit shift register contains ‘N’ flip-flops. Following are the four types of shift registers based on applying inputs and accessing of outputs.
- Serial In − Serial Out shift register
- Serial In − Parallel Out shift register
- Parallel In − Serial Out shift register
- Parallel In − Parallel Out shift register
Serial In − Serial Out (SISO) Shift Register
The shift register, which allows serial input and produces serial output is known as Serial In – Serial Out (SISO) shift register. The block diagram of 3-bit SISO shift register is shown in the following figure.

This block diagram consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can send the bits serially from the input of left most D flip-flop. Hence, this input is also called as serial input. For every positive edge triggering of clock signal, the data shifts from one stage to the next. So, we can receive the bits serially from the output of right most D flip-flop. Hence, this output is also called as serial output.
Example
Let us see the working of 3-bit SISO shift register by sending the binary information “011” from LSB to MSB serially at the input.
Assume, initial status of the D flip-flops from leftmost to rightmost is $Q_{2}Q_{1}Q_{0}=000$. We can understand the working of 3-bit SISO shift register from the following table.
| No of positive edge of Clock | Serial Input | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1(LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0(MSB) | 0 | 1 | 1(LSB) |
| 4 | - | - | 0 | 1 |
| 5 | - | - | - | 0(MSB) |
The initial status of the D flip-flops in the absence of clock signal is $Q_{2}Q_{1}Q_{0}=000$. Here, the serial output is coming from $Q_{0}$. So, the LSB (1) is received at 3rd positive edge of clock and the MSB (0) is received at 5th positive edge of clock.
Therefore, the 3-bit SISO shift register requires five clock pulses in order to produce the valid output. Similarly, the N-bit SISO shift register requires 2N-1 clock pulses in order to shift ‘N’ bit information.
Serial In - Parallel Out (SIPO) Shift Register
The shift register, which allows serial input and produces parallel output is known as Serial In – Parallel Out (SIPO) shift register. The block diagram of 3-bit SIPO shift register is shown in the following figure.
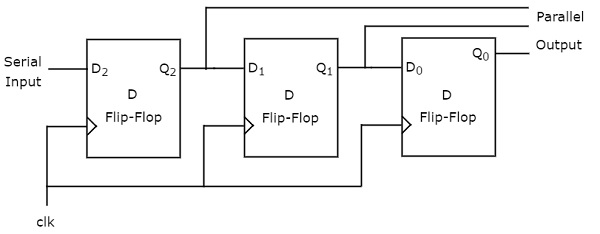
This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can send the bits serially from the input of left most D flip-flop. Hence, this input is also called as serial input. For every positive edge triggering of clock signal, the data shifts from one stage to the next. In this case, we can access the outputs of each D flip-flop in parallel. So, we will get parallel outputs from this shift register.
Example
Let us see the working of 3-bit SIPO shift register by sending the binary information “011” from LSB to MSB serially at the input.
Assume, initial status of the D flip-flops from leftmost to rightmost is $Q_{2}Q_{1}Q_{0}=000$. Here, $Q_{2}$ & $Q_{0}$ are MSB & LSB respectively. We can understand the working of 3-bit SIPO shift register from the following table.
| No of positive edge of Clock | Serial Input | Q2(MSB) | Q1 | Q0(LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1(LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0(MSB) | 0 | 1 | 1 |
The initial status of the D flip-flops in the absence of clock signal is $Q_{2}Q_{1}Q_{0}=000$. The binary information “011” is obtained in parallel at the outputs of D flip-flops for third positive edge of clock.
So, the 3-bit SIPO shift register requires three clock pulses in order to produce the valid output. Similarly, the N-bit SIPO shift register requires N clock pulses in order to shift ‘N’ bit information.
Parallel In − Serial Out (PISO) Shift Register
The shift register, which allows parallel input and produces serial output is known as Parallel In − Serial Out (PISO) shift register. The block diagram of 3-bit PISO shift register is shown in the following figure.

This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can apply the parallel inputs to each D flip-flop by making Preset Enable to 1. For every positive edge triggering of clock signal, the data shifts from one stage to the next. So, we will get the serial output from the right most D flip-flop.
Example
Let us see the working of 3-bit PISO shift register by applying the binary information “011” in parallel through preset inputs.
Since the preset inputs are applied before positive edge of Clock, the initial status of the D flip-flops from leftmost to rightmost will be $Q_{2}Q_{1}Q_{0}=011$. We can understand the working of 3-bit PISO shift register from the following table.
| No of positive edge of Clock | Q2 | Q1 | Q0 |
|---|---|---|---|
| 0 | 0 | 1 | 1(LSB) |
| 1 | - | 0 | 1 |
| 2 | - | - | 0(LSB) |
Here, the serial output is coming from $Q_{0}$. So, the LSB (1) is received before applying positive edge of clock and the MSB (0) is received at 2nd positive edge of clock.
Therefore, the 3-bit PISO shift register requires two clock pulses in order to produce the valid output. Similarly, the N-bit PISO shift register requires N-1 clock pulses in order to shift ‘N’ bit information.
Parallel In - Parallel Out (PIPO) Shift Register
The shift register, which allows parallel input and produces parallel output is known as Parallel In − Parallel Out (PIPO) shift register. The block diagram of 3-bit PIPO shift register is shown in the following figure.

This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can apply the parallel inputs to each D flip-flop by making Preset Enable to 1. We can apply the parallel inputs through preset or clear. These two are asynchronous inputs. That means, the flip-flops produce the corresponding outputs, based on the values of asynchronous inputs. In this case, the effect of outputs is independent of clock transition. So, we will get the parallel outputs from each D flip-flop.
Exemplo
Vamos ver o funcionamento do registrador de deslocamento PIPO de 3 bits aplicando as informações binárias “011” em paralelo por meio de entradas predefinidas.
Uma vez que as entradas predefinidas são aplicadas antes da borda positiva do relógio, o status inicial dos flip-flops D da extrema esquerda para a direita $Q_{2}Q_{1}Q_{0}=011$. Então, a informação binária“011” é obtido em paralelo nas saídas dos flip-flops D antes de aplicar a borda positiva do clock.
Portanto, o registro de deslocamento PIPO de 3 bits requer pulsos de clock zero para produzir a saída válida. Da mesma forma, oN-bit PIPO shift register não requer nenhum pulso de clock para mudar a informação do bit 'N'.
No capítulo anterior, discutimos quatro tipos de registradores de deslocamento. Com base no requisito, podemos usar um desses registradores de deslocamento. A seguir estão as aplicações dos registradores de deslocamento.
O registro de deslocamento é usado como Parallel to serial converter, que converte os dados paralelos em dados seriais. É utilizado na seção do transmissor após o bloco do conversor analógico para digital (ADC).
O registro de deslocamento é usado como Serial to parallel converter, que converte os dados seriais em dados paralelos. É utilizado na seção do receptor antes do bloco do conversor digital para analógico (DAC).
O registrador de deslocamento junto com algumas portas adicionais geram a seqüência de zeros e uns. Portanto, é usado comosequence generator.
Registradores de deslocamento também são usados como counters. Existem dois tipos de contadores com base no tipo de saída do flip-flop D mais à direita conectado à entrada serial. Esses são contador Ring e contador Johnson Ring.
Neste capítulo, vamos discutir sobre esses dois contadores, um por um.
Contador de anéis
No capítulo anterior, discutimos a operação de Serial In - Parallel Out (SIPO)registro de deslocamento. Ele aceita os dados externos na forma serial e requer pulsos de clock 'N' para mudar os dados de bit 'N'.
Similarmente, ‘N’ bit Ring counterexecuta a operação semelhante. Mas, a única diferença é que a saída do flip-flop D mais à direita é fornecida como entrada do flip-flop D mais à esquerda, em vez de aplicar dados externos. Portanto, o contador de anel produz uma sequência de estados (padrão de zeros e uns) e se repete a cada‘N’ clock cycles.
o block diagram do contador de anel de 3 bits é mostrado na figura a seguir.
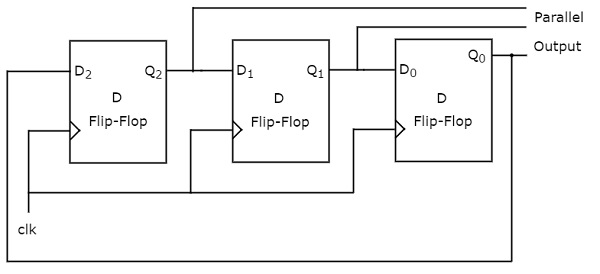
O contador de anel de 3 bits contém apenas um registro de deslocamento SIPO de 3 bits. A saída do flip-flop D mais à direita é conectada à entrada serial do flip-flop D mais à esquerda.
Suponha que o status inicial dos flip-flops D da extrema esquerda para a direita é $Q_{2}Q_{1}Q_{0}=001$. Aqui,$Q_{2}$ E $Q_{0}$são MSB e LSB, respectivamente. Podemos entender oworking of Ring counter da tabela a seguir.
| Nº de borda positiva do relógio | Entrada serial = Q 0 | Q 2 (MSB) | Q 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 |
O status inicial dos flip-flops D na ausência de sinal de clock é $Q_{2}Q_{1}Q_{0}=001$. Este status se repete para cada três transições de borda positiva do sinal de clock.
Portanto, o seguinte operations ocorrem para cada borda positiva do sinal de clock.
A entrada serial do primeiro flip-flop D obtém a saída anterior do terceiro flip-flop. Portanto, a saída atual do primeiro flip-flop D é igual à saída anterior do terceiro flip-flop.
As saídas anteriores do primeiro e do segundo flip-flops D são deslocadas um bit para a direita. Isso significa que as saídas presentes do segundo e terceiro flip-flops D são iguais às saídas anteriores do primeiro e segundo D flip-flops.
Johnson Ring Counter
A operação de Johnson Ring counteré semelhante ao contador de anel. Mas, a única diferença é que a saída complementada do flip-flop D mais à direita é fornecida como entrada do flip-flop D mais à esquerda em vez da saída normal. Portanto, o contador 'N' bit Johnson Ring produz uma sequência de estados (padrão de zeros e uns) e se repete a cada‘2N’ clock cycles.
O contador Johnson Ring também é chamado de Twisted Ring countere mudar o contador do anel da cauda. oblock diagram do contador Johnson Ring de 3 bits é mostrado na figura a seguir.

O contador Johnson Ring de 3 bits também contém apenas um registro de deslocamento SIPO de 3 bits. A saída complementada do flip-flop D mais à direita é conectada à entrada serial do flip-flop D mais à esquerda.
Suponha que inicialmente todos os flip-flops D sejam apagados. Então,$Q_{2}Q_{1}Q_{0}=000$. Aqui,$Q_{2}$ E $Q_{0}$são MSB e LSB, respectivamente. Podemos entender oworking do contador Johnson Ring da tabela a seguir.
| Nº de borda positiva do relógio | Entrada serial = Q 0 | Q 2 (MSB) | Q 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 1 | 1 |
| 5 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 |
O status inicial dos flip-flops D na ausência de sinal de clock é $Q_{2}Q_{1}Q_{0}=000$. Este status se repete para cada seis transições de borda positiva do sinal de clock.
Portanto, o seguinte operations ocorrem para cada borda positiva do sinal de clock.
A entrada serial do primeiro flip-flop D obtém a saída complementada anterior do terceiro flip-flop. Assim, a saída atual do primeiro flip-flop D é igual à saída complementada anterior do terceiro flip-flop.
As saídas anteriores do primeiro e do segundo flip-flops D são deslocadas um bit para a direita. Isso significa que as saídas presentes do segundo e terceiro flip-flops D são iguais às saídas anteriores do primeiro e segundo D flip-flops.
Nos dois capítulos anteriores, discutimos vários registros de deslocamento e counters using D flipflops. Agora, vamos discutir vários contadores usando flip-flops T. Sabemos que o flip-flop T alterna a saída para cada transição positiva do sinal de clock ou para cada transição negativa do sinal de clock.
Um contador binário 'N' bit consiste em flip-flops 'N' T. Se o contador contar de 0 a 2 - 1, então é chamado de binário up counter. Da mesma forma, se a contagem regressiva do contador a partir de 2 - 1 a 0, então é chamado de binário down counter.
São dois types of counters com base nos flip-flops que estão conectados em síncrono ou não.
- Contadores assíncronos
- Contadores síncronos
Contadores Assíncronos
Se os flip-flops não receberem o mesmo sinal de relógio, esse contador é chamado de Asynchronous counter. A saída do relógio do sistema é aplicada como sinal de relógio apenas ao primeiro flip-flop. Os flip-flops restantes recebem o sinal de clock da saída de seu flip-flop de estágio anterior. Conseqüentemente, as saídas de todos os flip-flops não mudam (afetam) ao mesmo tempo.
Agora, vamos discutir os dois contadores a seguir, um por um.
- Contador ascendente binário assíncrono
- Contador binário assíncrono descendente
Contador ascendente binário assíncrono
Um contador ascendente binário assíncrono de bit 'N' consiste em flip-flops 'N' T. Conta de 0 a 2 - 1. O block diagram de contador ascendente binário assíncrono de 3 bits é mostrado na figura a seguir.

O contador ascendente binário assíncrono de 3 bits contém três flip-flops T e a entrada T de todos os flip-flops é conectada a '1'. Todos esses flip-flops são acionados por borda negativa, mas as saídas mudam de forma assíncrona. O sinal do clock é aplicado diretamente ao primeiro T flip-flop. Então, a saída do primeiro T flip-floptoggles para cada borda negativa do sinal de clock.
A saída do primeiro flip-flop T é aplicada como sinal de clock para o segundo flip-flop T. Portanto, a saída do segundo flip-flop T alterna para cada borda negativa de saída do primeiro flip-flop T. Da mesma forma, a saída do terceiro flip-flop T alterna para cada borda negativa de saída do segundo flip-flop T, uma vez que a saída do segundo flip-flop T atua como o sinal de clock para o terceiro flip-flop T.
Assuma que o status inicial dos T flip-flops da extrema direita para a esquerda é $Q_{2}Q_{1}Q_{0}=000$. Aqui,$Q_{2}$ E $Q_{0}$são MSB e LSB, respectivamente. Podemos entender oworking de contador binário assíncrono de 3 bits da tabela a seguir.
| Nº de borda negativa do relógio | Q 0 (LSB) | Q 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 |
| 7 | 1 | 1 | 1 |
Aqui $Q_{0}$ alternado para cada borda negativa do sinal de clock. $Q_{1}$ alternado para todos $Q_{0}$que vai de 1 a 0, caso contrário, permaneceu no estado anterior. Similarmente,$Q_{2}$ alternado para todos $Q_{1}$ que vai de 1 a 0, caso contrário, permaneceu no estado anterior.
O status inicial dos flip-flops T na ausência de sinal de clock é $Q_{2}Q_{1}Q_{0}=000$. Isso é incrementado em um para cada borda negativa do sinal de clock e atingiu o valor máximo na 7ª borda negativa do sinal de clock. Este padrão se repete quando outras bordas negativas do sinal de clock são aplicadas.
Contador binário assíncrono inferior
Um contador descendente binário assíncrono de bit 'N' consiste em flip-flops 'N' T. Conta a partir de 2 - 1 a 0. O block diagram de contador descendente binário assíncrono de 3 bits é mostrado na figura a seguir.

O diagrama de blocos do contador ascendente binário assíncrono de 3 bits é semelhante ao diagrama de blocos do contador ascendente binário assíncrono de 3 bits. Mas, a única diferença é que em vez de conectar as saídas normais de um flip-flop de estágio como sinal de clock para o flip-flop de próximo estágio, conecte ocomplemented outputsde um flip-flop de estágio como sinal de clock para o flip-flop de próximo estágio. A saída complementada vai de 1 a 0 é igual à saída normal vai de 0 a 1.
Assuma que o status inicial dos T flip-flops da extrema direita para a esquerda é $Q_{2}Q_{1}Q_{0}=000$. Aqui,$Q_{2}$ E $Q_{0}$são MSB e LSB, respectivamente. Podemos entender oworking de contador inferior binário assíncrono de 3 bits da tabela a seguir.
| Nº de borda negativa do relógio | Q 0 (LSB) | Q 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 1 | 0 |
| 6 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 |
Aqui $Q_{0}$ alternado para cada borda negativa do sinal de clock. $Q_{1}$ alternado para todos $Q_{0}$que vai de 0 a 1, caso contrário, permaneceu no estado anterior. Similarmente,$Q_{2}$ alternado para todos $Q_{1}$ que vai de 0 a 1, caso contrário, permaneceu no estado anterior.
O status inicial dos flip-flops T na ausência de sinal de clock é $Q_{2}Q_{1}Q_{0}=000$. Este é decrementado em um para cada margem negativa de sinal de relógio e atinge o mesmo valor em 8 th flanco negativo de sinal de relógio. Este padrão se repete quando outras bordas negativas do sinal de clock são aplicadas.
Contadores síncronos
Se todos os flip-flops receberem o mesmo sinal de relógio, esse contador é chamado de Synchronous counter. Conseqüentemente, as saídas de todos os flip-flops mudam (afetam) ao mesmo tempo.
Agora, vamos discutir os dois contadores a seguir, um por um.
- Contador ascendente binário síncrono
- Contador binário síncrono para baixo
Contador ascendente binário síncrono
Um contador ascendente binário síncrono de 'N' bits consiste em flip-flops 'N' T. Conta de 0 a 2 - 1. O block diagram do contador ascendente binário síncrono de 3 bits é mostrado na figura a seguir.

O contador ascendente binário síncrono de 3 bits contém três flip-flops T e uma porta AND de 2 entradas. Todos esses flip-flops são acionados por borda negativa e as saídas dos flip-flops mudam (afetam) de forma síncrona. As entradas T do primeiro, segundo e terceiro flip-flops são 1,$Q_{0}$ E $Q_{1}Q_{0}$ respectivamente.
A saída do primeiro T flip-flop togglespara cada borda negativa do sinal de clock. A saída do segundo flip-flop T alterna para cada borda negativa do sinal de clock se$Q_{0}$ é 1. A saída do terceiro flip-flop T alterna para cada borda negativa do sinal de clock se ambos $Q_{0}$ E $Q_{1}$ são 1.
Contador binário síncrono inferior
Um contador descendente binário síncrono de 'N' bits consiste em flip-flops 'N' T. Conta a partir de 2 - 1 a 0. O block diagram de contador descendente binário síncrono de 3 bits é mostrado na figura a seguir.

O contador descendente binário síncrono de 3 bits contém três flip-flops T e uma porta AND de 2 entradas. Todos esses flip-flops são acionados por borda negativa e as saídas dos flip-flops mudam (afetam) de forma síncrona. As entradas T do primeiro, segundo e terceiro flip-flops são 1,${Q_{0}}'$ & ' ${Q_{1}}'$${Q_ {0}} '$ respectivamente.
A saída do primeiro T flip-flop togglespara cada borda negativa do sinal de clock. A saída do segundo flip-flop T alterna para cada borda negativa do sinal de clock se $ {Q_ {0}} '$ is 1. The output of third T flip-flop toggles for every negative edge of clock signal if both ${Q_ {1}} '$ & ${Q_ {0}} '$ são 1.
Sabemos que os circuitos sequenciais síncronos mudam (afetam) seus estados para cada transição positiva (ou negativa) do sinal de clock com base na entrada. Portanto, este comportamento de circuitos sequenciais síncronos pode ser representado na forma gráfica e é conhecido comostate diagram.
Um circuito sequencial síncrono também é chamado de Finite State Machine(FSM), se tiver número finito de estados. Existem dois tipos de FSMs.
- Mealy State Machine
- Moore State Machine
Agora, vamos discutir sobre essas duas máquinas de estado, uma por uma.
Mealy State Machine
Uma máquina de estados finitos é considerada uma máquina de estados de Mealy, se as saídas dependerem das entradas e dos estados presentes. oblock diagram da máquina de estado Mealy é mostrado na figura a seguir.
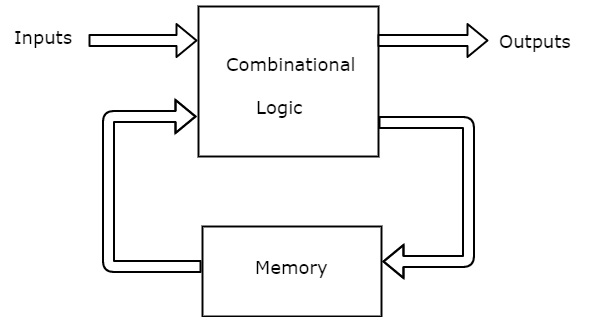
Conforme mostrado na figura, há duas partes presentes na máquina de estado de Mealy. Essas são lógica combinatória e memória. A memória é útil para fornecer algumas ou parte das saídas anteriores(present states) como entradas de lógica combinacional.
Portanto, com base nas entradas e nos estados presentes, a máquina de estados de Mealy produz saídas. Portanto, as saídas serão válidas apenas na transição positiva (ou negativa) do sinal de clock.
o state diagram da máquina de estado Mealy é mostrado na figura a seguir.
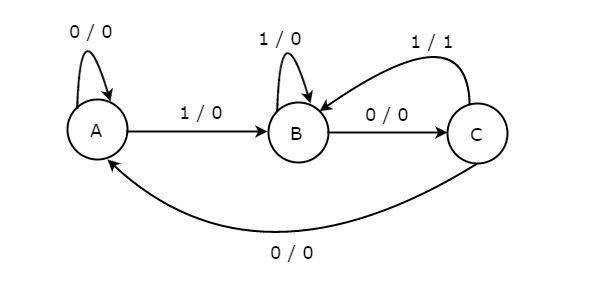
Na figura acima, existem três estados, a saber A, B e C. Esses estados são rotulados dentro dos círculos e cada círculo corresponde a um estado. As transições entre esses estados são representadas por linhas direcionadas. Aqui, 0/0, 1/0 e 1/1 denotainput / output. Na figura acima, existem duas transições de cada estado com base no valor da entrada, x.
Em geral, o número de estados exigidos na máquina de estados de Mealy é menor ou igual ao número de estados exigidos na máquina de estados de Moore. Há uma máquina de estado de Moore equivalente para cada máquina de estado de Mealy.
Moore State Machine
Uma máquina de estados finitos é considerada uma máquina de estados de Moore, se as saídas dependerem apenas dos estados presentes. oblock diagram da máquina de estado de Moore é mostrado na figura a seguir.

Conforme mostrado na figura, há duas partes presentes na máquina de estado de Moore. Essas são lógica combinatória e memória. Nesse caso, as entradas e os estados presentes determinam os próximos estados. Portanto, com base nos próximos estados, a máquina de estados de Moore produz as saídas. Portanto, as saídas serão válidas somente após a transição do estado.
o state diagram da máquina de estado de Moore é mostrado na figura a seguir.

Na figura acima, existem quatro estados, a saber, A, B, C e D. Esses estados e as respectivas saídas são rotulados dentro dos círculos. Aqui, apenas o valor de entrada é rotulado em cada transição. Na figura acima, existem duas transições de cada estado com base no valor da entrada, x.
Em geral, o número de estados necessários na máquina de estados de Moore é maior ou igual ao número de estados necessários na máquina de estados de Mealy. Há uma máquina de estado Mealy equivalente para cada máquina de estado de Moore. Portanto, com base no requisito, podemos usar um deles.
Cada digital systempode ser dividido em duas partes. Esses são circuitos de caminho de dados (digitais) e circuitos de controle. Os circuitos de caminho de dados executam funções como armazenamento de informações binárias (dados) e transferência de dados de um sistema para outro. Considerando que, os circuitos de controle determinam o fluxo de operações dos circuitos digitais.
É difícil descrever o comportamento de grandes máquinas de estado usando diagramas de estado. Para superar essa dificuldade, gráficos de máquina de estado algoritmo (ASM) podem ser usados.ASM chartssão semelhantes aos fluxogramas. Eles são usados para representar o fluxo de tarefas a serem executadas por circuitos de caminho de dados e circuitos de controle.
Componentes básicos de gráficos ASM
A seguir estão os três componentes básicos dos gráficos ASM.
- Caixa de estado
- Caixa de decisão
- Caixa de saída condicional
Caixa de estado
A caixa de estado é representada em forma retangular. Cada caixa de estado representa um estado do circuito sequencial. osymbol da caixa de estado é mostrada na figura a seguir.
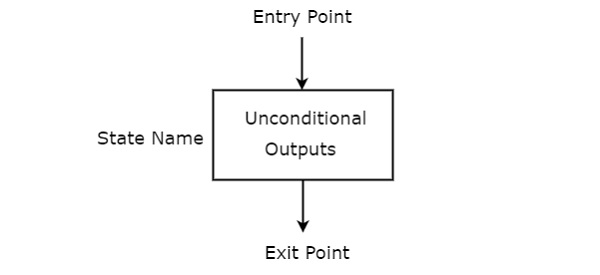
É ter um ponto de entrada e um ponto de saída. O nome do estado é colocado à esquerda da caixa do estado. As saídas incondicionais correspondentes a esse estado podem ser colocadas dentro da caixa de estado.Moore as saídas da máquina de estado também podem ser colocadas dentro da caixa de estado.
Caixa de decisão
A caixa de decisão é representada em forma de diamante. osymbol da caixa de decisão é mostrado na figura a seguir.

É ter um ponto de entrada e dois caminhos de saída. As entradas ou expressões booleanas podem ser colocadas dentro da caixa de decisão, que devem ser verificadas se são verdadeiras ou falsas. Se a condição for verdadeira, ele dará preferência ao path1. Caso contrário, ele preferirá o path2.
Caixa de saída condicional
A caixa de saída condicional é representada em forma oval. osymbol da caixa de saída condicional é mostrado na figura a seguir.

Ele também tem um ponto de entrada e um ponto de saída semelhante à caixa de estado. As saídas condicionais podem ser colocadas dentro da caixa de estado. Em geral,Mealyas saídas da máquina de estado são representadas dentro da caixa de saída condicional. Portanto, com base no requisito, podemos usar os componentes acima corretamente para desenhar gráficos ASM.