Encontrar a área de um trapézio em uma grade usando triângulos e retângulos

Introdução

Nesta lição, encontramos áreas de trapézios em grades usando triângulos e retângulos. Os trapézios são decompostos em triângulos e retângulos e suas áreas são encontradas. A soma dessas áreas fornece a área do trapézio na grade.

Conhecemos a área de um triângulo = $ \ frac {1} {2} $ b × he

área de um retângulo = l × w

Exemplo 1:

Encontre a área do trapézio a seguir usando triângulos e retângulos.

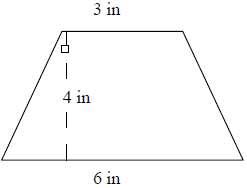
Solução

Step 1:

Área do triângulo direito = $ \ frac {1} {2} $ × b × h; b = base; h = altura.

Área de 2 triângulos retângulos = 2 × $ \ frac {1} {2} $ × b × h = 1,5 × 4 = 6 pol.

Step 2:

Área do retângulo = l × w = 4 × 3 = 12 quadrados em

Step 3:

Área do trapézio = Área dos triângulos + Área do retângulo

= 6 + 12

= 18 dentro

Exemplo 2:

Encontre a área do trapézio a seguir usando triângulos e retângulos.

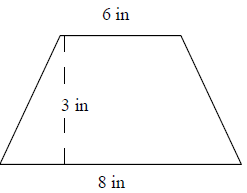
Solução

Step 1:

Área do triângulo direito = $ \ frac {1} {2} $ × b × h; b = base; h = altura.

Área de 2 triângulos retângulos = 2 × $ \ frac {1} {2} $ × b × h = 1 × 3 = 3 pol.

Step 2:

Área do retângulo = l × w = 6 × 3 = 18 quadrados em

Step 3:

Área do trapézio = Área dos triângulos + Área do retângulo

= 3 + 18

= 21 dentro do quadrado