Perímetro de uma figura retangular por partes
Nesta lição, encontramos o perímetro de determinadas figuras retangulares por partes.
Recebemos figuras retangulares por partes com algumas medidas, enquanto outras estão faltando. Primeiro encontramos esses comprimentos ausentes. Nessas figuras, presume-se que todos os lados que se cruzam se encontram em ângulos retos. É observado que os lados opostos de um retângulo são paralelos e iguais em comprimento ao calcular os comprimentos ausentes. Também dividimos a figura fornecida em dois retângulos para o mesmo propósito.
Uma vez que os comprimentos que faltam são encontrados, somando o comprimento ao longo do limite externo da figura dada dá o perímetro da figura dada.
Encontre o perímetro da figura a seguir. Observe que algum comprimento não é fornecido. Suponha que todos os lados que se cruzam se encontram em ângulos retos.
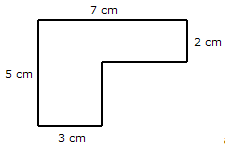
Solução
Step 1:
Comprimentos ausentes 7 - 3 = 4 cm; 5 - 2 = 3 cm
Step 2:
Perímetro da figura fornecida = 5 + 7 + 2 + 4 + 3 + 3 = 24 cm
Encontre o perímetro da figura a seguir. Observe que algum comprimento não é fornecido. Suponha que todos os lados que se cruzam se encontram em ângulos retos.
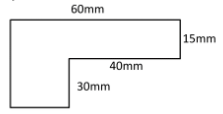
Solução
Step 1:
Comprimentos ausentes 60 - 40 = 20 mm; 30 + 15 = 45 mm
Step 2:
Perímetro da figura fornecida = 45 + 60 + 15 + 40 + 30 + 20 = 210 mm
Os lados opostos dos retângulos têm o mesmo comprimento.
Agora podemos encontrar o perímetro da figura adicionando todos os comprimentos.