Propriedades de Z-Transforms

Z-Transform tem as seguintes propriedades:

Propriedade de Linearidade

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

e $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Então a propriedade de linearidade afirma que

$ a \, x (n) + b \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} a \, X (Z) + b \, Y (Z) $

Propriedade Time Shifting

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Então a propriedade Time shifting afirma que

$ x (nm) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} z ^ {- m} X (Z) $

Propriedade de multiplicação por sequência exponencial

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Então, a multiplicação por uma propriedade de sequência exponencial afirma que

$ a ^ n \,. x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z / a) $

Propriedade de reversão do tempo

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Então, a propriedade de reversão do tempo afirma que

$ x (-n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (1 / Z) $

Diferenciação no domínio Z OU multiplicação pela propriedade n

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Então a multiplicação por n ou diferenciação na propriedade do domínio z afirma que

$ n ^ kx (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} [-1] ^ kz ^ k {d ^ k X (Z) \ sobre dZ ^ K} $

Propriedade de convolução

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

e $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Então a propriedade de convolução afirma que

$ x (n) * y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z) $

Propriedade de Correlação

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

e $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Então, a propriedade de correlação afirma que

$ x (n) \ otimes y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z ^ {- 1}) $

Teoremas do valor inicial e do valor final

Os teoremas do valor inicial e do valor final da transformada z são definidos para o sinal causal.

Teorema do valor inicial

Para um sinal causal x (n), o teorema do valor inicial afirma que

$ x (0) = \ lim_ {z \ to \ infty} ⁡X (z) $

Isso é usado para encontrar o valor inicial do sinal sem tomar a transformada z inversa

Teorema do valor final

Para um sinal causal x (n), o teorema do valor final afirma que

$ x (\ infty) = \ lim_ {z \ to 1} [z-1] ⁡X (z) $

Isso é usado para encontrar o valor final do sinal sem fazer a transformada z inversa.

Região de Convergência (ROC) da Transformada Z

A faixa de variação de z para a qual converge a transformada z é chamada de região de convergência da transformada z.

Propriedades de ROC de Z-Transforms

ROC da transformada z é indicada com um círculo no plano z.
ROC não contém nenhum pólo.
Se x (n) é uma sequência causal de duração finita ou sequência do lado direito, então o ROC é todo o plano z exceto em z = 0.
Se x (n) é uma sequência anti-causal de duração finita ou sequência do lado esquerdo, então o ROC é todo o plano z exceto em z = ∞.
Se x (n) é uma sequência causal de duração infinita, ROC é exterior ao círculo com raio aie | z | > a.
Se x (n) é uma sequência anti-causal de duração infinita, ROC é o interior do círculo com raio aie | z | <a.
Se x (n) é uma sequência de dois lados de duração finita, então o ROC é todo o plano z exceto em z = 0 & z = ∞.

O conceito de ROC pode ser explicado pelo seguinte exemplo:

Example 1: Encontre a transformada z e ROC de $ a ^ nu [n] + a ^ {-} nu [-n-1] $

$ ZT [a ^ nu [n]] + ZT [a ^ {- n} u [-n-1]] = {Z \ sobre Za} + {Z \ sobre Z {-1 \ sobre a}} $

$$ ROC: | z | \ gt a \ quad \ quad ROC: | z | \ lt {1 \ sobre a} $$

O gráfico de ROC tem duas condições como a> 1 e a <1, como você não conhece a.

Nesse caso, não há combinação ROC.

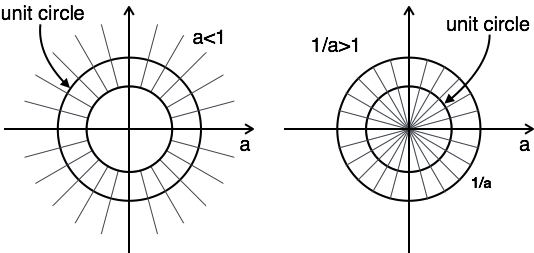
Aqui, a combinação de ROC é de $ a \ lt | z | \ lt {1 \ sobre a} $

Portanto, para este problema, a transformada z é possível quando a <1.

Causalidade e estabilidade

A condição de causalidade para sistemas LTI de tempo discreto é a seguinte:

Um sistema LTI de tempo discreto é causal quando

ROC está fora do pólo externo.
Em A função de transferência H [Z], a ordem do numerador não pode ser maior que a ordem do denominador.

Condição de estabilidade para sistemas LTI de tempo discreto

Um sistema LTI de tempo discreto é estável quando

sua função de sistema H [Z] inclui círculo unitário | z | = 1.
todos os pólos da função de transferência estão dentro do círculo unitário | z | = 1.

Transformada Z de sinais básicos

x (t)	X [Z]
$ \ delta $	1
$ u (n) $	$ {Z \ sobre Z-1} $
$ u (-n-1) $	$ - {Z \ sobre Z-1} $
$ \ delta (nm) $	$ z ^ {- m} $
$ a ^ nu [n] $	$ {Z \ sobre Za} $
$ a ^ nu [-n-1] $	$ - {Z \ sobre Za} $
$ n \, a ^ nu [n] $	$ {aZ \ over \| Za \| ^ 2} $
$ n \, a ^ nu [-n-1] $	$ - {aZ \ over \| Za \| ^ 2} $
$ a ^ n \ cos \ omega nu [n] $	$ {Z ^ 2-aZ \ cos \ omega \ over Z ^ 2-2aZ \ cos \ omega + a ^ 2} $
$ a ^ n \ sin \ omega nu [n] $	$ {aZ \ sin \ omega \ over Z ^ 2 -2aZ \ cos \ omega + a ^ 2} $