Boltzmann Makinesi
Bunlar, tekrarlayan yapıya sahip stokastik öğrenme süreçleridir ve YSA'da kullanılan erken optimizasyon tekniklerinin temelini oluşturur. Boltzmann Makinesi 1985 yılında Geoffrey Hinton ve Terry Sejnowski tarafından icat edildi. Hinton'un Boltzmann Machine hakkındaki sözlerinde daha fazla netlik gözlemlenebilir.
"Bu ağın şaşırtıcı bir özelliği, yalnızca yerel olarak mevcut bilgileri kullanmasıdır. Ağırlık değişimi, değişiklik küresel bir ölçüyü optimize etse de, yalnızca bağlandığı iki birimin davranışına bağlıdır ”- Ackley, Hinton 1985.
Boltzmann Makinesi ile ilgili bazı önemli noktalar -
Tekrarlayan yapı kullanırlar.
1 veya 0 olmak üzere iki olası durumdan birine sahip olan stokastik nöronlardan oluşurlar.
Buradaki nöronların bazıları uyarlanabilir (serbest durum) ve bazıları kenetlenmiş (donmuş durum).
Ayrık Hopfield ağına benzetilmiş tavlama uygularsak, bu Boltzmann Makinesi olur.
Boltzmann Makinasının Amacı
Boltzmann Machine'in temel amacı, bir problemin çözümünü optimize etmektir. Söz konusu problemle ilgili ağırlıkları ve miktarı optimize etmek Boltzmann Machine'in işidir.
Mimari
Aşağıdaki diyagram Boltzmann makinesinin mimarisini göstermektedir. Diyagramdan, iki boyutlu bir birimler dizisi olduğu açıktır. Burada, birimler arasındaki ara bağlantıların ağırlıkları–p nerede p > 0. Kendi kendine bağlantıların ağırlıkları,b nerede b > 0.
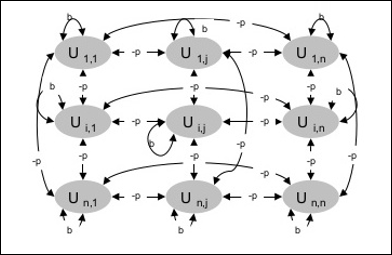
Eğitim Algoritması
Boltzmann makinelerinin sabit ağırlıkları olduğunu bildiğimiz için, ağdaki ağırlıkları güncellememiz gerekmediğinden eğitim algoritması olmayacaktır. Bununla birlikte, ağı test etmek için ağırlıkları ayarlamamız ve fikir birliği işlevini (CF) bulmamız gerekir.
Boltzmann makinesi bir dizi üniteye sahiptir Ui ve Uj ve üzerlerinde çift yönlü bağlantılar vardır.
Sabit ağırlığı düşünüyoruz diyelim wij.
wij ≠ 0 Eğer Ui ve Uj bağlılar.
Ağırlıklı ara bağlantıda da bir simetri vardır, yani wij = wji.
wii ayrıca vardır, yani birimler arasında kendi kendine bağlantı olacaktır.
Herhangi bir birim için Ui, durumu ui 1 veya 0 olur.
Boltzmann Makinesinin temel amacı, aşağıdaki ilişki ile verilebilecek Mutabakat Fonksiyonunu (CF) maksimize etmektir.
$$ CF \: = \: \ displaystyle \ sum \ limits_ {i} \ displaystyle \ sum \ limits_ {j \ leqslant i} w_ {ij} u_ {i} u_ {j} $$
Şimdi, durum 1'den 0'a veya 0'dan 1'e değiştiğinde, fikir birliğindeki değişiklik aşağıdaki ilişki ile verilebilir:
$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$
Buraya ui şu anki durumu Ui.
Katsayıdaki değişim (1 - 2ui) aşağıdaki ilişki ile verilir -
$$ (1 \: - \: 2u_ {i}) \: = \: \ begin {case} +1 ve U_ {i} \: eşittir \: şu anda \: off \\ - 1, & U_ {i } \: şu anda \: üzerinde \ end {case} $$
Genel olarak birim Uidurumunu değiştirmez, ancak değiştirirse, bilgi birim için yerel olarak ikamet ediyor olacaktır. Bu değişiklikle, ağın fikir birliğinde de bir artış olacaktı.
Şebekenin, birimin durumundaki değişikliği kabul etme olasılığı aşağıdaki ilişki ile verilmektedir:
$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$
Buraya, Tkontrol eden parametredir. CF maksimum değere ulaştıkça azalacaktır.
Test Algoritması
Step 1 - Eğitimi başlatmak için aşağıdakileri başlatın -
- Problemin kısıtlamasını temsil eden ağırlıklar
- Kontrol Parametresi T
Step 2 - Durdurma koşulu doğru olmadığında 3-8 adımlarına devam edin.
Step 3 - Adım 4-7'yi gerçekleştirin.
Step 4 - Eyaletlerden birinin ağırlığı değiştirdiğini varsayın ve tamsayıyı seçin I, J rastgele değerler olarak 1 ve n.
Step 5 - Fikir birliğindeki değişikliği aşağıdaki gibi hesaplayın -
$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$
Step 6 - Bu ağın durumdaki değişikliği kabul etme olasılığını hesaplayın
$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$
Step 7 - Bu değişikliği aşağıdaki şekilde kabul edin veya reddedin -
Case I - eğer R < AFdeğişikliği kabul edin.
Case II - eğer R ≥ AF, değişikliği reddedin.
Buraya, R 0 ile 1 arasındaki rastgele sayıdır.
Step 8 - Kontrol parametresini (sıcaklık) aşağıdaki şekilde azaltın -
T(new) = 0.95T(old)
Step 9 - Aşağıdaki gibi olabilecek durdurma koşullarını test edin -
- Sıcaklık belirli bir değere ulaştı
- Belirli sayıda yineleme için durumda değişiklik yok