Vektör Nicemlemeyi Öğrenme
Vektör Nicemleme (LVQ), Vektör nicemleme (VQ) ve Kohonen Kendi Kendini Düzenleyen Haritalardan (KSOM) farklı olarak, temelde denetimli öğrenmeyi kullanan rekabetçi bir ağdır. Bunu, her çıktı biriminin bir sınıfı temsil ettiği kalıpları sınıflandırma süreci olarak tanımlayabiliriz. Denetimli öğrenmeyi kullandığı için, ağa, çıktı sınıfının ilk dağıtımı ile birlikte bilinen sınıflandırmaya sahip bir dizi eğitim modeli verilecektir. Eğitim sürecini tamamladıktan sonra, LVQ bir girdi vektörünü çıktı birimiyle aynı sınıfa atayarak sınıflandıracaktır.
Mimari
Aşağıdaki şekil, KSOM mimarisine oldukça benzeyen LVQ mimarisini göstermektedir. Gördüğümüz gibi var“n” giriş birimi sayısı ve “m”çıktı birimlerinin sayısı. Katmanlar, üzerlerinde ağırlıklarla tamamen birbirine bağlıdır.

Kullanılan Parametreler
LVQ eğitim sürecinde ve akış şemasında kullanılan parametreler aşağıdadır.
x= eğitim vektörü (x 1 , ..., x i , ..., x n )
T = eğitim vektörü için sınıf x
wj = ağırlık vektörü jth çıktı ünitesi
Cj = ile ilişkili sınıf jth çıktı ünitesi
Eğitim Algoritması
Step 1 - Aşağıdaki gibi yapılabilen referans vektörlerini başlatın -
Step 1(a) - Verilen eğitim vektörlerinden ilkini alın "m”(Küme sayısı) eğitim vektörleri ve bunları ağırlık vektörleri olarak kullanın. Kalan vektörler eğitim için kullanılabilir.
Step 1(b) - İlk ağırlığı ve sınıflandırmayı rastgele atayın.
Step 1(c) - K-ortalamalı kümeleme yöntemini uygulayın.
Step 2 - $ \ alpha $ referans vektörünü başlat
Step 3 - Bu algoritmayı durdurma koşulu karşılanmazsa 4-9. Adımlarla devam edin.
Step 4 - Her eğitim giriş vektörü için 5-6 arası adımları izleyin x.
Step 5 - Öklid Mesafesinin Karesini Hesapla j = 1 to m ve i = 1 to n
$$ D (j) \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$
Step 6 - Kazanan birimi edinin J nerede D(j) minimumdur.
Step 7 - Kazanan birimin yeni ağırlığını aşağıdaki ilişkiye göre hesaplayın -
Eğer T = Cj sonra $ w_ {j} (yeni) \: = \: w_ {j} (eski) \: + \: \ alpha [x \: - \: w_ {j} (eski)] $
Eğer T ≠ Cj sonra $ w_ {j} (yeni) \: = \: w_ {j} (eski) \: - \: \ alpha [x \: - \: w_ {j} (eski)] $
Step 8 - $ \ alpha $ öğrenme oranını azaltın.
Step 9- Durdurma koşulunu test edin. Aşağıdaki gibi olabilir -
- Maksimum dönem sayısına ulaşıldı.
- Öğrenme oranı ihmal edilebilir bir değere indirildi.
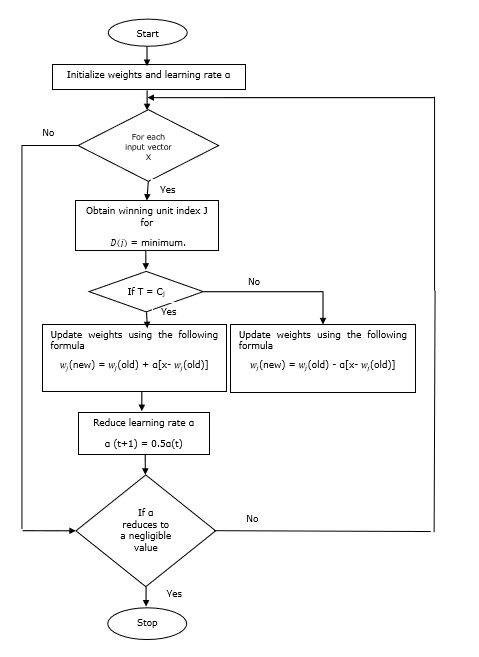
Akış çizelgesi
Varyantlar
Kohonen tarafından LVQ2, LVQ2.1 ve LVQ3 adlı diğer üç değişken geliştirilmiştir. Kazanan ve ikinci ünitenin öğreneceği konsept nedeniyle tüm bu üç varyanttaki karmaşıklık, LVQ'dan daha fazladır.
LVQ2
Yukarıda tartışıldığı gibi, LVQ'nun diğer varyantlarının kavramı, LVQ2'nin durumu pencere tarafından oluşturulur. Bu pencere aşağıdaki parametrelere dayalı olacaktır -
x - mevcut giriş vektörü
yc - en yakın referans vektörü x
yr - sonraki en yakın diğer referans vektörü x
dc - uzaklık x -e yc
dr - uzaklık x -e yr
Giriş vektörü x pencereye düşerse
$$ \ frac {d_ {c}} {d_ {r}} \:> \: 1 \: - \: \ theta \: \: ve \: \: \ frac {d_ {r}} {d_ {c }} \:> \: 1 \: + \: \ theta $$
Burada $ \ theta $, eğitim örneklerinin sayısıdır.
Güncelleme aşağıdaki formül ile yapılabilir -
$ y_ {c} (t \: + \: 1) \: = \: y_ {c} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c} (t)] $ (belongs to different class)
$ y_ {r} (t \: + \: 1) \: = \: y_ {r} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {r} (t)] $ (belongs to same class)
Burada $ \ alpha $ öğrenme oranıdır.
LVQ2.1
LVQ2.1'de, en yakın iki vektörü alacağız: yc1 ve yc2 ve pencere koşulu aşağıdaki gibidir -
$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) $$
$$ Max \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \: <\ :( 1 \ : + \: \ theta) $$
Güncelleme aşağıdaki formül ile yapılabilir -
$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)
$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)
Burada $ \ alpha $ öğrenme oranıdır.
LVQ3
LVQ3'te, en yakın iki vektörü alacağız: yc1 ve yc2 ve pencere koşulu aşağıdaki gibidir -
$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) (1 \: + \: \ theta) $$
Burada $ \ theta \ yaklaşık 0.2 $
Güncelleme aşağıdaki formül ile yapılabilir -
$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)
$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)
Burada $ \ beta $, $ \ alpha $ öğrenme oranının katıdır ve $\beta\:=\:m \alpha(t)$ her biri için 0.1 < m < 0.5