Yapay Sinir Ağı - Hopfield Ağları
Hopfield sinir ağı, 1982 yılında Dr. John J. Hopfield tarafından icat edildi. Bir veya daha fazla tamamen bağlı tekrarlayan nöron içeren tek bir katmandan oluşur. Hopfield ağı, genellikle otomatik ilişkilendirme ve optimizasyon görevleri için kullanılır.
Ayrık Hopfield Ağı
Ayrık bir çizgi biçiminde çalışan veya başka bir deyişle, giriş ve çıkış modellerinin doğada ikili (0,1) veya iki kutuplu (+1, -1) olabilen ayrık vektörler olduğu söylenebilir. Ağ, kendi kendine bağlantıları olmayan simetrik ağırlıklara sahiptir, yani,wij = wji ve wii = 0.
Mimari
Ayrı Hopfield ağı hakkında akılda tutulması gereken bazı önemli noktalar şunlardır:
Bu model, bir ters çeviren ve bir ters çevirmeyen çıktıya sahip nöronlardan oluşur.
Her bir nöronun çıktısı, diğer nöronların girdisi olmalı ama benliğin girdisi olmamalıdır.
Ağırlık / bağlantı gücü şu şekilde temsil edilir: wij.
Bağlantılar hem uyarıcı hem de inhibe edici olabilir. Nöronun çıktısı girdiyle aynıysa uyarıcı, aksi takdirde engelleyici olur.
Ağırlıklar simetrik olmalıdır, yani wij = wji
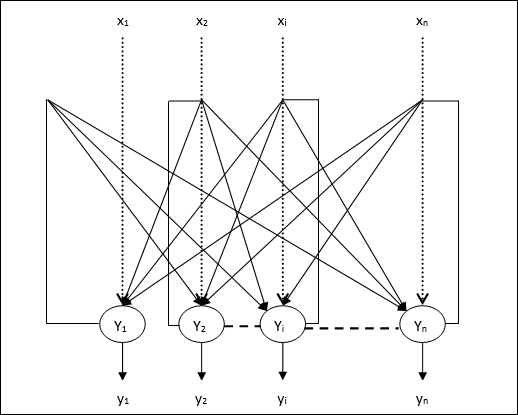
Çıkış Y1 gidiyor Y2, Yi ve Yn ağırlıklara sahip olmak w12, w1i ve w1nsırasıyla. Benzer şekilde, diğer yayların üzerinde de ağırlık vardır.
Eğitim Algoritması
Ayrı Hopfield ağının eğitimi sırasında ağırlıklar güncellenecektir. Bildiğimiz gibi ikili giriş vektörlerinin yanı sıra iki kutuplu giriş vektörlerine de sahip olabiliriz. Dolayısıyla her iki durumda da ağırlık güncellemeleri aşağıdaki ilişki ile yapılabilir.
Case 1 - İkili giriş modelleri
Bir dizi ikili desen için s(p), p = 1 to P
Buraya, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Ağırlık Matrisi şu şekilde verilir:
$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [2s_ {i} (p) - \: 1] [2s_ {j} (p) - \: 1] \: \: \: \: \: için \: i \: \ neq \: j $$
Case 2 - Bipolar giriş kalıpları
Bir dizi ikili desen için s(p), p = 1 to P
Buraya, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Ağırlık Matrisi şu şekilde verilir:
$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [s_ {i} (p)] [s_ {j} (p)] \: \: \: \: \: için \ : i \: \ neq \: j $$
Test Algoritması
Step 1 - Hebbian prensibini kullanarak eğitim algoritmasından elde edilen ağırlıkları başlatın.
Step 2 - Ağ etkinleştirmeleri birleştirilmediyse 3-9 arasındaki adımları uygulayın.
Step 3 - Her giriş vektörü için X4-8. adımları gerçekleştirin.
Step 4 - Ağın ilk aktivasyonunu harici giriş vektörüne eşit yapın X aşağıdaki gibi -
$$ y_ {i} \: = \: x_ {i} \: \: \: için \: i \: = \: 1 \: - \: n $$
Step 5 - Her birim için Yi6-9 arası adımları gerçekleştirin.
Step 6 - Ağın net girişini aşağıdaki şekilde hesaplayın -
$$ y_ {ini} \: = \: x_ {i} \: + \: \ displaystyle \ sum \ limits_ {j} y_ {j} w_ {ji} $$
Step 7 - Çıkışı hesaplamak için etkinleştirmeyi aşağıdaki şekilde net girdiye uygulayın -
$$ y_ {i} \: = \ start {case} 1 & if \: y_ {ini} \:> \: \ theta_ {i} \\ y_ {i} & if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 & if \: y_ {ini} \: <\: \ theta_ {i} \ end {case} $$
Burada $ \ theta_ {i} $ eşiktir.
Step 8 - Bu çıktıyı yayınla yi diğer tüm birimlere.
Step 9 - Ağı bağlantı için test edin.
Enerji Fonksiyonu Değerlendirmesi
Enerji fonksiyonu, sistemin durumunun bağlı ve artmayan fonksiyonu olarak tanımlanır.
Enerji fonksiyonu Ef, ayrıca denir Lyapunov function ayrık Hopfield ağının kararlılığını belirler ve aşağıdaki gibi karakterize edilir -
$$ E_ {f} \: = \: - \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ n y_ {i} y_ {j} w_ {ij} \: - \: \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} y_ {i} \: + \: \ displaystyle \ sum \ limits_ {i = 1} ^ n \ theta_ {i} y_ {i} $$
Condition - Kararlı bir ağda, düğümün durumu her değiştiğinde, yukarıdaki enerji işlevi azalacaktır.
Varsayalım ki düğüm i durumu $ y_i ^ {(k)} $ 'dan $ y_i ^ {(k \: + \: 1)} $ 'e değiştirdikten sonra Enerji değişimi $ \ Delta E_ {f} $ aşağıdaki ilişki ile verilir
$$ \ Delta E_ {f} \: = \: E_ {f} (y_i ^ {(k + 1)}) \: - \: E_ {f} (y_i ^ {(k)}) $$
$$ = \: - \ left (\ begin {dizi} {c} \ displaystyle \ sum \ limits_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \: + \: x_ {i} \: - \: \ theta_ {i} \ end {dizi} \ sağ) (y_i ^ {(k + 1)} \: - \: y_i ^ {(k)}) $$
$$ = \: - \ :( net_ {i}) \ Delta y_ {i} $$
Burada $ \ Delta y_ {i} \: = \: y_i ^ {(k \: + \: 1)} \: - \: y_i ^ {(k)} $
Enerjideki değişim, aynı anda sadece bir birimin aktivasyonunu güncelleyebilmesine bağlıdır.
Sürekli Hopfield Ağı
Kesikli Hopfield ağına kıyasla, sürekli ağın sürekli bir değişken olarak zamanı vardır. Seyahat eden satıcı problemi gibi otomatik ilişkilendirme ve optimizasyon problemlerinde de kullanılır.
Model - Model veya mimari, giriş voltajını bir sigmoid aktivasyon işlevi üzerinden çıkış voltajına eşleyebilen amplifikatörler gibi elektrikli bileşenler eklenerek oluşturulabilir.
Enerji Fonksiyonu Değerlendirmesi
$$ E_f = \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} - \ displaystyle \ sum \ limits_ {i = 1} ^ n x_i y_i + \ frac {1} {\ lambda} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {- 1} (y) dy $$
Buraya λ kazanç parametresidir ve gri giriş iletkenliği.