Öğrenme ve Uyum
Daha önce belirtildiği gibi, YSA tamamen biyolojik sinir sisteminin, yani insan beyninin çalışma biçiminden esinlenmiştir. İnsan beyninin en etkileyici özelliği öğrenmesidir, dolayısıyla aynı özellik YSA tarafından da kazanılmıştır.
YSA'da Öğrenme Nedir?
Temel olarak öğrenme, çevrede bir değişiklik olduğu gibi ve olduğu zaman değişimi de kendi içinde yapmak ve uyarlamak demektir. YSA karmaşık bir sistemdir veya daha doğrusu içinden geçen bilgiye göre iç yapısını değiştirebilen karmaşık bir adaptif sistemdir diyebiliriz.
Neden Önemlidir?
Karmaşık bir uyarlanabilir sistem olan YSA'da öğrenme, bir işlem biriminin ortamdaki değişiklik nedeniyle girdi / çıktı davranışını değiştirebileceğini ifade eder. YSA'da öğrenmenin önemi, sabit aktivasyon işlevi ve belirli bir ağ kurulduğunda giriş / çıkış vektörü nedeniyle artar. Şimdi girdi / çıktı davranışını değiştirmek için ağırlıkları ayarlamamız gerekiyor.
Sınıflandırma
Aynı sınıfların örnekleri arasında ortak özellikler bularak örneklerin verilerini farklı sınıflara ayırmayı öğrenme süreci olarak tanımlanabilir. Örneğin, YSA eğitimini gerçekleştirmek için benzersiz özelliklere sahip bazı eğitim örneklerimiz var ve testlerini gerçekleştirmek için diğer benzersiz özelliklere sahip bazı test örneklerimiz var. Sınıflandırma, denetimli öğrenmeye bir örnektir.
Sinir Ağı Öğrenme Kuralları
YSA öğrenimi sırasında girdi / çıktı davranışını değiştirmek için ağırlıkları ayarlamamız gerektiğini biliyoruz. Bu nedenle, ağırlıkların değiştirilebileceği bir yöntem gereklidir. Bu yöntemlere, basit algoritmalar veya denklemler olan Öğrenme kuralları adı verilir. Sinir ağı için bazı öğrenme kuralları aşağıdadır -
Hebbian Öğrenme Kuralı
En eski ve en basit kurallardan biri olan bu kural, Donald Hebb tarafından 1949'da The Organization of Behavior adlı kitabında tanıtıldı . Bu bir tür ileri beslemeli, denetimsiz öğrenmedir.
Basic Concept - Bu kural, Hebb tarafından verilen bir öneriye dayanmaktadır, o da -
“A hücresinin bir aksonu, bir B hücresini uyaracak kadar yakın olduğunda ve tekrar tekrar veya ısrarla ateşlemede yer aldığında, B'yi ateşleyen hücrelerden biri olarak A'nın etkinliğini sağlayacak şekilde bir veya iki hücrede bir miktar büyüme süreci veya metabolik değişim gerçekleşir. , artar. "
Yukarıdaki varsayımdan, nöronlar aynı anda ateşlenirse iki nöron arasındaki bağlantıların güçlenebileceği ve farklı zamanlarda ateşlenirse zayıflayabileceği sonucuna varabiliriz.
Mathematical Formulation - Hebbian öğrenme kuralına göre, her adımda bağlantının ağırlığını artırmak için formül aşağıdadır.
$$ \ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t) $$
Burada, $ \ Delta w_ {ji} (t) $ = zaman adımında bağlantının ağırlığının arttığı artış t
$ \ alpha $ = pozitif ve sabit öğrenme oranı
$ x_ {i} (t) $ = zaman adımında sinaptik öncesi nöronun giriş değeri t
$ y_ {i} (t) $ = aynı zamanda adımda sinaptik öncesi nöronun çıktısı t
Perceptron Öğrenme Kuralı
Bu kural, Rosenblatt tarafından sunulan, doğrusal etkinleştirme işlevine sahip tek katmanlı ileri beslemeli ağların denetimli öğrenme algoritmasını düzelten bir hatadır.
Basic Concept- Doğası gereği denetlendiğinden, hatayı hesaplamak için, istenen / hedef çıktı ile gerçek çıktı arasında bir karşılaştırma yapılacaktır. Herhangi bir fark bulunursa bağlantı ağırlıklarında değişiklik yapılmalıdır.
Mathematical Formulation - Matematiksel formülasyonunu açıklamak için, 'n' sayıda sonlu girdi vektörümüz olduğunu varsayalım, x (n) ve bunun istenen / hedef çıktı vektörü t (n) ile birlikte, burada n = 1'den N'ye.
Şimdi, çıktı 'y', daha önce net girdiye göre açıklandığı gibi hesaplanabilir ve bu net girdiye uygulanan aktivasyon fonksiyonu aşağıdaki gibi ifade edilebilir -
$$ y \: = \: f (y_ {in}) \: = \: \ begin {case} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ theta \ end {case} $$
Nerede θ eşiktir.
Ağırlığın güncellenmesi aşağıdaki iki durumda yapılabilir -
Case I - ne zaman t ≠ y, sonra
$$ w (yeni) \: = \: w (eski) \: + \; tx $$
Case II - ne zaman t = y, sonra
Ağırlıkta değişiklik yok
Delta Öğrenme Kuralı (Widrow-Hoff Kuralı)
Tüm eğitim modellerinde hatayı en aza indirmek için, Bernard Widrow ve Marcian Hoff tarafından, En Az Ortalama Kareler (LMS) yöntemi olarak da adlandırılır. Sürekli aktivasyon işlevine sahip bir tür denetimli öğrenme algoritmasıdır.
Basic Concept- Bu kuralın temeli, sonsuza kadar devam eden gradyan-iniş yaklaşımıdır. Delta kuralı, çıktı birimine ve hedef değere net girdiyi en aza indirgemek için sinaptik ağırlıkları günceller.
Mathematical Formulation - Sinaptik ağırlıkları güncellemek için delta kuralı şu şekilde verilir:
$$ \ Delta w_ {i} \: = \: \ alpha \ :. x_ {i} .e_ {j} $$
Burada $ \ Delta w_ {i} $ = i th pattern için ağırlık değişimi ;
$ \ alpha $ = pozitif ve sabit öğrenme oranı;
$ x_ {i} $ = sinaptik öncesi nöronun giriş değeri;
$ e_ {j} $ = $ (t \: - \: y_ {in}) $, istenen / hedef çıktı ile gerçek çıktı arasındaki fark $ y_ {in} $
Yukarıdaki delta kuralı yalnızca tek bir çıktı birimi içindir.
Ağırlığın güncellenmesi aşağıdaki iki durumda yapılabilir -
Case-I - ne zaman t ≠ y, sonra
$$ w (yeni) \: = \: w (eski) \: + \: \ Delta w $$
Case-II - ne zaman t = y, sonra
Ağırlıkta değişiklik yok
Rekabetçi Öğrenme Kuralı (Kazanan her şeyi alır)
Çıkış düğümlerinin giriş modelini temsil etmek için birbirleriyle rekabet etmeye çalıştıkları denetimsiz eğitimle ilgilidir. Bu öğrenme kuralını anlamak için, aşağıdaki gibi verilen rekabetçi ağı anlamalıyız -
Basic Concept of Competitive Network- Bu ağ, çıkışlar arasında geri besleme bağlantısı olan tek katmanlı ileri beslemeli bir ağ gibidir. Çıkışlar arasındaki bağlantılar engelleyici tiptedir ve noktalı çizgilerle gösterilir, bu da rakiplerin asla kendilerini desteklemeyecekleri anlamına gelir.
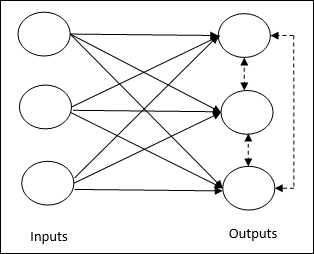
Basic Concept of Competitive Learning Rule- Daha önce de belirtildiği gibi, çıkış düğümleri arasında bir rekabet olacak. Bu nedenle, ana konsept, eğitim sırasında, belirli bir girdi modeline en yüksek aktivasyona sahip çıktı biriminin kazanan ilan edileceğidir. Bu kurala aynı zamanda Kazanan her şeyi alır, çünkü yalnızca kazanan nöron güncellenir ve nöronların geri kalanı değişmeden kalır.
Mathematical formulation - Bu öğrenme kuralının matematiksel formülasyonu için üç önemli faktör aşağıdadır -
Condition to be a winner - Diyelim ki bir nöron $ y_ {k} $ kazanan olmak istiyorsa, aşağıdaki koşul ortaya çıkacaktır -
$$ y_ {k} \: = \: \ start {case} 1 & if \: v_ {k} \:> \: v_ {j} \: for \: all \: j, \: j \: \ neq \: k \\ 0 & aksi halde \ end {case} $$
Bunun anlamı, eğer $ y_ {k} $ diyelim ki herhangi bir nöron kazanmak istiyorsa, indüklenmiş yerel alanı (toplama biriminin çıktısı), diyelim ki $ v_ {k} $, diğer tüm nöronlar arasında en büyüğü olmalıdır. ağda.
Condition of sum total of weight - Rekabetçi öğrenme kuralı üzerindeki diğer bir kısıtlama, belirli bir çıkış nöronunun ağırlıklarının toplamının 1 olacağıdır. Örneğin, nöronu düşünürsek k sonra -
$$ \ displaystyle \ sum \ limits_ {j} w_ {kj} \: = \: 1 \: \: \: \: \: \: \: \: \: for \: all \: k $$
Change of weight for winner- Bir nöron giriş modeline yanıt vermezse, o nöronda hiçbir öğrenme gerçekleşmez. Bununla birlikte, belirli bir nöron kazanırsa, ilgili ağırlıklar aşağıdaki gibi ayarlanır
$$ \ Delta w_ {kj} \: = \: \ begin {case} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0, & if \: nöron \: k \: kayıplar \ end {vakalar} $$
Burada $ \ alpha $ öğrenme oranıdır.
Bu, ağırlığını ayarlayarak kazanan nöronu tercih ettiğimizi ve eğer bir nöron kaybı varsa, ağırlığını yeniden ayarlamak için uğraşmamıza gerek olmadığını açıkça gösteriyor.
Outstar Öğrenme Kuralı
Grossberg tarafından getirilen bu kural, istenen çıktılar bilindiğinden denetimli öğrenmeyle ilgilidir. Aynı zamanda Grossberg öğrenimi olarak da adlandırılır.
Basic Concept- Bu kural, bir katman halinde düzenlenmiş nöronlar üzerine uygulanır. İstenilen çıktıyı üretmek için özel olarak tasarlanmıştır.d katmanının p nöronlar.
Mathematical Formulation - Bu kuraldaki ağırlık ayarlamaları aşağıdaki gibi hesaplanır
$$ \ Delta w_ {j} \: = \: \ alpha \ :( d \: - \: w_ {j}) $$
Buraya d istenen nöron çıktısı ve $ \ alpha $ öğrenme oranıdır.