Hopfield Ağını Kullanarak Optimizasyon
Optimizasyon, tasarım, durum, kaynak ve sistem gibi bir şeyi olabildiğince etkili hale getirme eylemidir. Maliyet fonksiyonu ile enerji fonksiyonu arasındaki benzerliği kullanarak, optimizasyon problemlerini çözmek için birbiriyle oldukça bağlantılı nöronları kullanabiliriz. Böyle bir tür sinir ağı, bir veya daha fazla tamamen bağlı tekrarlayan nöron içeren tek bir katmandan oluşan Hopfield ağıdır. Bu, optimizasyon için kullanılabilir.
Optimizasyon için Hopfield ağını kullanırken hatırlanması gereken noktalar -
Enerji işlevi ağın minimum olması gerekir.
Depolanan modellerden birini seçmek yerine tatmin edici bir çözüm bulacaktır.
Hopfield ağı tarafından bulunan çözümün kalitesi, ağın başlangıç durumuna önemli ölçüde bağlıdır.
Seyahat Eden Satıcı Problemi
Satıcının gittiği en kısa yolu bulmak, Hopfield sinir ağı kullanılarak optimize edilebilen hesaplama problemlerinden biridir.
TSP'nin Temel Kavramı
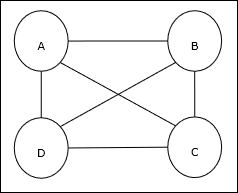
Seyahat Eden Satıcı Problemi (TSP), bir satıcının seyahat etmek zorunda olduğu klasik bir optimizasyon problemidir. nBirbirleriyle bağlantılı şehirler, maliyeti ve gidilen mesafeyi minimumda tutuyor. Örneğin, satıcı A, B, C, D 4 şehirden oluşan bir sette seyahat etmek zorundadır ve amaç, en kısa döngüsel tur olan ABC-D'yi bulmaktır, bu da maliyeti en aza indirgemek için, son şehir D'den ilk şehir A'ya
Matris Gösterimi
Aslında her n-city TSP turu şu şekilde ifade edilebilir: n × n matris kimin ith satır açıklar ithşehrin konumu. Bu matris,M4 şehir için A, B, C, D şu şekilde ifade edilebilir -
$$ M = \ başla {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 ve 0 ve 1 \ end {bmatrix} $$
Hopfield Ağı Çözümleri
Bu TSP'nin Hopfield ağı tarafından çözümü düşünülürken, ağdaki her düğüm matristeki bir öğeye karşılık gelir.
Enerji Fonksiyonu Hesaplaması
Optimize edilmiş çözüm olmak için enerji işlevi minimum olmalıdır. Aşağıdaki kısıtlamalar temelinde enerji fonksiyonunu şu şekilde hesaplayabiliriz:
Kısıtlama-I
Temelde enerji fonksiyonunu hesaplayacağımız ilk kısıt, her bir matris satırında bir öğenin 1'e eşit olması gerektiğidir. M ve her satırdaki diğer öğeler şuna eşit olmalıdır: 0çünkü her şehir TSP turunda sadece bir konumda gerçekleşebilir. Bu kısıtlama matematiksel olarak şu şekilde yazılabilir -
$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: \: \ lbrace1, ..., n \ rbrace $ içinde \: x \: \ için $
Şimdi, yukarıdaki kısıtlamaya dayalı olarak minimize edilecek enerji fonksiyonu, - ile orantılı bir terim içerecektir.
$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j } \ end {dizi} \ sağ) ^ 2 $$
Kısıtlama-II
Bildiğimiz gibi, TSP'de bir şehir turun herhangi bir konumunda olabilir, dolayısıyla her bir matris sütununda M, bir eleman 1'e ve diğer elemanlar 0'a eşit olmalıdır. Bu kısıt matematiksel olarak aşağıdaki gibi yazılabilir -
$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: \: \ lbrace1, ..., n \ rbrace $ için \: j \: \ için $
Şimdi, yukarıdaki kısıtlamaya dayalı olarak minimize edilecek enerji fonksiyonu, - ile orantılı bir terim içerecektir.
$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j } \ end {dizi} \ sağ) ^ 2 $$
Maliyet Fonksiyonu Hesaplama
Diyelim ki bir kare matris (n × n) ile gösterilir C TSP'nin maliyet matrisini gösterir. n nerede şehirler n > 0. Maliyet fonksiyonu hesaplanırken kullanılan bazı parametreler aşağıdadır -
Cx, y - Maliyet matrisi unsuru, şehirden seyahat etmenin maliyetini gösterir x -e y.
A ve B öğelerinin bitişikliği aşağıdaki ilişki ile gösterilebilir:
$$ M_ {x, i} \: = \: 1 \: \: ve \: \: M_ {y, i \ pm 1} \: = \: 1 $$
Bildiğimiz gibi, Matrix'te her düğümün çıktı değeri 0 veya 1 olabilir, dolayısıyla her A, B şehir çifti için enerji fonksiyonuna aşağıdaki terimleri ekleyebiliriz -
$$ \ displaystyle \ toplam \ limitler_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$
Yukarıdaki maliyet fonksiyonu ve kısıtlama değeri temelinde, son enerji fonksiyonu E aşağıdaki gibi verilebilir -
$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {x} \ displaystyle \ sum \ limits_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$
$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limits_ {x} \ left (\ begin {dizi} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {i} M_ {x, i} \ end {dizi} \ sağ) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limits_ {i} \ left (\ begin {dizi} {c} 1 \: - \ : \ displaystyle \ sum \ limits_ {x} M_ {x, i} \ end {dizi} \ sağ) ^ 2 \ end {bmatrix} $$
Buraya, γ1 ve γ2 iki tartım sabitidir.