Onaltılık Aritmetik
Onaltılık Sayı Sistemi
Aşağıda onaltılık sayı sisteminin özellikleri verilmiştir.
10 basamak ve 6 harf kullanır, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.
Harfler 10'dan başlayan sayıları temsil eder. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
16 tabanlı sayı sistemi olarak da adlandırılır.
Onaltılık sayıdaki her pozisyon, tabanın (16) 0 kuvvetini temsil eder. Örnek - 16 0
Onaltılık bir sayıdaki son konum, tabanın (16) x üssünü temsil eder. Örnek - 16 x burada x son konumu temsil eder - 1.
Misal
Onaltılık Sayı - 19FDE 16
Ondalık Eşdeğeri Hesaplanıyor -
| Adım | Onaltılık Sayı | Ondalık sayı |
|---|---|---|
| Aşama 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| Adım 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| Aşama 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| 4. adım | 19FDE 16 | 106462 10 |
Note −19FDE 16 normalde 19FDE olarak yazılır.
Onaltılık Toplama
Aşağıdaki onaltılık toplama tablosu, Onaltılık toplamayı işlemenize büyük ölçüde yardımcı olacaktır.
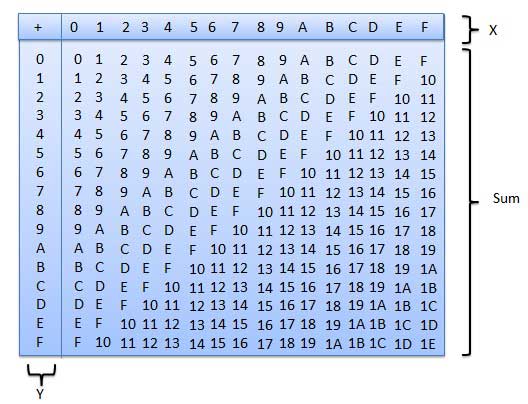
Bu tabloyu kullanmak için, bu örnekte kullanılan talimatları izleyin - A 16 ve 5 16 ekleyin . X sütununda A'yı bulun ve ardından Y sütununda 5'i bulun. Bu iki sütunun kesiştiği 'toplam' alanındaki nokta, iki sayının toplamıdır.
A16 + 516 = F16.Örnek - Toplama
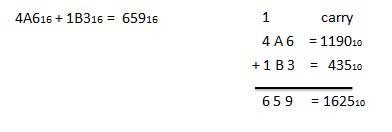
Onaltılık Çıkarma
Onaltılık sayıların çıkarılması, diğer herhangi bir sayı sistemindeki sayıların çıkarılmasıyla aynı kuralları izler. Tek varyasyon ödünç alınan sayıdadır. Ondalık sistemde, 10 10'luk bir grup ödünç alırsınız . İkili sistemde, 2 10 kişilik bir grup ödünç alırsınız . Onaltılık sistemde 16 10 kişilik bir grup ödünç alırsınız .
Örnek - Çıkarma
