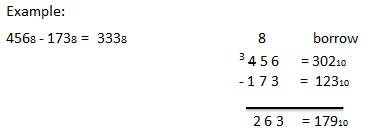Sekizli Aritmetik
Sekizli Sayı Sistemi
Aşağıda sekizlik sayı sisteminin özellikleri verilmiştir.
Sekiz basamaklı 0,1,2,3,4,5,6,7 kullanır.
8 tabanlı sayı sistemi olarak da adlandırılır.
Sekizlik bir sayıdaki her konum, tabanın (8) 0 kuvvetini temsil eder. Örnek: 8 0
Sekizlik bir sayıdaki son konum, tabanın (8) x kuvvetini temsil eder. Örnek: 8 x burada x son konumu temsil eder - 1.
Misal
Sekizli Sayı - 12570 8
Ondalık Eşdeğeri Hesaplanıyor -
| Adım | Sekizli Sayı | Ondalık sayı |
|---|---|---|
| Aşama 1 | 12570 8 | ((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10 |
| Adım 2 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| Aşama 3 | 12570 8 | 5496 10 |
Note −12570 8 , normalde 12570 olarak yazılır.
Sekizli Toplama
Aşağıdaki sekizlik toplama tablosu, sekizli toplamayı işlemenize yardımcı olacaktır.

Bu tabloyu kullanmak için, bu örnekte kullanılan talimatları izleyin: 6 8 ve 5 8'i ekleyin . A sütununda 6'yı bulun ve ardından B sütununda 5'i bulun. Bu iki sütunun kesiştiği 'toplam' alanındaki nokta, iki sayının 'toplamı'dır.
68 + 58 = 138.Örnek - Toplama
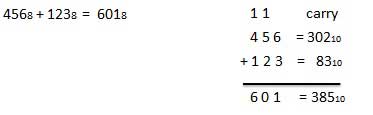
Sekizli Çıkarma
Sekizli sayıların çıkarılması, diğer sayı sistemlerinde sayıların çıkarılmasıyla aynı kuralları izler. Tek varyasyon ödünç alınan sayıdadır. Ondalık sistemde, 10 10'luk bir grup ödünç alırsınız . İkili sistemde, 2 10 kişilik bir grup ödünç alırsınız . Sekizli sistemde 8 10 kişilik bir grup ödünç alırsınız .
Örnek - Çıkarma