Lý thuyết mạng - Mạch ghép nối
Một mạch điện được cho là coupled circuit, khi tồn tại cảm kháng lẫn nhau giữa các cuộn dây (hoặc cuộn cảm) có trong đoạn mạch đó. Cuộn dây không là gì ngoài sự kết hợp nối tiếp của điện trở và cuộn cảm. Trong trường hợp không có điện trở, cuộn dây trở thành cuộn cảm. Đôi khi, thuật ngữ cuộn dây và cuộn cảm được sử dụng thay thế cho nhau.
Trong chương này, trước tiên chúng ta hãy thảo luận về quy ước dấu chấm và sau đó sẽ thảo luận về phân loại ghép nối.
Quy ước chấm
Quy ước chấm là một kỹ thuật, cung cấp các chi tiết về cực tính của điện áp tại đầu cuối có chấm. Thông tin này rất hữu ích khi viết phương trình KVL.
Nếu dòng điện đi vào đầu nối chấm của một cuộn dây (hoặc cuộn cảm), thì nó tạo ra điện áp ở cuộn dây khác (hoặc cuộn cảm), đang có positive polarity tại thiết bị đầu cuối có dấu chấm.
Nếu dòng điện rời khỏi đầu nối chấm của một cuộn dây (hoặc cuộn cảm), thì nó tạo ra điện áp ở cuộn dây khác (hoặc cuộn cảm), đang có negative polarity tại thiết bị đầu cuối có dấu chấm.
Phân loại khớp nối
Chúng tôi có thể phân loại coupling thành hai loại sau.
- Khớp nối điện
- Khớp nối từ tính
Bây giờ, chúng ta hãy thảo luận về từng loại khớp nối một.
Khớp nối điện
Sự ghép nối điện xảy ra, khi tồn tại một physical connectiongiữa hai cuộn dây (hoặc cuộn cảm). Khớp nối này có thể là loại hỗ trợ hoặc loại đối lập. Nó dựa trên việc dòng điện đi vào đầu cuối có chấm hay rời khỏi đầu cuối có chấm.
Khớp nối kiểu trợ giúp
Xét đoạn mạch điện sau đây có hai cuộn cảm mắc nối tiếp với nhau series.
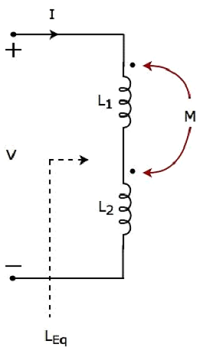
Vì hai cuộn cảm mắc nối tiếp nên same current Ichạy qua hai cuộn cảm có độ tự cảm L 1 và L 2 .
Trong trường hợp này, dòng điện, tôi nhập vào đầu cuối có dấu chấm của mỗi cuộn cảm. Do đó, điện áp cảm ứng trong mỗi cuộn cảm sẽ cópositive polarity ở đầu cuối có chấm do dòng điện chạy trong cuộn dây khác.
Ứng dụng KVL xung quanh vòng dây của mạch điện hoặc mạng điện trên.
$$ V - L_1 \ frac {dI} {dt} - M \ frac {dI} {dt} - L_2 \ frac {dI} {dt} - M \ frac {dI} {dt} = 0 $$
$$ V = L_1 \ frac {dI} {dt} + L_2 \ frac {dI} {dt} + 2M \ frac {dI} {dt} $$
$$ V = (L_1 + L_2 + 2M) \ frac {dI} {dt} $$
Phương trình trên có dạng $ \ mathbf {\ mathit {V = L_ {Eq} \ frac {dI} {dt}}} $
Do đó, equivalent inductance trong số các tổ hợp nối tiếp của cuộn cảm trong hình trên là
$$ L_ {Eq} = L_1 + L_2 + 2 triệu $$
Trong trường hợp này, độ tự cảm tương đương đã được tăng thêm 2M. Do đó, mạch điện trên là một ví dụ vềelectrical khớp nối là của aiding kiểu.
Khớp nối kiểu đối lập
Xét đoạn mạch điện sau đây có hai cuộn cảm mắc nối tiếp với nhau series.
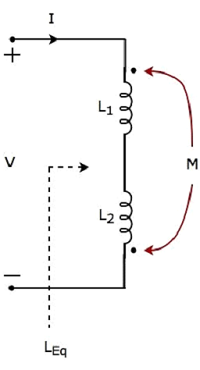
Trong đoạn mạch trên, dòng điện I đi vào đầu cuối có chấm của cuộn cảm có độ tự cảm là L1. Do đó, nó tạo ra một điện áp trong cuộn cảm khác có độ tự cảm làL2. Vì thế,positive polarity của điện áp cảm ứng hiện diện ở đầu nối có chấm của cuộn cảm này.
Trong đoạn mạch trên, dòng điện I rời khỏi đầu cuối có chấm của cuộn cảm có độ tự cảm là L2. Do đó, nó tạo ra một điện áp trong cuộn cảm khác có độ tự cảm làL1. Vì thế,negative polarity của điện áp cảm ứng hiện diện ở đầu nối có chấm của cuộn cảm này.
Ứng dụng KVL xung quanh vòng dây của mạch điện hoặc mạng điện trên.
$$ V - L_1 \ frac {dI} {dt} + M \ frac {dI} {dt} - L_2 \ frac {dI} {dt} + M \ frac {dI} {dt} = 0 $$
$$ \ Rightarrow V = L_1 \ frac {dI} {dt} + L_2 \ frac {dI} {dt} - 2M \ frac {dI} {dt} $$
$$ \ Rightarrow V = (L_1 + L_2 - 2M) \ frac {dI} {dt} $$
Phương trình trên có dạng $ \ mathbf {\ mathit {V = L_ {Eq} \ frac {dI} {dt}}} $
Do đó, equivalent inductance trong số các tổ hợp nối tiếp của cuộn cảm trong hình trên là
$$ L_ {Eq} = L_1 + L_2 - 2 triệu $$
Trong trường hợp này, độ tự cảm tương đương đã giảm đi 2M. Do đó, mạch điện trên là một ví dụ vềelectrical khớp nối là của opposing kiểu.
Khớp nối từ tính
Khớp nối từ tính xảy ra, khi có no physical connectiongiữa hai cuộn dây (hoặc cuộn cảm). Khớp nối này có thể là loại hỗ trợ hoặc loại đối lập. Nó dựa trên việc dòng điện đi vào đầu cuối có chấm hay rời khỏi đầu cuối có chấm.
Khớp nối kiểu trợ giúp
Xem xét điện tương đương sau circuit of transformer. Nó có hai cuộn dây và chúng được gọi là cuộn dây chính và cuộn thứ cấp.
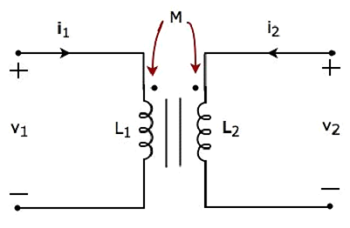
Cường độ dòng điện chạy qua cuộn sơ cấp và cuộn thứ cấp lần lượt là i 1 và i 2 . Trong trường hợp này, các dòng điện nàyentertại đầu cuối có chấm của cuộn dây tương ứng. Do đó, điện áp cảm ứng trong mỗi cuộn dây sẽ có cực tính dương ở đầu nối chấm do dòng điện chạy trong cuộn dây khác.
Ứng dụng KVL xung quanh cuộn sơ cấp.
$$ v_1 - L_1 \ frac {d i_1} {dt} - M \ frac {d i_2} {dt} = 0 $$
$ \ Rightarrow v_1 = L_1 \ frac {d i_1} {dt} + M \ frac {d i_2} {dt} $Equation 1
Ứng dụng KVL xung quanh cuộn thứ cấp.
$$ v_2 - L_2 \ frac {d i_2} {dt} - M \ frac {d i_1} {dt} = 0 $$
$ \ Rightarrow v_2 = L_2 \ frac {d i_2} {dt} + M \ frac {d i_1} {dt} $Equation 2
Trong phương trình 1 và phương trình 2, điện áp tự ngẫu và điện áp cảm ứng biến đổi có cùng cực. Do đó, mạch biến áp trên là một ví dụ vềmagnetic coupling, là của aiding kiểu.
Khớp nối của loại đối lập
Xem xét điện tương đương sau circuit of transformer.

Cường độ dòng điện chạy qua cuộn sơ cấp và cuộn thứ cấp lần lượt là i 1 và i 2 . Trong trường hợp này, dòng điện, i 1 đi vào đầu nối chấm của cuộn sơ cấp. Do đó, nó tạo ra một điện áp trong cuộn thứ cấp. Vì thế,positive polarity của điện áp cảm ứng có ở đầu nối chấm của cuộn thứ cấp này.
Trong đoạn mạch trên, dòng điện, i 2 ra khỏi đầu nối tiếp của cuộn thứ cấp. Do đó, nó tạo ra một điện áp trong cuộn sơ cấp. Vì thế,negative polarity của điện áp cảm ứng hiện diện ở đầu nối chấm của cuộn sơ cấp này.
Ứng dụng KVL xung quanh cuộn sơ cấp.
$$ v_1 - L_1 \ frac {d i_1} {dt} + M \ frac {d i_2} {dt} = 0 $$
$ \ Rightarrow v_1 = L_1 \ frac {d i_1} {dt} - M \ frac {d i_2} {dt} $Equation 3
Ứng dụng KVL xung quanh cuộn thứ cấp.
$$ v_2 - L_2 \ frac {d i_2} {dt} + M \ frac {d i_1} {dt} = 0 $$
$ \ Rightarrow v_2 = L_2 \ frac {d i_2} {dt} - M \ frac {d i_1} {dt} $Equation 4
Trong phương trình 3 và phương trình 4, điện áp tự cảm và điện áp cảm ứng biến đổi có cực tính ngược nhau. Do đó, mạch biến áp trên là một ví dụ vềmagnetic coupling, là của opposing kiểu.