Lý thuyết mạng - Phân tích lưới
Trong phân tích Mesh, chúng ta sẽ xem xét các dòng điện chạy qua mỗi mắt lưới. Do đó, phân tích lưới còn được gọi làMesh-current method.
A branchlà một đường dẫn nối hai nút và nó chứa một phần tử mạch. Nếu một nhánh chỉ thuộc một mắt lưới, thì dòng điện nhánh sẽ bằng dòng điện lưới.
Nếu một nhánh chung cho hai mắt lưới, thì dòng điện nhánh sẽ bằng tổng (hoặc hiệu số) của hai dòng lưới, khi chúng cùng hướng (hoặc ngược chiều).
Quy trình phân tích lưới
Thực hiện theo các bước sau trong khi giải quyết bất kỳ mạng hoặc mạch điện nào bằng cách sử dụng phân tích Mesh.
Step 1 - Xác định meshes và dán nhãn các dòng điện lưới theo chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Step 2 - Quan sát cường độ dòng điện chạy qua từng phần tử về mặt lưới dòng điện.
Step 3 - Viết mesh equationscho tất cả các mắt lưới. Phương trình lưới thu được bằng cách áp dụng KVL đầu tiên và sau đó là định luật Ohm.
Step 4 - Giải các phương trình lưới thu được ở Bước 3 để có được mesh currents.
Bây giờ, chúng ta có thể tìm thấy dòng điện chạy qua bất kỳ phần tử nào và điện áp trên bất kỳ phần tử nào có trong mạng nhất định bằng cách sử dụng dòng điện lưới.
Thí dụ
Tìm hiệu điện thế trên điện trở 30 Ω bằng cách sử dụng Mesh analysis.
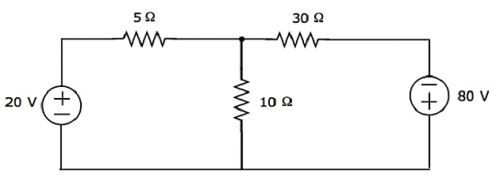
Step 1- Có hai mắt lưới trong đoạn mạch trên. Cácmesh currentsI 1 và I 2 được coi là theo chiều kim đồng hồ. Các dòng điện lưới này được thể hiện trong hình sau.
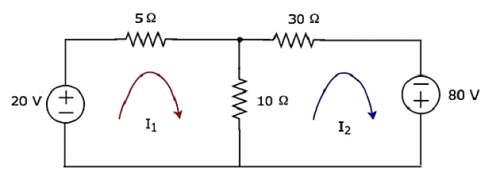
Step 2- Dòng điện lưới I 1 chạy qua nguồn hiệu điện thế 20 V và điện trở 5 Ω. Tương tự, dòng điện lưới I 2 chạy qua điện trở 30 Ω và nguồn điện áp -80 V. Nhưng, sự khác biệt của hai dòng điện lưới, I 1 và I 2 , chạy qua điện trở 10 Ω, vì nó là nhánh chung của hai mắt lưới.
Step 3 - Trong trường hợp này, chúng tôi sẽ nhận được two mesh equationsvì có hai mắt lưới trong mạch đã cho. Khi chúng ta viết phương trình lưới, giả sử dòng điện lưới của mắt lưới cụ thể đó lớn hơn tất cả các dòng điện lưới khác của mạch.
Các mesh equation của lưới đầu tiên là
$$ 20 - 5I_1 -10 (I_1 - I_2) = 0 $$
$$ \ Rightarrow 20 - 15I_1 + 10I_2 = 0 $$
$$ \ Rightarrow 10I_2 = 15I_1 - 20 $$
Chia phương trình trên với 5.
$$ 2I_2 = 3I_1 - 4 $$
Nhân phương trình trên với 2.
4I_2 đô la = 6I_1 - 8 đô la Equation 1
Các mesh equation của lưới thứ hai là
$$ - 10 (I_2 - I_1) - 30I_2 + 80 = 0 $$
Chia phương trình trên với 10.
$$ - (I_2 - I_1) - 3I_2 + 8 = 0 $$
$$ \ Rightarrow -4I_2 + I_1 + 8 = 0 $$
4I_2 đô la = I_1 + 8 đô la Equation 2
Step 4- Tìm dòng lưới I 1 và I 2 bằng cách giải phương trình 1 và phương trình 2.
Các số hạng bên trái của Phương trình 1 và Phương trình 2 giống nhau. Do đó, hãy cân bằng các số hạng bên phải của Phương trình 1 và Phương trình 2 để tìm giá trị của I 1 .
$$ 6I_1 - 8 = I_1 + 8 $$
$$ \ Rightarrow 5I_1 = 16 $$
$$ \ Rightarrow I_1 = \ frac {16} {5} A $$
Thay thế giá trị I 1 trong Công thức 2.
$$ 4I_2 = \ frac {16} {5} + 8 $$
$$ \ Rightarrow 4I_2 = \ frac {56} {5} $$
$$ \ Rightarrow I_2 = \ frac {14} {5} A $$
Vì vậy, chúng tôi nhận được dòng lưới I 1 và I 2 là $ \ mathbf {\ frac {16} {5}} $A và $ \ mathbf {\ frac {14} {5}} $ A tương ứng.
Step 5- Dòng điện chạy qua điện trở 30 Ω không là gì khác ngoài dòng điện lưới I 2 và nó bằng $ \ frac {14} {5} $ A. Bây giờ, chúng ta có thể tìm hiệu điện thế trên điện trở 30 Ω bằng cách sử dụng định luật Ôm.
$$ V_ {30 \ Omega} = I_2 R $$
Thay các giá trị của I 2 và R vào phương trình trên.
$$ V_ {30 \ Omega} = \ lgroup \ frac {14} {5} \ rgroup 30 $$
$$ \ Rightarrow V_ {30 \ Omega} = 84V $$
Do đó, điện áp trên điện trở 30 Ω của đoạn mạch đã cho là 84 V.
Note 1- Từ ví dụ trên, chúng ta có thể kết luận rằng chúng ta phải giải phương trình lưới 'm', nếu mạch điện đang có lưới 'm'. Đó là lý do tại sao chúng ta có thể chọn phân tích Mesh khi số lượng mắt lưới nhỏ hơn số lượng nút chính (ngoại trừ nút tham chiếu) của bất kỳ mạch điện nào.
Note 2 - Chúng ta có thể chọn phân tích Nodal hoặc phân tích Mesh, khi số lượng mắt lưới bằng số nút chính (trừ nút tham chiếu) trong bất kỳ mạch điện nào.