Lý thuyết mạng - Định lý chồng chất

Superposition theoremdựa trên khái niệm tuyến tính giữa phản ứng và kích thích của một mạch điện. Nó nói rằng đáp ứng trong một nhánh cụ thể của mạch tuyến tính khi nhiều nguồn độc lập hoạt động cùng một lúc tương đương với tổng các phản hồi do mỗi nguồn độc lập tác động tại một thời điểm.

Trong phương pháp này, chúng tôi sẽ chỉ xem xét one independent sourcetại một thời điểm. Vì vậy, chúng ta phải loại bỏ các nguồn độc lập còn lại khỏi mạch. Chúng ta có thể loại bỏ các nguồn điện áp bằng cách nối tắt hai đầu nối của chúng và tương tự, các nguồn dòng điện bằng cách mở hai đầu nối của chúng.

Do đó, chúng ta cần tìm phản hồi trong một nhánh cụ thể ‘n’ timesnếu có 'n' nguồn độc lập. Đáp ứng trong một nhánh cụ thể có thể là dòng điện chạy qua nhánh đó hoặc điện áp trên nhánh đó.

Quy trình của Định lý chồng chất

Thực hiện theo các bước sau để tìm phản ứng trong một nhánh cụ thể bằng cách sử dụng định lý chồng chất.

Step 1 - Tìm phản hồi trong một nhánh cụ thể bằng cách xem xét một nguồn độc lập và loại bỏ các nguồn độc lập còn lại có trong mạng.

Step 2 - Lặp lại Bước 1 cho tất cả các nguồn độc lập có trong mạng.

Step 3 - Thêm tất cả các phản hồi để có được phản hồi tổng thể trong một nhánh cụ thể khi tất cả các nguồn độc lập đều có trong mạng.

Thí dụ

Tìm cường độ dòng điện chạy qua điện trở 20 Ω của đoạn mạch sau sử dụng superposition theorem.

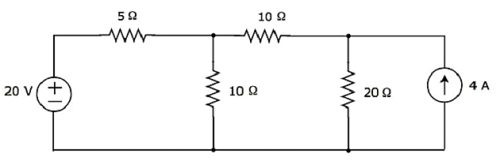
Step 1 - Ta tìm cường độ dòng điện chạy qua điện trở 20 Ω bằng cách chỉ xét 20 V voltage source. Trong trường hợp này, chúng ta có thể loại bỏ nguồn dòng 4 A bằng cách làm cho mạch hở của nó. Sơ đồ mạch sửa đổi được hiển thị trong hình sau.

Chỉ có một nút chính ngoại trừ Ground trong mạch trên. Vì vậy, chúng ta có thể sử dụngnodal analysisphương pháp. Điện áp nút V ₁ được đánh dấu trong hình sau. Ở đây, V ₁ là điện áp từ nút 1 đối với mặt đất.

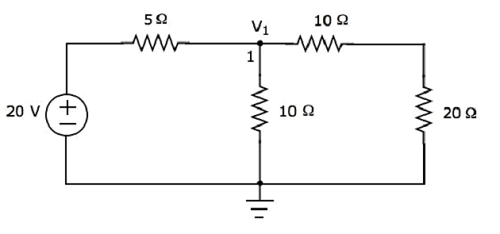
Các nodal equation tại nút 1 là

$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$

$$ \ Rightarrow \ frac {6V_1 - 120 + 3V_1 + V_1} {30} = 0 $$

$$ \ Rightarrow 10V_1 = 120 $$

$$ \ Rightarrow V_1 = 12V $$

Các current flowing through 20 Ω resistor có thể được tìm thấy bằng cách thực hiện đơn giản hóa sau đây.

$$ I_1 = \ frac {V_1} {10 + 20} $$

Thay giá trị của V ₁ vào phương trình trên.

$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0,4 A $$

Do đó, cường độ dòng điện chạy qua điện trở 20 Ω là 0.4 A, khi chỉ coi nguồn điện áp 20 V.

Step 2 - Ta tìm cường độ dòng điện chạy qua điện trở 20 Ω bằng cách chỉ xét 4 A current source. Trong trường hợp này, chúng ta có thể loại bỏ nguồn điện áp 20 V bằng cách làm ngắn mạch nó. Sơ đồ mạch sửa đổi được hiển thị trong hình sau.

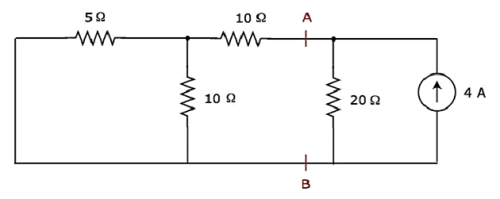
Trong đoạn mạch trên, có ba điện trở ở bên trái của các đầu nối A & B. Chúng ta có thể thay thế các điện trở này bằng một equivalent resistor. Ở đây, các điện trở 5 Ω & 10 Ω được kết nối song song và toàn bộ kết hợp mắc nối tiếp với điện trở 10 Ω.

Các equivalent resistance ở bên trái của các nhà ga A & B sẽ là

$$ R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$

Sơ đồ mạch đơn giản được hiển thị trong hình sau.

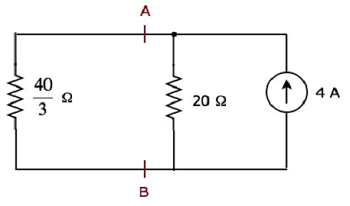
Chúng ta có thể tìm thấy dòng điện chạy qua điện trở 20 Ω, bằng cách sử dụng current division principle.

$$ I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$

Thay thế $ I_S = 4A, \: R_1 = \ frac {40} {3} \ Omega $ và $ R_2 = 20 \ Omega $ trong phương trình trên.

$$ I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1,6 A $$

Do đó, cường độ dòng điện chạy qua điện trở 20 Ω là 1.6 A, khi chỉ coi nguồn dòng 4 A.

Step 3 - Ta sẽ nhận được dòng điện chạy qua điện trở 20 Ω của đoạn mạch đã cho bằng cách thực hiện addition of two currents mà chúng ta đã đạt được ở bước 1 và bước 2. Về mặt toán học, nó có thể được viết là

$$ I = I_1 + I_2 $$

Thay vào đó, giá trị của I ₁ và I ₂ trong phương trình trên.

$$ I = 0,4 + 1,6 = 2 A $$

Do đó, cường độ dòng điện chạy qua điện trở 20 Ω của đoạn mạch đã cho là 2 A.

Note - Chúng ta không thể áp dụng trực tiếp định lý chồng chất để tìm lượng powerđược phân phối cho bất kỳ điện trở nào có trong mạch tuyến tính, chỉ bằng cách thực hiện việc cộng công suất được phân phối cho điện trở đó do mỗi nguồn độc lập. Thay vào đó, chúng ta có thể tính toán tổng dòng điện chạy qua hoặc điện áp trên điện trở đó bằng cách sử dụng định lý chồng chất và từ đó, chúng ta có thể tính toán lượng điện năng cung cấp cho điện trở đó bằng cách sử dụng $ I ^ 2 R $ hoặc $ \ frac {V ^ 2} {R} $.