Lý thuyết mạng - Đáp ứng của mạch DC
Nếu đầu ra của mạch điện cho đầu vào thay đổi theo thời gian, thì nó được gọi là time response. Phản ứng thời gian bao gồm hai phần sau.
- Phản hồi thoáng qua
- Phản hồi ở trạng thái ổn định
Trong chương này, trước tiên chúng ta hãy thảo luận về hai phản ứng này và sau đó quan sát hai phản ứng này trong một mạch RL nối tiếp, khi nó được kích thích bởi nguồn điện áp một chiều.
Phản hồi thoáng qua
Sau khi đặt một đầu vào vào mạch điện, đầu ra cần một thời gian nhất định để đạt trạng thái ổn định. Vì vậy, đầu ra sẽ ở trạng thái tạm thời cho đến khi nó chuyển sang trạng thái ổn định. Do đó, phản ứng của mạch điện trong trạng thái quá độ được gọi làtransient response.
Phản hồi nhất thời sẽ bằng 0 đối với các giá trị lớn của 't'. Lý tưởng nhất, giá trị này của 't' phải là vô cùng. Nhưng, thực tếfive time constants là đủ.
Sự hiện diện hoặc Sự vắng mặt của Người chuyển tiếp
Quá độ xảy ra trong phản hồi do sudden changetrong các nguồn được đưa vào mạch điện và / hoặc do hoạt động chuyển mạch. Có thể có hai hành động chuyển đổi. Đó là công tắc mở và công tắc đóng.
Các transient một phần sẽ not presenttrong phản ứng của mạch điện hoặc mạng, nếu nó chỉ chứa điện trở. Bởi vìresistor có khả năng điều chỉnh bất kỳ lượng điện áp và dòng điện nào.
Các transient part occurs trong phản ứng của một mạch điện hoặc mạng do sự hiện diện của các phần tử lưu trữ năng lượng như inductor and capacitor. Bởi vì chúng không thể thay đổi năng lượng được lưu trữ trong các nguyên tố đó ngay lập tức.
Hành vi cuộn cảm
Giả sử hành động chuyển đổi diễn ra tại t = 0.Inductor currentkhông thay đổi ngay lập tức, khi hành động chuyển đổi diễn ra. Điều đó có nghĩa là, giá trị của dòng điện dẫn ngay sau hành động chuyển mạch sẽ giống như giá trị ngay trước khi hành động chuyển mạch.
Về mặt toán học, nó có thể được biểu diễn dưới dạng
$$ i_L (0 ^ +) = i_L (0 ^ -) $$
Hành vi của tụ điện
Các capacitor voltagekhông thay đổi tức thời tương tự như dòng điện dẫn, khi hành động chuyển mạch diễn ra. Điều đó có nghĩa là, giá trị của điện áp tụ điện ngay sau hành động chuyển mạch sẽ giống như giá trị của ngay trước khi hành động chuyển mạch.
Về mặt toán học, nó có thể được biểu diễn dưới dạng
$$ v_c (0 ^ +) = v_c (0 ^ -) $$
Phản hồi ở trạng thái ổn định
Phần phản hồi thời gian vẫn còn ngay cả sau khi phản hồi thoáng qua đã trở thành giá trị 0 đối với các giá trị lớn của 't' được gọi là steady state response. Điều này có nghĩa là, sẽ không có bất kỳ phần nào nhất thời trong phản hồi ở trạng thái ổn định.
Hành vi cuộn cảm
Nếu nguồn độc lập được nối với mạch điện hoặc mạng điện có một hoặc nhiều cuộn cảm và điện trở (tùy chọn) trong một thời gian dài, thì mạch điện hoặc mạng điện đó được cho là ở trạng thái ổn định. Do đó, năng lượng tích trữ trong (các) cuộn cảm của mạch điện đó là cực đại và không đổi.
Về mặt toán học, nó có thể được biểu diễn dưới dạng
$ W_L = \ frac {L {i_L} ^ 2} {2} = $ Tối đa & hằng số
$ \ Rightarrow i_L = $ Tối đa & hằng số
Do đó, cuộn cảm hoạt động như một constant current source ở trạng thái ổn định.
Điện áp trên cuộn cảm sẽ là
$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$
Vì vậy, cuộn cảm hoạt động như một short circuit ở trạng thái ổn định.
Hành vi của tụ điện
Nếu nguồn độc lập được nối với mạch điện hoặc mạng điện có một hoặc nhiều tụ điện và điện trở (tùy chọn) trong thời gian dài, thì mạch điện hoặc mạng điện đó được cho là ở trạng thái ổn định. Do đó, năng lượng tích trữ trong (các) tụ điện của mạch điện đó là cực đại và không đổi.
Về mặt toán học, nó có thể được biểu diễn dưới dạng
$ W_c = \ frac {C {v_c} ^ 2} {2} = $ Cực đại & hằng số
$ \ Rightarrow v_c = $ Tối đa & hằng số
Do đó, tụ điện hoạt động như một constant voltage source ở trạng thái ổn định.
Dòng điện chạy qua tụ điện sẽ là
$$ i_c = C \ frac {dv_c} {dt} = 0A $$
Vì vậy, tụ điện hoạt động như một open circuit ở trạng thái ổn định.
Tìm phản hồi của mạch RL loạt
Hãy xem xét những điều sau series RL circuit biểu đồ.
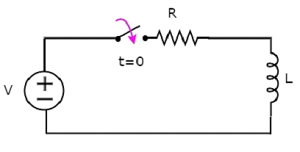
Trong mạch trên, switch đã được giữ openđến t = 0 và đóng ở t = 0. Vậy nguồn điện một chiều có V vôn không mắc vào đoạn mạch RL nối tiếp tính đến thời điểm này. Do đó, cóno initial current chảy qua cuộn cảm.
Sơ đồ mạch, khi switch trong closed vị trí được hiển thị trong hình sau.
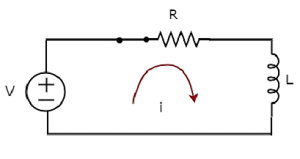
Bây giờ, hiện tại i chảy trong toàn bộ mạch, vì nguồn điện áp một chiều có V vôn được mắc vào mạch RL nối tiếp.
Bây giờ, áp dụng KVL xung quanh vòng lặp.
$$ V = Ri + L \ frac {di} {dt} $$
$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1
Phương trình trên là một phương trình vi phân bậc nhất và nó có dạng
$ \ frac {dy} {dt} + Py = Q $Equation 2
Bởi comparing Phương trình 1 và phương trình 2, chúng ta sẽ nhận được các quan hệ sau.
$$ x = t $$
$$ y = i $$
$$ P = \ frac {R} {L} $$
$$ Q = \ frac {V} {L} $$
Các solution của phương trình 2 sẽ là
$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3
Ở đâu, k là hằng số.
Thay thế các giá trị của x, y, P & Q trong Công thức 3.
$ tức là ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $
$ \ Rightarrow tức là ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $
$ \ Rightarrow tức là ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $
$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $Equation 4
Ta biết rằng không có dòng điện ban đầu trong mạch. Do đó, thay thế, t = 0 và = 0 trong phương trình 4 để tìm giá trị của hằng số k.
$$ 0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)} $$
$$ 0 = \ frac {V} {R} + k (1) $$
$$ k = - \ frac {V} {R} $$
Thay thế, giá trị của k trong phương trình 4.
$$ i = \ frac {V} {R} + \ lgroup - \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
$$ i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
Do đó, current chảy qua mạch là
$ i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5
Vậy đáp ứng của đoạn mạch RL nối tiếp khi được kích thích bằng nguồn điện áp một chiều có hai số hạng sau.
Số hạng đầu tiên $ - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ tương ứng với transient response.
Số hạng thứ hai $ \ frac {V} {R} $ tương ứng với steady state response. Hai phản ứng này được hiển thị trong hình sau.
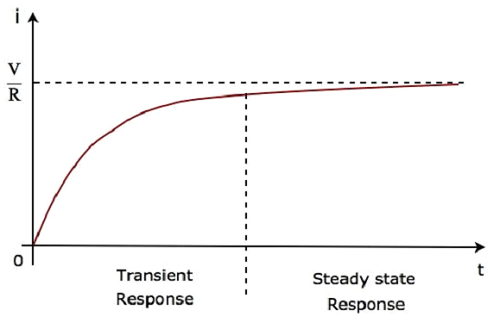
Chúng ta có thể viết lại phương trình 5 như sau:
$ i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $
$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6
Ở đâu, τ là time constant và giá trị của nó bằng $ \ frac {L} {R} $.
Cả phương trình 5 và phương trình 6 đều giống nhau. Nhưng, chúng ta có thể dễ dàng hiểu dạng sóng trên của dòng điện chạy qua mạch từ phương trình 6 bằng cách thay thế một vài giá trị củat như 0, τ, 2τ, 5τ, v.v.
Trong dạng sóng ở trên của dòng điện chạy qua mạch, phản ứng nhất thời sẽ hiển thị tối đa năm hằng số thời gian từ 0, trong khi phản ứng trạng thái ổn định sẽ xuất hiện từ năm hằng số thời gian trở đi.