Lý thuyết mạng - Hướng dẫn nhanh
Network theorylà nghiên cứu giải quyết các vấn đề của mạch điện hoặc mạng điện. Trong chương mở đầu này, trước tiên chúng ta hãy thảo luận về thuật ngữ cơ bản của mạch điện và các loại phần tử mạng.
Thuật ngữ cơ bản
Trong Lý thuyết mạng, chúng ta thường gặp các thuật ngữ sau:
- Mạch điện
- Mạng điện
- Current
- Voltage
- Power
Vì vậy, chúng ta bắt buộc phải thu thập một số kiến thức cơ bản về các thuật ngữ này trước khi tiếp tục. Hãy bắt đầu với Mạch điện.
Mạch điện
Một mạch điện chứa một đường dẫn kín để cung cấp dòng electron từ nguồn điện áp hoặc nguồn dòng điện. Các phần tử có trong mạch điện sẽ ởseries connection, parallel connection, hoặc trong bất kỳ sự kết hợp nào của kết nối nối tiếp và song song.
Mạng điện
Mạng điện không cần phải có đường dẫn kín để cung cấp dòng electron từ nguồn điện áp hoặc nguồn dòng điện. Do đó, chúng ta có thể kết luận rằng "tất cả các mạch điện đều là mạng điện" nhưng điều ngược lại không cần phải đúng.
Hiện hành
Hiện tại "I"chảy qua một vật dẫn không là gì khác ngoài tốc độ thời gian của dòng điện tích. Về mặt toán học, nó có thể được viết là
$$I = \frac{dQ}{dt}$$
Ở đâu,
Q là phí và đơn vị của nó là Coloumb.
t là thời gian và đơn vị của nó là thứ hai.
Tương tự, dòng điện có thể được coi là dòng nước chảy qua một đường ống. Dòng điện được đo bằngAmpere.
Nói chung, Electron current chảy từ đầu cuối âm của nguồn sang đầu cuối dương, ngược lại, Conventional current chảy từ cực dương của nguồn sang cực âm.
Electron current thu được do chuyển động của các electron tự do, trong khi, Conventional currentcó được do sự chuyển động của các điện tích dương tự do. Cả hai điều này được gọi làelectric current.
Vôn
Điện áp "V"không là gì khác ngoài sức điện động gây ra dòng điện (electron). Về mặt toán học, nó có thể được viết là
$$V = \frac{dW}{dQ}$$
Ở đâu,
W là thế năng và đơn vị của nó là Joule.
Q là phí và đơn vị của nó là Coloumb.
Tương tự, Điện áp có thể được coi là áp lực của nước khiến nước chảy qua đường ống. Nó được đo lường về mặtVolt.
Quyền lực
Sức mạnh "P"không là gì khác ngoài tốc độ thời gian của dòng năng lượng điện. Về mặt toán học, nó có thể được viết là
$$P = \frac{dW}{dt}$$
Ở đâu,
W là năng lượng điện và nó được đo bằng Joule.
t là thời gian và nó được đo bằng giây.
Ta có thể viết lại phương trình trên a
$$P = \frac{dW}{dt} = \frac{dW}{dQ} \times \frac{dQ}{dt} = VI$$
Vì thế, power không là gì ngoài product điện áp V và hiện tại I. Đơn vị của nó làWatt.
Các loại phần tử mạng
Chúng ta có thể phân loại các phần tử Mạng thành nhiều loại khác nhau dựa trên một số tham số. Sau đây là các loại phần tử Mạng:
Yếu tố hoạt động và yếu tố bị động
Phần tử tuyến tính và phần tử phi tuyến tính
Các yếu tố song phương và các yếu tố đơn phương
Yếu tố hoạt động và yếu tố bị động
Chúng ta có thể phân loại các phần tử Mạng thành active hoặc là passive dựa trên khả năng phân phối điện.
Active Elementscung cấp năng lượng cho các phần tử khác có trong mạch điện. Đôi khi, chúng có thể hấp thụ sức mạnh như các phần tử thụ động. Điều đó có nghĩa là các phần tử tích cực có khả năng vừa phân phối vừa hấp thụ năng lượng.Examples: Nguồn điện áp và nguồn dòng điện.
Passive Elementskhông thể cung cấp năng lượng (năng lượng) cho các phần tử khác, tuy nhiên chúng có thể hấp thụ năng lượng. Điều đó có nghĩa là các phần tử này tiêu tán năng lượng dưới dạng nhiệt hoặc tích trữ năng lượng dưới dạng từ trường hoặc điện trường.Examples: Điện trở, cuộn cảm và tụ điện.
Phần tử tuyến tính và phần tử phi tuyến tính
Chúng ta có thể phân loại các phần tử mạng là linear hoặc là non-linear dựa vào đặc tính của chúng để tuân theo tính chất của tuyến tính.
Linear Elements là các phần tử thể hiện mối quan hệ tuyến tính giữa điện áp và dòng điện. Examples: Điện trở, cuộn cảm và tụ điện.
Non-Linear Elements là những thứ không thể hiện mối quan hệ tuyến tính giữa điện áp và dòng điện. Examples: Nguồn điện áp và nguồn dòng điện.
Các yếu tố song phương và các yếu tố đơn phương
Các phần tử mạng cũng có thể được phân loại là bilateral hoặc là unilateral dựa trên hướng của dòng điện chạy qua các phần tử mạng.
Bilateral Elements là các phần tử cho phép dòng điện theo cả hai hướng và có cùng trở kháng theo một trong hai hướng của dòng điện. Examples: Điện trở, cuộn cảm và tụ điện.
Khái niệm về các yếu tố Song phương được minh họa trong các hình sau.
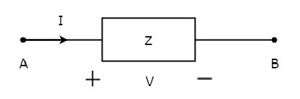
Trong hình trên, dòng điện (I) chạy từ đầu A đến B qua một phần tử thụ động có trở kháng Z Ω. Nó là tỷ số của điện áp (V) trên phần tử đó giữa các đầu nối A & B và dòng điện (I).
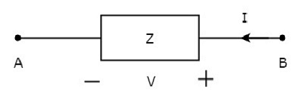
Trong hình trên, dòng điện (I) chạy từ đầu B đến A qua một phần tử thụ động có trở kháng Z Ω. Điều đó có nghĩa là dòng điện (–I) đang chạy từ các cực A đến B. Trong trường hợp này, chúng ta cũng sẽ nhận được cùng một giá trị trở kháng, vì cả dòng điện và điện áp đều có dấu âm đối với các cực A & B.
Unilateral Elementslà những dòng cho phép dòng điện chỉ theo một chiều. Do đó, chúng cung cấp các trở kháng khác nhau theo cả hai hướng.
Chúng ta đã thảo luận về các loại phần tử mạng trong chương trước. Bây giờ, hãy để chúng tôi xác địnhnature of network elements từ các đặc điểm VI cho trong các ví dụ sau.
ví dụ 1
Các V-I characteristics của một phần tử mạng được hiển thị bên dưới.
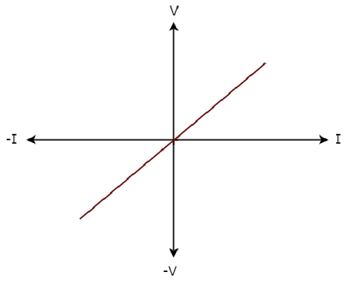
Step 1 - Xác minh phần tử mạng là linear hoặc là non-linear.
Từ hình trên, đặc điểm VI của phần tử mạng là một đường thẳng đi qua gốc tọa độ. Do đó, nó là mộtLinear element.
Step 2 - Xác minh phần tử mạng là active hoặc là passive.
Các đặc điểm VI đã cho của một phần tử mạng nằm ở góc phần tư thứ nhất và thứ ba.
bên trong first quadrant, giá trị của cả điện áp (V) và cường độ dòng điện (I) đều dương. Vì vậy, tỷ số điện áp (V) và dòng điện (I) cho giá trị trở kháng dương.
Tương tự, trong third quadrant, giá trị của cả điện áp (V) và cường độ dòng điện (I) đều có giá trị âm. Vì vậy, tỷ lệ điện áp (V) và dòng điện (I) tạo ra giá trị trở kháng dương.
Vì các đặc tính VI đã cho cung cấp các giá trị trở kháng dương, phần tử mạng là Passive element.
Step 3 - Xác minh phần tử mạng là bilateral hoặc là unilateral.
Với mỗi điểm (I, V) trên các đặc điểm thì tồn tại một điểm tương ứng (-I, -V) trên các đặc điểm đã cho. Do đó, phần tử mạng làBilateral element.
Do đó, các đặc điểm VI đã cho cho thấy phần tử mạng là Linear, Passivevà Bilateral element.
Ví dụ 2
Các V-I characteristics của một phần tử mạng được hiển thị bên dưới.
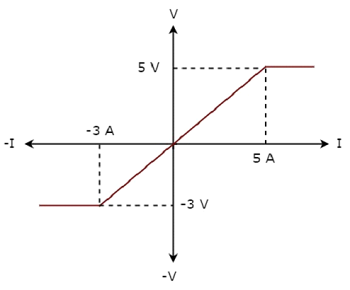
Step 1 - Xác minh phần tử mạng là linear hoặc là non-linear.
Từ hình trên cho thấy đặc điểm VI của phần tử mạng là đường thẳng chỉ nằm giữa các điểm (-3A, -3V) và (5A, 5V). Ngoài những điểm này, đặc điểm VI không tuân theo quan hệ tuyến tính. Do đó, nó là mộtNon-linear element.
Step 2 - Xác minh phần tử mạng là active hoặc là passive.
Các đặc điểm VI đã cho của một phần tử mạng nằm ở góc phần tư thứ nhất và thứ ba. Trong hai góc phần tư này, tỷ số điện áp (V) và dòng điện (I) tạo ra giá trị trở kháng dương. Do đó, phần tử mạng làPassive element.
Step 3 - Xác minh phần tử mạng là bilateral or unilateral.
Xem xét điểm (5A, 5V) trên các đặc điểm. Điểm tương ứng (-5A, -3V) tồn tại trên các đặc điểm đã cho thay vì (-5A, -5V). Do đó, phần tử mạng làUnilateral element.
Do đó, các đặc điểm VI đã cho cho thấy phần tử mạng là Non-linear, Passivevà Unilateral element.
Active Elementslà các phần tử mạng cung cấp năng lượng cho các phần tử khác có trong mạch điện. Vì vậy, các phần tử tích cực còn được gọi là nguồn điện áp hoặc loại dòng điện. Chúng tôi có thể phân loại các nguồn này thành hai loại sau:
- Nguồn độc lập
- Nguồn phụ thuộc
Nguồn độc lập
Như tên cho thấy, các nguồn độc lập tạo ra các giá trị điện áp hoặc dòng điện cố định và những giá trị này không phụ thuộc vào bất kỳ thông số nào khác. Các nguồn độc lập có thể được chia thành hai loại sau:
- Nguồn điện áp độc lập
- Nguồn hiện tại độc lập
Nguồn điện áp độc lập
Nguồn điện áp độc lập tạo ra hiệu điện thế không đổi trên hai đầu của nó. Điện áp này không phụ thuộc vào cường độ dòng điện chạy qua hai đầu của nguồn điện áp.
Độc lập ideal voltage source và đặc điểm VI của nó được thể hiện trong hình sau.
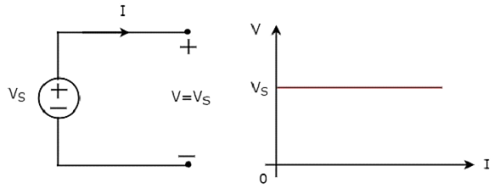
Các V-I characteristicscủa nguồn điện áp lý tưởng độc lập là một dòng không đổi, luôn bằng điện áp nguồn (VS) không phụ thuộc vào giá trị dòng điện (I). Vì vậy, điện trở bên trong của nguồn điện áp lý tưởng độc lập bằng không Ohms.
Do đó, các nguồn điện áp lý tưởng độc lập do not exist practically, bởi vì sẽ có một số lực cản bên trong.
Độc lập practical voltage source và đặc điểm VI của nó được thể hiện trong hình sau.
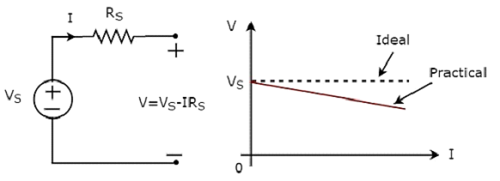
Có sự sai lệch trong các đặc tính VI của nguồn điện áp thực tế độc lập với các đặc tính VI của nguồn điện áp lý tưởng độc lập. Điều này là do điện áp giảm trên điện trở trong (R S ) của nguồn điện áp thực tế độc lập.
Nguồn hiện tại độc lập
Nguồn dòng điện độc lập tạo ra dòng điện không đổi. Dòng điện này không phụ thuộc vào điện áp trên hai đầu của nó. Độc lậpideal current source và đặc điểm VI của nó được thể hiện trong hình sau.

Các V-I characteristicscủa nguồn dòng điện lý tưởng độc lập là một dòng không đổi, dòng điện này luôn bằng dòng điện nguồn (I S ) không phụ thuộc vào giá trị hiệu điện thế (V). Vì vậy, điện trở bên trong của nguồn dòng điện lý tưởng độc lập là vô hạn ohms.
Do đó, các nguồn dòng điện lý tưởng độc lập do not exist practically, bởi vì sẽ có một số lực cản bên trong.
Độc lập practical current source và đặc điểm VI của nó được thể hiện trong hình sau.
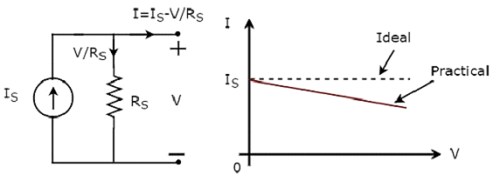
Có sự sai lệch trong các đặc tính VI của nguồn dòng điện thực tế độc lập so với các đặc tính VI của nguồn dòng điện lý tưởng độc lập. Điều này là do lượng dòng điện chạy qua điện trở shunt bên trong (R S ) của nguồn dòng điện thực tế độc lập.
Nguồn phụ thuộc
Như tên cho thấy, các nguồn phụ thuộc tạo ra lượng điện áp hoặc dòng điện phụ thuộc vào một số điện áp hoặc dòng điện khác. Nguồn phụ thuộc còn được gọi làcontrolled sources. Nguồn phụ thuộc có thể được chia thành hai loại sau:
- Nguồn điện áp phụ thuộc
- Nguồn hiện tại phụ thuộc
Nguồn điện áp phụ thuộc
Nguồn điện áp phụ thuộc tạo ra hiệu điện thế trên hai đầu của nó. Lượng điện áp này phụ thuộc vào một số điện áp hoặc dòng điện khác. Do đó, các nguồn điện áp phụ thuộc có thể được phân loại thêm thành hai loại sau:
- Nguồn điện áp phụ thuộc (VDVS)
- Nguồn điện áp phụ thuộc hiện tại (CDVS)
Các nguồn điện áp phụ thuộc được biểu diễn bằng các dấu '+' và '-' bên trong hình thoi. Độ lớn của nguồn điện áp có thể được biểu diễn bên ngoài hình thoi.
Nguồn hiện tại phụ thuộc
Nguồn dòng phụ thuộc tạo ra dòng điện. Lượng dòng điện này phụ thuộc vào một số điện áp hoặc dòng điện khác. Do đó, các nguồn dòng phụ thuộc có thể được phân loại thêm thành hai loại sau:
- Nguồn hiện tại phụ thuộc điện áp (VDCS)
- Nguồn hiện tại phụ thuộc hiện tại (CDCS)
Nguồn dòng phụ thuộc được biểu diễn bằng một mũi tên bên trong hình thoi. Độ lớn của nguồn dòng điện có thể được biểu diễn bên ngoài hình thoi.
Chúng ta có thể quan sát các nguồn phụ thuộc hoặc được kiểm soát này trong các mô hình tương đương của bóng bán dẫn.
Kỹ thuật chuyển đổi nguồn
Chúng tôi biết rằng có hai nguồn thực tế, đó là voltage source và current source. Chúng tôi có thể chuyển đổi (chuyển đổi) nguồn này thành nguồn kia dựa trên yêu cầu, đồng thời giải quyết các vấn đề mạng.
Kỹ thuật chuyển đổi nguồn này thành nguồn khác được gọi là source transformation technique. Sau đây là hai phép biến đổi nguồn có thể có:
- Nguồn điện áp thực tế thành nguồn dòng điện thực tế
- Nguồn dòng điện thực tế thành nguồn điện áp thực tế
Nguồn điện áp thực tế thành nguồn dòng điện thực tế
Sự biến đổi của nguồn điện áp thực tế thành nguồn dòng điện thực tế được biểu diễn trong hình sau
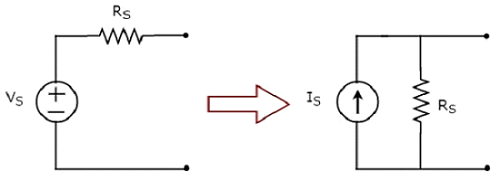
Practical voltage sourcegồm nguồn điện áp (V S ) mắc nối tiếp với một điện trở (R S ). Điều này có thể được chuyển đổi thành một nguồn hiện tại thực tế như thể hiện trong hình. Nó bao gồm một nguồn hiện tại (I S ) song song với một điện trở (R S ).
Giá trị của IS sẽ bằng tỷ lệ của V S và R S . Về mặt toán học, nó có thể được biểu diễn dưới dạng
$$I_S = \frac{V_S}{R_S}$$
Nguồn dòng điện thực tế thành nguồn điện áp thực tế
Sự biến đổi của nguồn dòng điện thực tế thành nguồn điện áp thực tế được biểu diễn trong hình sau.
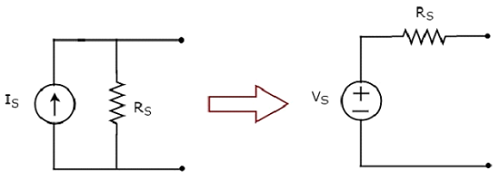
Nguồn dòng thực tế gồm nguồn dòng (I S ) mắc song song với một điện trở (R S ). Điều này có thể được chuyển đổi thành một nguồn điện áp thực tế như trong hình. Nó gồm một nguồn điện áp (V S ) mắc nối tiếp với một điện trở (R S ).
Giá trị của V S sẽ tương đương với sản phẩm của I S và R S . Về mặt toán học, nó có thể được biểu diễn dưới dạng
$$V_S = I_S R_S$$
Trong chương này, chúng ta sẽ thảo luận chi tiết về các phần tử thụ động như Điện trở, Cuộn cảm và Tụ điện. Chúng ta hãy bắt đầu với Điện trở.
Điện trở
Chức năng chính của Điện trở là chống lại hoặc hạn chế dòng điện. Do đó, các điện trở được sử dụng để hạn chế lượng dòng điện và / hoặc phân chia (chia sẻ) điện áp.
Cho cường độ dòng điện chạy qua điện trở là I ampe và hiệu điện thế trên nó là V vôn. Cácsymbol của điện trở cùng với dòng điện, I và hiệu điện thế, V được thể hiện trong hình sau.
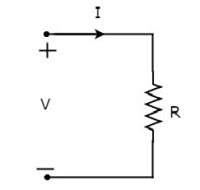
Dựa theo Ohm’s law, hiệu điện thế trên điện trở là tích của dòng điện chạy qua nó và điện trở của điện trở đó. Mathematically, nó có thể được biểu thị là
$V = IR$ Equation 1
$\Rightarrow I = \frac{V}{R}$Equation 2
Ở đâu, R là điện trở của một điện trở.
Từ phương trình 2, chúng ta có thể kết luận rằng dòng điện chạy qua điện trở tỷ lệ thuận với điện áp đặt trên điện trở và tỷ lệ nghịch với điện trở của điện trở.
Power trong một phần tử mạch điện có thể được biểu diễn dưới dạng
$P = VI$Equation 3
Thay thế, Phương trình 1 trong Phương trình 3.
$P = (IR)I$
$\Rightarrow P = I^2 R$ Equation 4
Thay thế, Phương trình 2 trong Phương trình 3.
$P = V \lgroup \frac{V}{R} \rgroup$
$\Rightarrow P = \frac{V^2}{R}$ Equation 5
Vì vậy, chúng ta có thể tính toán lượng điện năng tiêu tán trong điện trở bằng cách sử dụng một trong các công thức được đề cập trong phương trình 3 đến 5.
Cuộn cảm
Nói chung, cuộn cảm sẽ có số vòng dây. Do đó, chúng tạo ra từ thông khi dòng điện chạy qua nó. Vì vậy, tổng lượng từ thông tạo ra bởi một cuộn cảm phụ thuộc vào dòng điện chạy qua nó và chúng có mối quan hệ tuyến tính.
Mathematically, nó có thể được viết là
$$\Psi \: \alpha \: I$$
$$\Rightarrow \Psi = LI$$
Ở đâu,
Ψ là tổng từ thông
L là độ tự cảm của một cuộn cảm
Cho cường độ dòng điện chạy qua cuộn cảm là I ampe và hiệu điện thế qua cuộn cảm là V vôn. Cácsymbolcủa cuộn cảm cùng với dòng điện I và hiệu điện thế V được biểu diễn trong hình sau.
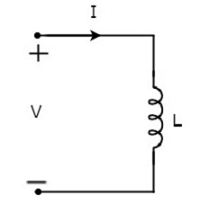
Dựa theo Faraday’s law, điện áp trên cuộn cảm có thể được viết là
$$V = \frac{d\Psi}{dt}$$
Thay Ψ = LI vào phương trình trên.
$$V = \frac{d(LI)}{dt}$$
$$\Rightarrow V = L \frac{dI}{dt}$$
$$\Rightarrow I = \frac{1}{L} \int V dt$$
Từ các phương trình trên, chúng ta có thể kết luận rằng tồn tại một linear relationship giữa điện áp trên cuộn cảm và dòng điện chạy qua nó.
Chúng ta biết rằng power trong một phần tử mạch điện có thể được biểu diễn dưới dạng
$$P = VI$$
Người thay thế $V = L \frac{dI}{dt}$ trong phương trình trên.
$$P = \lgroup L \frac{dI}{dt}\rgroup I$$
$$\Rightarrow P = LI \frac{dI}{dt}$$
Bằng cách tích phân phương trình trên, chúng ta sẽ nhận được energy được lưu trữ trong một cuộn cảm như
$$W = \frac{1}{2} LI^2$$
Vì vậy, cuộn cảm lưu trữ năng lượng dưới dạng từ trường.
Tụ điện
Nói chung, tụ điện có hai bản dẫn điện, ngăn cách nhau bằng môi trường điện môi. Nếu điện áp dương được đặt trên tụ điện, thì nó lưu trữ điện tích dương. Tương tự, nếu điện áp âm được đặt trên tụ điện, thì nó sẽ tích trữ điện tích âm.
Vì vậy, lượng điện tích lưu trữ trong tụ điện phụ thuộc vào điện áp đặt vào Vxuyên qua nó và chúng có mối quan hệ tuyến tính. Về mặt toán học, nó có thể được viết là
$$Q \: \alpha \: V$$
$$\Rightarrow Q = CV$$
Ở đâu,
Q là điện tích được lưu trữ trong tụ điện.
C là điện dung của tụ điện.
Cho cường độ dòng điện chạy qua tụ điện là I ampe và hiệu điện thế qua tụ là V vôn. Kí hiệu của tụ điện cùng với dòng điện I và hiệu điện thế V được thể hiện trong hình sau.
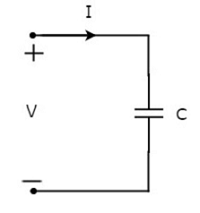
Chúng tôi biết rằng current không là gì ngoài time rate of flow of charge. Về mặt toán học, nó có thể được biểu diễn dưới dạng
$$I = \frac{dQ}{dt}$$
Người thay thế $Q = CV$ trong phương trình trên.
$$I = \frac{d(CV)}{dt}$$
$$\Rightarrow I = C \frac{dV}{dt}$$
$$\Rightarrow V = \frac{1}{C} \int I dt$$
Từ các phương trình trên, chúng ta có thể kết luận rằng tồn tại một linear relationship giữa hiệu điện thế trên tụ điện và cường độ dòng điện chạy qua nó.
Chúng ta biết rằng power trong một phần tử mạch điện có thể được biểu diễn dưới dạng
$$P = VI$$
Người thay thế $I = C \frac{dV}{dt}$ trong phương trình trên.
$$P = V \lgroup C \frac{dV}{dt} \rgroup$$
$$\Rightarrow P = CV \frac{dV}{dt}$$
Bằng cách tích phân phương trình trên, chúng ta sẽ nhận được energy được lưu trữ trong tụ điện như
$$W = \frac{1}{2}CV^2$$
Vì vậy, tụ điện lưu trữ năng lượng dưới dạng điện trường.
Các phần tử mạng có thể là một trong số active hoặc là passivekiểu. Bất kỳ mạch điện hoặc mạng nào đều chứa một trong hai loại phần tử mạng này hoặc kết hợp cả hai.
Bây giờ, chúng ta hãy thảo luận về hai luật sau, được biết đến nhiều như Kirchhoff’s laws.
- Luật hiện hành của Kirchhoff
- Định luật điện áp Kirchhoff
Luật hiện hành của Kirchhoff
Định luật hiện tại của Kirchhoff (KCL) nói rằng tổng đại số của dòng điện đi (hoặc đi vào) một nút bằng không.
A Nodelà một điểm mà hai hoặc nhiều phần tử mạch được kết nối với nó. Nếu chỉ có hai phần tử mạch được kết nối với một nút, thì nó được cho là nút đơn giản. Nếu ba hoặc nhiều phần tử mạch được kết nối với một nút, thì nó được cho làPrincipal Node.
Mathematically, KCL có thể được đại diện là
$$\displaystyle\sum\limits_{m=1}^M I_m = 0$$
Ở đâu,
Imlà dòng nhánh thứ m rời khỏi nút.
M là số nhánh được kết nối với một nút.
Tuyên bố trên của KCLcũng có thể được biểu thị bằng "tổng đại số của dòng điện đi vào một nút bằng tổng đại số của dòng điện ra khỏi một nút". Hãy để chúng tôi kiểm chứng nhận định này qua ví dụ sau.
Thí dụ
Viết KCL equation tại nút P của hình sau.
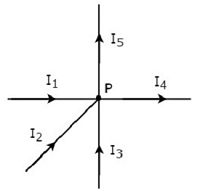
Trong hình trên, các dòng nhánh I 1 , I 2 và I 3 làentering tại nút P. Vì vậy, hãy xem xét các dấu hiệu tiêu cực cho ba dòng điện này.
Trong hình trên, các dòng nhánh I 4 và I 5 làleaving từ nút P. Vì vậy, hãy xem xét các dấu hiệu tích cực cho hai dòng điện này.
Các KCL equation tại nút P sẽ là
$$- I_1 - I_2 - I_3 + I_4 + I_5 = 0$$
$$\Rightarrow I_1 + I_2 + I_3 = I_4 + I_5$$
Trong phương trình trên, bên trái biểu thị tổng dòng điện đi vào, trong khi bên tay phải biểu thị tổng dòng điện đi ra.
Trong hướng dẫn này, chúng ta sẽ xem xét dấu tích cực khi dòng điện rời khỏi một nút và dấu âm khi nó đi vào một nút. Tương tự, bạn có thể xem xét dấu âm khi dòng điện rời khỏi một nút và dấu tích cực khi nó đi vào một nút. Trong cả hai trường hợp,result will be same.
Note - KCL độc lập với bản chất của các phần tử mạng được kết nối với một nút.
Định luật điện áp Kirchhoff
Định luật Điện áp của Kirchhoff (KVL) phát biểu rằng tổng đại số của điện áp xung quanh một vòng lặp hoặc lưới bằng không.
A Looplà một đường dẫn kết thúc tại cùng một nút nơi nó bắt đầu. Ngược lại, mộtMesh là một vòng lặp không chứa bất kỳ vòng lặp nào khác bên trong nó.
Về mặt toán học, KVL có thể được biểu diễn dưới dạng
$$\displaystyle\sum\limits_{n=1}^N V_n = 0$$
Ở đâu,
Vnlà điện áp của phần tử thứ n trong một vòng lặp (lưới).
N là số phần tử mạng trong vòng lặp (lưới).
Tuyên bố trên của KVLcũng có thể được biểu thị bằng "tổng đại số của nguồn điện áp bằng tổng đại số của điện áp rơi trong một vòng lặp." Hãy để chúng tôi xác minh tuyên bố này với sự trợ giúp của ví dụ sau.
Thí dụ
Viết KVL equation xung quanh vòng lặp của đoạn mạch sau.
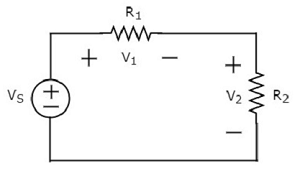
Sơ đồ mạch điện trên gồm nguồn điện có hiệu điện thế V S mắc nối tiếp với hai điện trở R 1 và R 2 . Điện áp rơi trên điện trở R 1 và R 2 là V 1 và V 2 tương ứng.
Ứng dụng KVL xung quanh vòng lặp.
$$V_S - V_1 - V_2 = 0$$
$$\Rightarrow V_S = V_1 + V_2$$
Trong phương trình trên, số hạng bên trái biểu thị nguồn điện áp đơn VS. Trong khi đó, phía bên phải đại diện chosum of voltage drops. Trong ví dụ này, chúng tôi chỉ xem xét một nguồn điện áp. Đó là lý do tại sao phía bên trái chỉ chứa một số hạng. Nếu chúng ta xem xét nhiều nguồn điện áp, thì phía bên trái chứa tổng các nguồn điện áp.
Trong hướng dẫn này, chúng tôi coi dấu hiệu của điện áp của mỗi phần tử là cực của thiết bị đầu cuối thứ hai hiện diện khi di chuyển quanh vòng lặp. Tương tự như vậy, bạn có thể coi dấu hiệu của mỗi điện áp là cực của cực đầu tiên hiện diện trong khi di chuyển quanh vòng lặp. Trong cả hai trường hợp,result will be same.
Note - KVL không phụ thuộc vào bản chất của các phần tử mạng có trong một vòng lặp.
Trong chương này, chúng ta hãy thảo luận về hai nguyên tắc phân chia sau đây của các đại lượng điện.
- Nguyên tắc phân chia hiện tại
- Nguyên tắc phân chia điện áp
Nguyên tắc phân chia hiện tại
Khi hai hoặc nhiều phần tử thụ động được kết nối song song, lượng dòng điện chạy qua mỗi phần tử sẽ divided (được chia sẻ) với nhau từ dòng điện đang đi vào nút.
Hãy xem xét những điều sau circuit diagram.
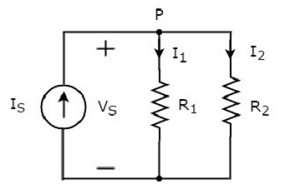
Sơ đồ mạch trên gồm một nguồn dòng vào IS mắc song song hai điện trở R1 và R2. Điện áp trên mỗi phần tử làVS. Dòng điện chạy qua các điện trởR1 và R2 Chúng tôi I1 và I2 tương ứng.
Các KCL equation tại nút P sẽ là
$$I_S = I_1 + I_2$$
Người thay thế $I_1 = \frac{V_S}{R_1}$ và $I_2 = \frac{V_S}{R_2}$ trong phương trình trên.
$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} = V_S \lgroup \frac {R_2 + R_1 }{R_1 R_2} \rgroup$$
$$\Rightarrow V_S = I_S \lgroup \frac{R_1R_2}{R_1 + R_2} \rgroup$$
Thay giá trị của V S bằng$I_1 = \frac{V_S}{R_1}$.
$$I_1 = \frac{I_S}{R_1}\lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$
$$\Rightarrow I_1 = I_S\lgroup \frac{R_2}{R_1 + R_2} \rgroup$$
Thay giá trị của V S bằng$I_2 = \frac{V_S}{R_2}$.
$$I_2 = \frac{I_S}{R_2} \lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$
$$\Rightarrow I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$
Từ phương trình I 1 và I 2 , chúng ta có thể tổng quát rằng dòng điện chạy qua bất kỳ phần tử thụ động nào có thể được tìm thấy bằng cách sử dụng công thức sau.
$$I_N = I_S \lgroup \frac{Z_1\rVert Z_2 \rVert...\rVert Z_{N-1}}{Z_1 + Z_2 + ... + Z_N}\rgroup$$
Điều này được gọi là current division principle và nó có thể áp dụng, khi hai hoặc nhiều phần tử thụ động được kết nối song song và chỉ có một dòng điện đi vào nút.
Ở đâu,
I N là dòng điện chạy qua phần tử thụ động của nhánh thứ N.
I S là dòng điện đầu vào đi vào nút.
Z 1 , Z 2 ,…, Z N lần lượt là trở kháng của nhánh thứ 1 , nhánh thứ 2 ,…, nhánh thứ N.
Nguyên tắc phân chia điện áp
Khi hai hoặc nhiều phần tử thụ động mắc nối tiếp, lượng điện áp hiện tại trên mỗi phần tử sẽ divided (được chia sẻ) giữa chúng với nhau từ điện áp có sẵn trên toàn bộ sự kết hợp đó.
Hãy xem xét những điều sau circuit diagram.
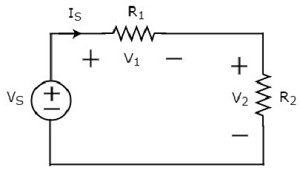
Sơ đồ mạch điện trên gồm nguồn điện có hiệu điện thế V S mắc nối tiếp với hai điện trở R 1 và R 2 . Dòng điện chảy qua các yếu tố này là tôi S . Điện áp rơi trên điện trở R 1 và R 2 là V 1 và V 2 tương ứng.
Các KVL equation xung quanh vòng lặp sẽ là
$$V_S = V_1 + V_2$$
Thay V 1 = I S R 1 và V 2 = I S R 2 vào phương trình trên
$$V_S = I_S R_1 + I_S R_2 = I_S(R_1 + R_2)$$
$$I_S = \frac{V_S}{R_1 + R_2}$$
Thay giá trị của I S vào V 1 = I S R 1 .
$$V_1 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_1$$
$$\Rightarrow V_1 = V_S \lgroup \frac {R_1}{R_1 + R_2} \rgroup$$
Thay giá trị của I S vào V 2 = I S R 2 .
$$V_2 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_2$$
$$\Rightarrow V_2 = V_S \lgroup \frac {R_2}{R_1 + R_2} \rgroup$$
Từ phương trình của V 1 và V 2 , chúng ta có thể tổng quát rằng điện áp trên bất kỳ phần tử thụ động nào có thể được tìm thấy bằng cách sử dụng công thức sau.
$$V_N = V_S \lgroup \frac {Z_N}{Z_1 + Z_2 +....+ Z_N}\rgroup$$
Điều này được gọi là voltage division principle và nó có thể áp dụng được, khi hai hoặc nhiều phần tử thụ động được mắc nối tiếp và chỉ có một điện áp khả dụng trên toàn bộ tổ hợp.
Ở đâu,
V N là điện áp trên N thứ yếu tố thụ động.
V S là điện áp đầu vào, hiện diện trên toàn bộ tổ hợp các phần tử thụ động nối tiếp.
Z 1 , Z 2 ,…, Z 3 lần lượt là trở kháng của phần tử bị động thứ 1 , phần tử bị động thứ 2 ,…, phần tử bị động thứ N.
Có hai phương pháp cơ bản được sử dụng để giải quyết bất kỳ mạng điện nào: Nodal analysis và Mesh analysis. Trong chương này, chúng ta hãy thảo luận vềNodal analysis phương pháp.
Trong phân tích Nodal, chúng ta sẽ xem xét các điện áp của nút đối với Ground. Do đó, phân tích Nodal còn được gọi làNode-voltage method.
Quy trình Phân tích Nodal
Làm theo các bước sau khi giải quyết bất kỳ mạng hoặc mạch điện nào bằng phân tích Nodal.
Step 1 - Xác định principal nodes và chọn một trong số họ là reference node. Chúng tôi sẽ coi nút tham chiếu đó là Mặt đất.
Step 2 - Gắn nhãn node voltages đối với Ground từ tất cả các nút chính ngoại trừ nút tham chiếu.
Step 3 - Viết nodal equationstại tất cả các nút chính ngoại trừ nút tham chiếu. Phương trình Nodal thu được bằng cách áp dụng KCL trước và sau đó là định luật Ohm.
Step 4 - Giải các phương trình nút thu được ở Bước 3 để có được điện áp nút.
Bây giờ, chúng ta có thể tìm thấy dòng điện chạy qua bất kỳ phần tử nào và điện áp trên bất kỳ phần tử nào có trong mạng nhất định bằng cách sử dụng điện áp nút.
Thí dụ
Tìm cường độ dòng điện chạy qua điện trở 20 Ω của đoạn mạch sau sử dụng Nodal analysis.
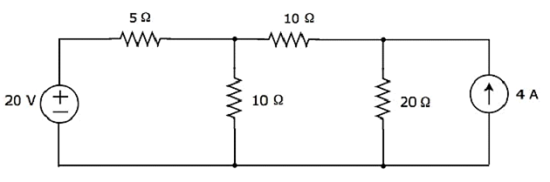
Step 1 - Có three principle nodestrong đoạn mạch trên. Chúng được gắn nhãn là 1, 2 và 3 trong hình sau.
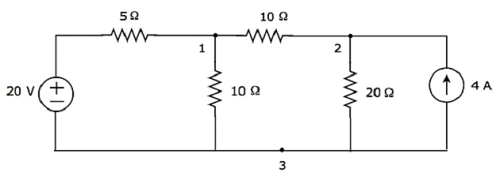
Trong hình trên, hãy xem xét node 3 làm nút tham chiếu (Ground).
Step 2- Các điện áp của nút, V 1 và V 2 , được ghi nhãn trong hình sau.
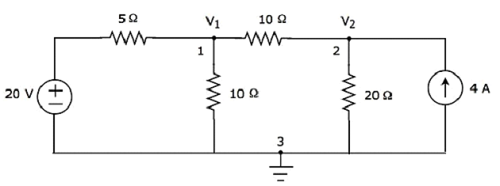
Trong hình trên, V 1 là điện áp từ nút 1 đối với đất và V 2 là điện áp từ nút 2 đối với đất.
Step 3 - Trong trường hợp này, chúng tôi sẽ nhận được two nodal equations, vì có hai nút chính, 1 và 2, khác với Ground. Khi chúng ta viết phương trình nút tại một nút, giả sử tất cả các dòng điện đang rời khỏi nút mà hướng của dòng điện không được đề cập và điện áp của nút đó lớn hơn điện áp của nút khác trong mạch.
Các nodal equation tại nút 1 là
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1 - V_2}{10} = 0$$
$$\Rightarrow \frac{2 V_1 - 40 + V_1 + V_1 - V_2}{10} = 0$$
$$\Rightarrow 4V_1 - 40 - V_2 = 0$$
$\Rightarrow V_2 = 4V_1 - 40$ Equation 1
Các nodal equation ở nút 2 là
$$-4 + \frac{V_2}{20} + \frac{V_2 - V_1}{10} = 0$$
$$\Rightarrow \frac{-80 + V_2 + 2V_2 - 2V_2}{20} = 0$$
$\Rightarrow 3V_2 − 2V_1 = 80$ Equation 2
Step 4- Tìm hiệu điện thế nút, V 1 và V 2 bằng cách giải phương trình 1 và phương trình 2.
Thay thế phương trình 1 bằng phương trình 2.
$$3(4 V_1 - 40) - 2 V_1 = 80$$
$$\Rightarrow 12 V_1 - 120 - 2V_1 =80$$
$$\Rightarrow 10 V_1 = 200$$
$$\Rightarrow V_1 = 20V$$
Thay V 1 = 20 V trong Công thức 1.
$$V_2 = 4(20) - 40$$
$$\Rightarrow V_2 = 40V$$
Vì vậy, chúng tôi nhận được điện áp nút V 1 và V 2 là20 V và 40 V tương ứng.
Step 5- Điện áp trên điện trở 20 Ω không là gì khác ngoài điện áp nút V 2 và nó bằng 40 V. Bây giờ, chúng ta có thể tìm dòng điện chạy qua điện trở 20 Ω bằng cách sử dụng định luật Ôm.
$$I_{20 \Omega} = \frac{V_2}{R}$$
Thay các giá trị của V 2 và R vào phương trình trên.
$$I_{20 \Omega} = \frac{40}{20}$$
$$\Rightarrow I_{20 \Omega} = 2A$$
Do đó cường độ dòng điện chạy qua điện trở 20 Ω của đoạn mạch đã cho là 2 A.
Note- Từ ví dụ trên, chúng ta có thể kết luận rằng chúng ta phải giải 'n' phương trình nút, nếu mạch điện có 'n' nút chính (trừ nút tham chiếu). Do đó, chúng ta có thể chọn phân tích Nodal khinumber of principal nodes (ngoại trừ nút tham chiếu) ít hơn số lượng mắt lưới của bất kỳ mạch điện nào.
Trong phân tích Mesh, chúng ta sẽ xem xét các dòng điện chạy qua mỗi mắt lưới. Do đó, phân tích lưới còn được gọi làMesh-current method.
A branchlà một đường dẫn nối hai nút và nó chứa một phần tử mạch. Nếu một nhánh chỉ thuộc về một mắt lưới, thì dòng điện nhánh sẽ bằng dòng điện lưới.
Nếu một nhánh là chung cho hai mắt lưới, thì dòng điện nhánh sẽ bằng tổng (hoặc hiệu số) của hai dòng lưới, khi chúng cùng hướng (hoặc ngược chiều).
Quy trình phân tích lưới
Thực hiện theo các bước sau trong khi giải quyết bất kỳ mạng hoặc mạch điện nào bằng phân tích Mesh.
Step 1 - Xác định meshes và dán nhãn các dòng điện lưới theo chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Step 2 - Quan sát cường độ dòng điện chạy qua từng phần tử về mặt lưới dòng điện.
Step 3 - Viết mesh equationscho tất cả các mắt lưới. Phương trình lưới thu được bằng cách áp dụng KVL đầu tiên và sau đó là định luật Ohm.
Step 4 - Giải các phương trình lưới thu được ở Bước 3 để có được mesh currents.
Bây giờ, chúng ta có thể tìm thấy dòng điện chạy qua bất kỳ phần tử nào và điện áp qua bất kỳ phần tử nào có trong mạng nhất định bằng cách sử dụng dòng điện lưới.
Thí dụ
Tìm hiệu điện thế trên điện trở 30 Ω bằng cách sử dụng Mesh analysis.
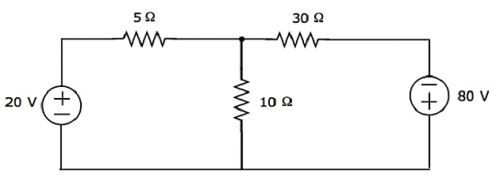
Step 1- Có hai mắt lưới trong đoạn mạch trên. Cácmesh currentsI 1 và I 2 được coi là theo chiều kim đồng hồ. Các dòng điện lưới này được thể hiện trong hình sau.
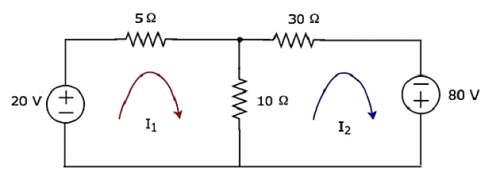
Step 2- Dòng điện lưới I 1 chạy qua nguồn hiệu điện thế 20 V và điện trở 5 Ω. Tương tự, dòng điện lưới I 2 chạy qua điện trở 30 Ω và nguồn điện áp -80 V. Nhưng, sự khác biệt của hai dòng điện lưới, I 1 và I 2 , chạy qua điện trở 10 Ω, vì nó là nhánh chung của hai mắt lưới.
Step 3 - Trong trường hợp này, chúng tôi sẽ nhận được two mesh equationsvì có hai mắt lưới trong mạch đã cho. Khi chúng ta viết phương trình lưới, giả sử dòng điện lưới của mắt lưới cụ thể đó lớn hơn tất cả các dòng điện lưới khác của mạch.
Các mesh equation của lưới đầu tiên là
$$20 - 5I_1 -10(I_1 - I_2) = 0$$
$$\Rightarrow 20 - 15I_1 + 10I_2 = 0$$
$$\Rightarrow 10I_2 = 15I_1 - 20$$
Chia phương trình trên với 5.
$$2I_2 = 3I_1 - 4$$
Nhân phương trình trên với 2.
$4I_2 = 6I_1 - 8$ Equation 1
Các mesh equation của lưới thứ hai là
$$-10(I_2 - I_1) - 30I_2 + 80 = 0$$
Chia phương trình trên với 10.
$$-(I_2 - I_1) - 3I_2 + 8 = 0$$
$$\Rightarrow -4I_2 + I_1 + 8 = 0$$
$4I_2 = I_1 + 8$ Equation 2
Step 4- Tìm dòng lưới I 1 và I 2 bằng cách giải phương trình 1 và phương trình 2.
Các số hạng bên trái của Phương trình 1 và Phương trình 2 giống nhau. Do đó, hãy cân bằng các số hạng bên phải của Phương trình 1 và Phương trình 2 để tìm giá trị của I 1 .
$$6I_1 - 8 = I_1 + 8$$
$$\Rightarrow 5I_1 = 16$$
$$\Rightarrow I_1 = \frac{16}{5} A$$
Thay thế giá trị I 1 trong Công thức 2.
$$4I_2 = \frac{16}{5} + 8$$
$$\Rightarrow 4I_2 = \frac{56}{5}$$
$$\Rightarrow I_2 = \frac{14}{5} A$$
Vì vậy, chúng tôi nhận được các dòng lưới I 1 và I 2 là$\mathbf{\frac{16}{5}}$ A và $\mathbf{\frac{14}{5}}$ A tương ứng.
Step 5- Dòng điện chạy qua điện trở 30 Ω không là gì khác ngoài dòng điện lưới I 2 và nó có giá trị bằng$\frac{14}{5}$ A. Bây giờ, chúng ta có thể tìm hiệu điện thế trên điện trở 30 Ω bằng cách sử dụng định luật Ohm.
$$V_{30 \Omega} = I_2 R$$
Thay các giá trị của I 2 và R vào phương trình trên.
$$V_{30 \Omega} = \lgroup \frac{14}{5} \rgroup 30$$
$$\Rightarrow V_{30 \Omega} = 84V$$
Do đó, điện áp trên điện trở 30 Ω của đoạn mạch đã cho là 84 V.
Note 1- Từ ví dụ trên, chúng ta có thể kết luận rằng chúng ta phải giải phương trình lưới 'm', nếu mạch điện có lưới 'm'. Đó là lý do tại sao chúng ta có thể chọn phân tích Mesh khi số lượng mắt lưới ít hơn số nút chính (trừ nút tham chiếu) của bất kỳ mạch điện nào.
Note 2 - Chúng ta có thể chọn phân tích Nodal hoặc phân tích Mesh, khi số lượng mắt lưới bằng số nút chính (trừ nút tham chiếu) trong bất kỳ mạch điện nào.
Nếu một mạch bao gồm hai hoặc nhiều phần tử thụ động giống nhau và được kết nối riêng với loại nối tiếp hoặc loại song song, thì chúng ta có thể thay thế chúng bằng một phần tử thụ động tương đương duy nhất. Do đó, mạch này được gọi làequivalent circuit.
Trong chương này, chúng ta hãy thảo luận về hai mạch tương đương sau đây.
- Dòng mạch tương đương
- Mạch tương đương song song
Dòng mạch tương đương
Nếu các phần tử thụ động tương tự được kết nối trong series, sau đó cùng một dòng điện sẽ chạy qua tất cả các phần tử này. Tuy nhiên, điện áp được chia cho từng phần tử.
Hãy xem xét những điều sau circuit diagram.
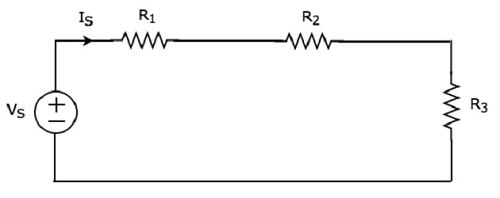
Nó có một nguồn điện áp duy nhất (V S ) và ba điện trở có các điện trở R 1 , R 2 và R 3 . Tất cả các yếu tố này được kết nối trong chuỗi. Dòng IS hiện tại chạy qua tất cả các yếu tố này.
Đoạn mạch trên chỉ có một mắt lưới. CácKVL equation xung quanh lưới này là
$$V_S = V_1 + V_2 + V_3$$
Người thay thế $V_1 = I_S R_1, \: V_2 = I_S R_2$ và $V_3 = I_S R_3$ trong phương trình trên.
$$V_S = I_S R_1 + I_S R_2 + I_S R_3$$
$$\Rightarrow V_S = I_S(R_1 + R_2 + R_3)$$
Phương trình trên có dạng $V_S = I_S R_{Eq}$ Ở đâu,
$$R_{Eq} = R_1 + R_2 + R_3$$
Các equivalent circuit diagram của mạch đã cho được hiển thị trong hình sau.
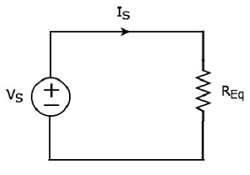
Điều đó có nghĩa là, nếu nhiều điện trở được mắc nối tiếp, thì chúng ta có thể thay thế chúng bằng một equivalent resistor. Điện trở của điện trở tương đương này bằng tổng các điện trở của tất cả các điện trở đó.
Note 1- Nếu cuộn cảm 'N' có độ tự cảm L 1 , L 2 , ..., L N mắc nối tiếp thìequivalent inductance sẽ là
$$L_{Eq} = L_1 + L_2 + ... + L_N$$
Note 2- Nếu các tụ 'N' có điện dung C 1 , C 2 , ..., C N mắc nối tiếp thìequivalent capacitance sẽ là
$$\frac{1}{C_{Eq}} = \frac{1}{C_1} + \frac{1}{C_2} + ... + \frac{1}{C_N}$$
Mạch tương đương song song
Nếu các phần tử thụ động tương tự được kết nối trong parallel, sau đó cùng một điện áp sẽ được duy trì trên mỗi phần tử. Nhưng, dòng điện chạy qua mỗi phần tử bị phân chia.
Hãy xem xét những điều sau circuit diagram.

Nó có một nguồn dòng điện (I S ) và ba điện trở có điện trở R 1 , R 2 và R 3 . Tất cả các yếu tố này được kết nối song song. Điện áp (V S ) có sẵn trên tất cả các phần tử này.
Mạch trên chỉ có một nút chính (P) trừ nút Đất. CácKCL equation tại nút chính này (P) là
$$I_S = I_1 + I_2 + I_3$$
Người thay thế $I_1 = \frac{V_S}{R_1}, \: I_2 = \frac{V_S}{R_2}$ và $I_3 = \frac{V_S}{R_3}$ trong phương trình trên.
$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} + \frac{V_S}{R_3}$$
$$\Rightarrow I_S = V_S \lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup$$
$$\Rightarrow V_S = I_S\left [ \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup} \right ]$$
Phương trình trên có dạng V S = I S R Eq trong đó,
$$R_{Eq} = \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup}$$
$$\frac{1}{R_{Eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$
Các equivalent circuit diagram của mạch đã cho được hiển thị trong hình sau.
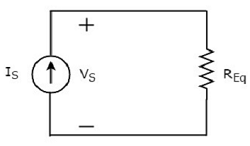
Điều đó có nghĩa là, nếu mắc song song nhiều điện trở thì ta có thể thay chúng bằng một điện trở tương đương. Sự kháng cự của điều nàyequivalent resistor bằng nghịch đảo của tổng nghịch đảo của mỗi điện trở của tất cả các điện trở đó.
Note 1- Nếu cuộn cảm 'N' có độ tự cảm L 1 , L 2 , ..., L N mắc song song thìequivalent inductance sẽ là
$$\frac{1}{L_{Eq}} = \frac{1}{L_1} + \frac{1}{L_2} + ... + \frac{1}{L_N}$$
Note 2- Nếu các tụ 'N' có điện dung C 1 , C 2 , ..., C N mắc song song thìequivalent capacitance sẽ là
$$C_{Eq} = C_1 + C_2 + ... + C_N$$
Trong chương trước, chúng ta đã thảo luận về các mạch tương đương của kết hợp nối tiếp và kết hợp song song riêng lẻ. Trong chương này, chúng ta hãy giải quyết một vấn đề ví dụ bằng cách xem xét cả hai chuỗi và kết hợp song song của các phần tử bị động tương tự.
Thí dụ
Hãy để chúng tôi tìm equivalent resistance qua các đầu cuối A & B của mạng điện sau.

Chúng ta sẽ nhận được điện trở tương đương trên các đầu cuối A & B bằng cách thu nhỏ mạng trên thành một điện trở duy nhất giữa hai đầu cuối đó. Đối với điều này, chúng ta phảiidentify the combination of resistors được kết nối ở dạng nối tiếp và dạng song song và sau đó tìm điện trở tương đương của dạng tương ứng trong mỗi bước.
Mạng điện đã cho là modified thành dạng sau như hình sau.
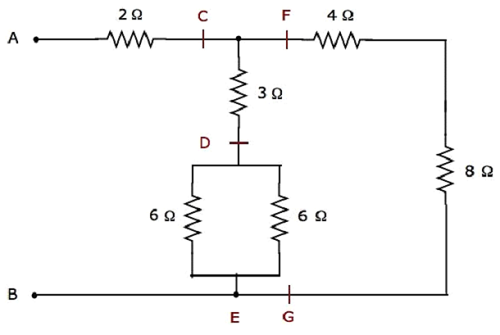
Trong hình trên, các chữ cái, C đến G, được sử dụng để ghi nhãn các thiết bị đầu cuối khác nhau.
Step 1 - Trong mạng trên, hai 6 Ω resistors được kết nối trong parallel. Vì vậy, điện trở tương đương giữa D & E sẽ là 3 Ω. Điều này có thể đạt được bằng cách đơn giản hóa sau đây.
$$R_{DE} = \frac{6 \times 6}{6 + 6} = \frac{36}{12} = 3 \Omega$$
Trong mạng trên, các điện trở 4 Ω và 8 Ω được kết nối trong series. Vì vậy, điện trở tương đương giữa F & G sẽ là 12 Ω. Điều này có thể đạt được bằng cách đơn giản hóa sau đây.
$$R_{FG} = 4 + 8 = 12 \Omega$$
Step 2 - Điện đơn giản network after Step 1 được hiển thị trong hình sau.
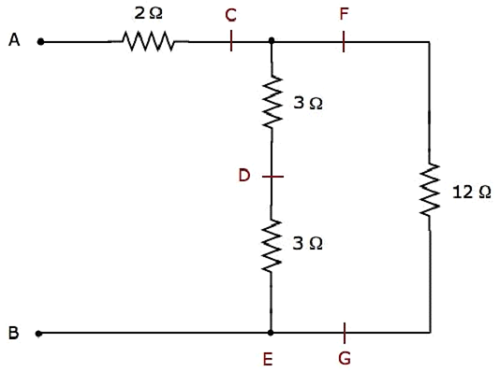
Trong mạng trên, hai 3 Ω resistors được kết nối trong series. Vì vậy, điện trở tương đương giữa C & E sẽ là6 Ω. Điều này có thể đạt được bằng cách đơn giản hóa sau đây.
$$R_{CE} = 3 + 3 = 6 \Omega$$
Step 3 - Điện đơn giản network after Step 2 được hiển thị trong hình sau.

Trong mạng trên, các điện trở 6 Ω và 12 Ω được kết nối trong parallel. Vì vậy, điện trở tương đương giữa C & B sẽ là 4 Ω. Điều này có thể đạt được bằng cách đơn giản hóa sau đây.
$$R_{CB} = \frac{6 \times 12}{6 + 12} = \frac{72}{18} = 4 \Omega$$
Step 4 - Điện đơn giản network after Step 3 được hiển thị trong hình sau.
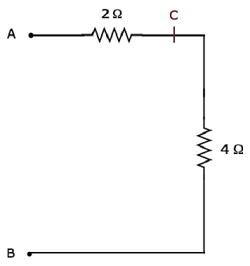
Trong mạng trên, các điện trở 2 Ω và 4 Ω được kết nối trong seriesgiữa các cực A & B. Vì vậy, điện trở tương đương giữa A & B sẽ là 6 Ω. Điều này có thể đạt được bằng cách đơn giản hóa sau đây.
$$R_{AB} = 2 + 4 = 6 \Omega$$
Do đó, điện trở tương đương giữa các đầu cuối A và B của mạng điện đã cho là 6 Ω.
Trong chương trước, chúng ta đã thảo luận về một vấn đề ví dụ liên quan đến điện trở tương đương. Ở đó, chúng tôi đã tính toánequivalent resistancegiữa các đầu cuối A & B của mạng điện đã cho một cách dễ dàng. Bởi vì, trong mỗi bước, chúng tôi nhận được sự kết hợp của các điện trở được kết nối ở dạng nối tiếp hoặc dạng song song.
Tuy nhiên, trong một số tình huống, rất khó để đơn giản hóa mạng bằng cách tiếp cận trước đây. Ví dụ, các điện trở được kết nối ở dạng tam giác (δ) hoặc dạng sao. Trong những tình huống như vậy, chúng ta phảiconvertmạng của một dạng này với dạng kia để đơn giản hóa nó hơn nữa bằng cách sử dụng kết hợp chuỗi hoặc kết hợp song song. Trong chương này, chúng ta hãy thảo luận vềDelta to Star Conversion.
Mạng Delta
Hãy xem xét những điều sau delta network như trong hình sau.
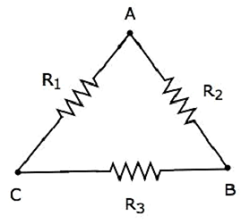
Các phương trình sau đại diện cho equivalent resistance giữa hai thiết bị đầu cuối của mạng delta, khi thiết bị đầu cuối thứ ba được giữ ở trạng thái mở.
$$R_{AB} = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$$
$$R_{BC} = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$$
$$R_{CA} = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$$
Mạng sao
Hình sau cho thấy equivalent star network tương ứng với mạng delta trên.
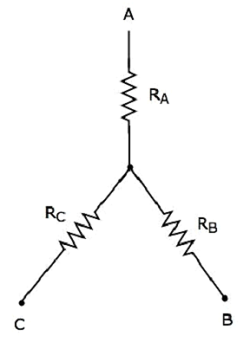
Các phương trình sau đại diện cho equivalent resistance giữa hai đầu cuối của mạng hình sao, khi đầu cuối thứ ba được giữ ở trạng thái mở.
$$R_{AB} = R_A + R_B$$
$$R_{BC} = R_B + R_C$$
$$R_{CA} = R_C + R_A$$
Điện trở mạng hình sao về kháng cự mạng Delta
Chúng ta sẽ nhận được các phương trình sau đây bằng cách cân bằng các số hạng bên phải của các phương trình trên mà các số hạng bên trái giống nhau.
$R_A + R_B = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$ Equation 1
$R_B + R_C = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$ Equation 2
$R_C + R_A = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$ Equation 3
Bằng cách cộng ba phương trình trên, chúng ta sẽ nhận được
$$2(R_A + R_B + R_C) = \frac{2(R_1 R_2 + R_2 R_3 + R_3 R_1)}{R_1 + R_2 + R_3}$$
$\Rightarrow R_A + R_B + R_C = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3}$ Equation 4
Trừ phương trình 2 khỏi phương trình 4.
$R_A + R_B + R_C - (R_B + R_C) = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3} - \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$
$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$
Bằng cách trừ Phương trình 3 khỏi Phương trình 4, chúng ta sẽ nhận được
$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$
Bằng cách trừ Phương trình 1 khỏi Phương trình 4, chúng ta sẽ nhận được
$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$
Bằng cách sử dụng các quan hệ trên, chúng ta có thể tìm thấy các điện trở của mạng sao từ các điện trở của mạng delta. Bằng cách này, chúng ta có thể chuyển đổi mộtdelta network thành một star network.
Thí dụ
Hãy để chúng tôi tính toán resistances of star network, tương đương với mạng delta như trong hình sau.
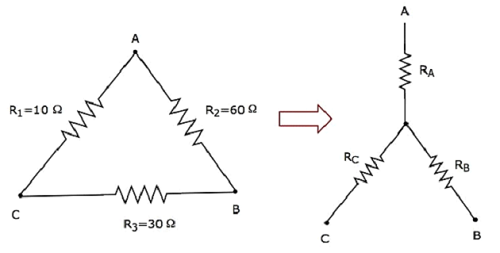
Đưa ra resistances of delta networknhư R 1 = 10 Ω, R 2 = 60 Ω và R 3 = 30 Ω.
Chúng ta biết các quan hệ sau đây của các điện trở của mạng hình sao về điện trở của mạng delta.
$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$
$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$
$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$
Thay các giá trị của R 1 , R 2 và R 3 vào các phương trình trên.
$$R_A = \frac{10 \times 60}{10 +60+30} = \frac{600}{100} = 6\Omega$$
$$R_B = \frac{60 \times 30}{10 +60+30} = \frac{1800}{100} = 18\Omega$$
$$R_C = \frac{30 \times 10}{10 +60+30} = \frac{300}{100} = 3\Omega$$
Vì vậy, chúng tôi nhận được các điện trở của mạng sao là RA = 6 Ω, RB = 18 Ω và RC = 3 Ω, tương đương với các điện trở của mạng delta đã cho.
Trong chương trước, chúng ta đã thảo luận về việc chuyển đổi mạng delta thành mạng sao tương đương. Bây giờ, chúng ta hãy thảo luận về việc chuyển đổi mạng sao thành mạng đồng bằng tương đương. Chuyển đổi này được gọi làStar to Delta Conversion.
Trong chương trước, chúng ta đã có resistances of star network từ mạng delta với tư cách là
$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$ Equation 1
$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$ Equation 2
$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$ Equation 3
Điện trở mạng Delta xét về Điện trở mạng hình sao
Chúng ta hãy thao tác các phương trình trên để có được điện trở của mạng delta về điện trở của mạng hình sao.
Multiply mỗi bộ hai phương trình và sau đó add.
$$R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2^2 R_3 + R_2 R_3^2 R_1 + R_3 R_1^2 R_2}{(R_1 + R_2 + R_3)^2}$$
$$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$$
$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3}$ Equation 4
Bằng cách chia Phương trình 4 với Phương trình 2, chúng ta sẽ được
$$\frac{R_A R_B + R_B R_C + R_C R_A}{R_B} = R_1$$
$$\Rightarrow R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
Bằng cách chia Phương trình 4 với Phương trình 3, chúng ta sẽ được
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
Bằng cách chia Phương trình 4 với Phương trình 1, chúng ta sẽ được
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
Bằng cách sử dụng các quan hệ trên, chúng ta có thể tìm thấy các điện trở của mạng delta từ các điện trở của mạng hình sao. Bằng cách này, chúng tôi có thể chuyển đổistar network into delta network.
Thí dụ
Hãy để chúng tôi tính toán resistances of delta network, tương đương với mạng hình sao như trong hình sau.
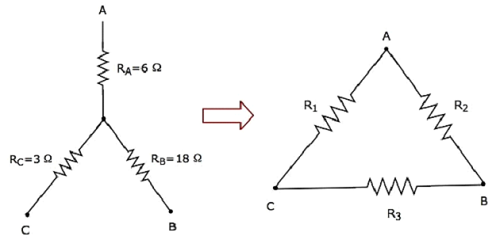
Đưa ra resistances of star networknhư R A = 6 Ω, R B = 18 Ω và R C = 3 Ω .
Chúng tôi biết các mối quan hệ sau của resistances of delta network về điện trở của mạng hình sao.
$$R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
Thay các giá trị của R A , R B và R C vào các phương trình trên.
$$R_1 = 3 + 6 + \frac{3 \times 6}{18} = 9 + 1 = 10 \Omega$$
$$R_2 = 6 + 18 + \frac{6 \times 18}{3} = 24 + 36 = 60 \Omega$$
$$R_3 = 18 + 3 + \frac{18 \times 3}{6} = 21 + 9 = 30 \Omega$$
Vì vậy, chúng tôi nhận được các điện trở của mạng delta là R1 = 10 Ω, R2 = 60 Ω và R3 = 30 Ω, tương đương với các điện trở của mạng hình sao đã cho.
Cấu trúc liên kết mạng là một biểu diễn đồ họa của các mạch điện. Nó rất hữu ích để phân tích các mạch điện phức tạp bằng cách chuyển đổi chúng thành đồ thị mạng. Cấu trúc liên kết mạng còn được gọi làGraph theory.
Thuật ngữ cơ bản của cấu trúc liên kết mạng
Bây giờ, chúng ta hãy thảo luận về các thuật ngữ cơ bản liên quan đến cấu trúc liên kết mạng này.
Đồ thị
Biểu đồ mạng được gọi đơn giản là graph. Nó bao gồm một tập hợp các nút được kết nối bởi các nhánh. Trong đồ thị, một nút là điểm chung của hai hoặc nhiều nhánh. Đôi khi, chỉ một nhánh duy nhất có thể kết nối với nút. Nhánh là một đoạn thẳng nối hai nút.
Bất kỳ mạch điện hoặc mạng nào cũng có thể được chuyển đổi thành tương đương của nó graphbằng cách thay thế các phần tử thụ động và nguồn điện áp bị ngắn mạch và các nguồn dòng điện bị hở mạch. Điều đó có nghĩa là, các đoạn thẳng trong biểu đồ biểu diễn các nhánh tương ứng với các phần tử thụ động hoặc các nguồn điện áp của mạch điện.
Thí dụ
Hãy để chúng tôi xem xét những điều sau electric circuit.
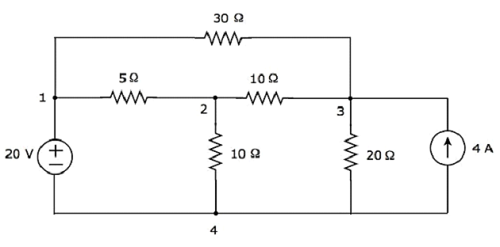
Trong đoạn mạch trên, có four principal nodes và những người đó được gắn nhãn 1, 2, 3 và 4. Có seven branches Trong đoạn mạch trên, trong đó một nhánh chứa nguồn điện áp 20 V, nhánh khác chứa nguồn dòng 4 A và năm nhánh còn lại chứa các điện trở có điện trở lần lượt là 30 Ω, 5 Ω, 10 Ω, 10 Ω và 20 Ω.
Một tương đương graph ứng với mạch điện trên được biểu diễn trong hình sau.
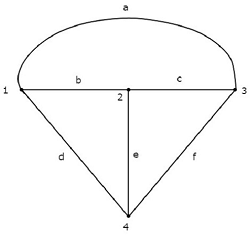
Trong biểu đồ trên, có four nodesvà chúng được gắn nhãn tương ứng là 1, 2, 3 & 4. Chúng giống như của các nút chính trong mạch điện. Cósix branches trong đồ thị trên và chúng được đánh dấu lần lượt là a, b, c, d, e & f.
Trong trường hợp này, chúng tôi có one branch less trong đồ thị vì nguồn 4 A làm mạch hở, đồng thời biến đổi điện trường thành đồ thị tương đương của nó.
Từ ví dụ này, chúng ta có thể kết luận những điểm sau:
Các number of nodes hiện trong đồ thị sẽ bằng số nút chính có trong mạch điện.
Các number of branches hiện trong một đồ thị sẽ nhỏ hơn hoặc bằng số nhánh có trong một mạch điện.
Các loại đồ thị
Sau đây là các loại đồ thị:
- Biểu đồ được kết nối
- Đồ thị không kết nối
- Đồ thị hướng
- Đồ thị vô hướng
Bây giờ, chúng ta hãy thảo luận từng đồ thị một.
Biểu đồ được kết nối
Nếu tồn tại ít nhất một nhánh giữa bất kỳ nút nào trong số hai nút của biểu đồ, thì nó được gọi là connected graph. Điều đó có nghĩa là, mỗi nút trong biểu đồ được kết nối sẽ có một hoặc nhiều nhánh được kết nối với nó. Vì vậy, không có nút nào sẽ hiển thị là bị cô lập hoặc tách biệt.
Biểu đồ được hiển thị trong Ví dụ trước là một connected graph. Ở đây, tất cả các nút được kết nối bởi ba nhánh.
Đồ thị không kết nối
Nếu tồn tại ít nhất một nút trong biểu đồ mà vẫn không được kết nối bởi một nhánh chẵn, thì nó được gọi là unconnected graph. Vì vậy, sẽ có một hoặc nhiều nút cô lập trong một đồ thị không được kết nối.
Hãy xem xét đồ thị được hiển thị trong hình sau.
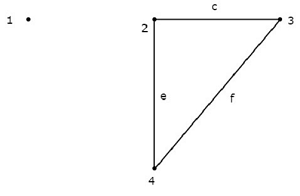
Trong biểu đồ này, các nút 2, 3 và 4 được nối với nhau bằng hai nhánh. Tuy nhiên, thậm chí không có một nhánh nào được kết nối vớinode 1. Vì vậy, nút 1 trở thành mộtisolated node. Do đó, biểu đồ trên là mộtunconnected graph.
Đồ thị hướng
Nếu tất cả các nhánh của biểu đồ được biểu diễn bằng các mũi tên, thì biểu đồ đó được gọi là directed graph. Các mũi tên này chỉ ra hướng của dòng điện trong mỗi nhánh. Do đó, biểu đồ này còn được gọi làoriented graph.
Hãy xem xét đồ thị được hiển thị trong hình sau.
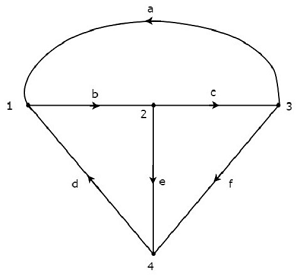
Trong đồ thị trên, chiều của dòng điện được biểu diễn bằng một mũi tên trong mỗi nhánh. Do đó, nó là mộtdirected graph.
Đồ thị vô hướng
Nếu các nhánh của biểu đồ không được biểu diễn bằng các mũi tên, thì biểu đồ đó được gọi là undirected graph. Vì không có hướng của dòng điện, đồ thị này còn được gọi làunoriented graph.
Biểu đồ được hiển thị trong Ví dụ đầu tiên của chương này là một unoriented graph, bởi vì không có mũi tên nào trên các nhánh của biểu đồ đó.
Subgraph và các loại của nó
Một phần của biểu đồ được gọi là subgraph. Chúng tôi nhận được đồ thị con bằng cách loại bỏ một số nút và / hoặc nhánh của một đồ thị nhất định. Vì vậy, số lượng nhánh và / hoặc nút của một đồ thị con sẽ ít hơn số lượng của đồ thị gốc. Do đó, chúng ta có thể kết luận rằng một đồ thị con là một tập hợp con của đồ thị.
Sau đây là two types trong số các đồ thị con.
- Tree
- Co-Tree
Cây
Cây là một đồ thị con được kết nối của một đồ thị đã cho, chứa tất cả các nút của đồ thị. Tuy nhiên, không nên có bất kỳ vòng lặp nào trong đồ thị con đó. Cành cây được gọi làtwigs.
Hãy xem xét những điều sau connected subgraph của đồ thị, được hiển thị trong Ví dụ ở đầu chương này.
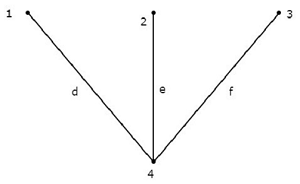
Đồ thị con được kết nối này chứa tất cả bốn nút của đồ thị đã cho và không có vòng lặp. Do đó, nó là mộtTree.
Cây này chỉ có ba nhánh trong số sáu nhánh của biểu đồ đã cho. Bởi vì, nếu ta xét nhánh chẵn của các nhánh còn lại của đồ thị thì trong đồ thị con liên thông trên sẽ có một vòng lặp. Khi đó, đồ thị con được kết nối kết quả sẽ không phải là Cây.
Từ Cây trên, chúng ta có thể kết luận rằng number of branches có mặt trong Cây phải bằng n - 1 trong đó 'n' là số nút của đồ thị đã cho.
Cây đồng
Co-Tree là một đồ thị con, được hình thành với các nhánh bị loại bỏ trong khi tạo thành một Cây. Do đó, nó được gọi làComplementcủa một cây. Với mỗi Cây, sẽ có một Cây cùng loại tương ứng và các nhánh của nó được gọi làlinkshoặc hợp âm. Nói chung, các liên kết được biểu diễn bằng các đường chấm.
Các Co-Tree tương ứng với Cây trên được thể hiện trong hình sau.
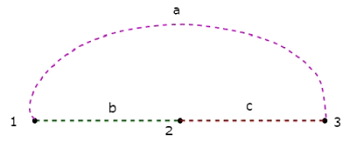
Co-Tree này chỉ có ba nút thay vì bốn nút của đồ thị đã cho, bởi vì Nút 4 được tách biệt với Co-Tree ở trên. Do đó, Co-Tree không cần phải là một đồ thị con được kết nối. Cây Co-Tree này có ba nhánh và chúng tạo thành một vòng lặp.
Các number of brancheshiện diện trong một cây đồng sẽ bằng hiệu giữa số nhánh của một đồ thị nhất định và số nhánh cây. Về mặt toán học, nó có thể được viết là
$$l = b - (n - 1)$$
$$l = b - n + 1$$
Ở đâu,
- l là số lượng liên kết.
- b là số nhánh có trong một đồ thị nhất định.
- n là số lượng nút có trong một đồ thị nhất định.
Nếu chúng ta kết hợp một Cây và một Cây tương ứng của nó, thì chúng ta sẽ nhận được original graph như hình bên dưới.
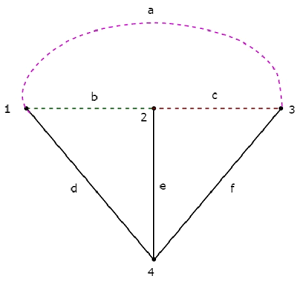
Các nhánh Cây d, e & f được biểu diễn bằng các đường liền nét. Các nhánh Co-Tree a, b & c được biểu diễn bằng các nét đứt.
Trong chương trước, chúng ta đã thảo luận về cách biến đổi một mạch điện thành một đồ thị tương đương. Bây giờ, chúng ta hãy thảo luận về Ma trận cấu trúc liên kết mạng hữu ích để giải quyết bất kỳ vấn đề mạng hoặc mạch điện nào bằng cách sử dụng các đồ thị tương đương của chúng.
Ma trận liên kết với đồ thị mạng
Sau đây là ba ma trận được sử dụng trong lý thuyết Đồ thị.
- Ma trận liên thuộc
- Ma trận vòng lặp cơ bản
- Ma trận bộ cắt cơ bản
Ma trận liên thuộc
Ma trận tỷ lệ ngẫu nhiên biểu diễn đồ thị của một mạch điện hoặc mạng điện nhất định. Do đó, có thể vẽ đồ thị của cùng một mạch điện hoặc mạng điện từincidence matrix.
Chúng ta biết rằng đồ thị bao gồm một tập hợp các nút và chúng được nối với nhau bằng một số nhánh. Vì vậy, kết nối của các nhánh với một nút được gọi là tỷ lệ mắc. Ma trận tỷ lệ được biểu diễn bằng chữ A. Nó còn được gọi là ma trận tỷ lệ nút đến nhánh hoặcnode incidence matrix.
Nếu có 'n' nút và nhánh 'b' có trong directed graph, thì ma trận tỷ lệ sẽ có 'n' hàng và 'b' cột. Ở đây, các hàng và cột tương ứng với các nút và nhánh của đồ thị có hướng. Vì thếorder ma trận tỷ lệ sẽ là n × b.
Các elements of incidence matrix sẽ có một trong ba giá trị này, +1, -1 và 0.
Nếu dòng nhánh rời khỏi một nút đã chọn, thì giá trị của phần tử sẽ là +1.
Nếu dòng điện nhánh đi vào một nút đã chọn, thì giá trị của phần tử sẽ là -1.
Nếu dòng điện nhánh không đi vào một nút đã chọn hoặc không rời khỏi một nút đã chọn, thì giá trị của phần tử sẽ là 0.
Quy trình tìm Ma trận Tỷ lệ
Thực hiện theo các bước sau để tìm ma trận tỷ lệ của đồ thị có hướng.
Chọn một nút tại một thời điểm của đồ thị có hướng đã cho và điền liên tiếp các giá trị của các phần tử của ma trận tỷ lệ tương ứng với nút đó.
Lặp lại bước trên cho tất cả các nút của đồ thị có hướng đã cho.
Thí dụ
Hãy xem xét những điều sau directed graph.

Các incidence matrix tương ứng với đồ thị có hướng trên sẽ là
$$A = \begin{bmatrix}-1 & 1 & 0 & -1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \\0 & 0 & 0 & 1 & -1 & -1 \end{bmatrix}$$
Các hàng và cột của ma trận trên đại diện cho các nút và các nhánh của đồ thị có hướng đã cho. Bậc của ma trận tỷ lệ này là 4 × 6.
Bằng cách quan sát ma trận tỷ lệ ở trên, chúng ta có thể kết luận rằng summationcủa các phần tử cột của ma trận tỷ lệ bằng không. Điều đó có nghĩa là, một dòng điện nhánh rời khỏi một nút và chỉ đi vào một nút duy nhất khác.
Note- Nếu đồ thị đã cho là kiểu không có hướng, thì chuyển nó thành đồ thị có hướng bằng cách biểu diễn các mũi tên trên mỗi nhánh của nó. Chúng ta có thể xem xét hướng tùy ý của dòng điện trong mỗi nhánh.
Ma trận vòng lặp cơ bản
Vòng lặp cơ bản hoặc f-looplà một vòng lặp, chỉ chứa một liên kết và một hoặc nhiều nhánh rẽ. Vì vậy, số vòng lặp f sẽ bằng số liên kết. Ma trận vòng lặp cơ bản được biểu diễn bằng chữ B. Nó còn được gọi làfundamental circuit matrixvà ma trận Tie-set. Ma trận này đưa ra mối quan hệ giữa dòng điện nhánh và dòng điện liên kết.
Nếu có 'n' nút và nhánh 'b' có trong directed graph, khi đó số liên kết có trong cây đồng ứng với cây đã chọn của đồ thị đã cho sẽ là b-n + 1.
Vì vậy, ma trận vòng lặp cơ bản sẽ có hàng 'b-n + 1' và cột 'b'. Ở đây, các hàng và cột tương ứng với các liên kết của đồng cây và các nhánh của đồ thị đã cho. Do đó, thứ tự của ma trận vòng lặp cơ bản sẽ là(b - n + 1) × b.
Các elements of fundamental loop matrix sẽ có một trong ba giá trị này, +1, -1 và 0.
Giá trị của phần tử sẽ được +1 cho liên kết của vòng lặp f đã chọn.
Giá trị của các phần tử sẽ là 0 đối với các liên kết và nhánh còn lại, không thuộc vòng lặp f đã chọn.
Nếu hướng của dòng điện nhánh của vòng f đã chọn giống với hướng của dòng liên kết f vòng, thì giá trị của phần tử sẽ là +1.
Nếu hướng của dòng điện nhánh của vòng f được chọn ngược với chiều của dòng liên kết f vòng, thì giá trị của phần tử sẽ là -1.
Quy trình tìm Ma trận vòng lặp cơ bản
Thực hiện theo các bước sau để tìm ma trận vòng cơ bản của đồ thị có hướng đã cho.
Chọn một cây của đồ thị có hướng cho trước.
Bằng cách bao gồm một liên kết tại một thời điểm, chúng ta sẽ nhận được một vòng lặp f. Điền các giá trị của các phần tử tương ứng với vòng lặp f này trong một hàng của ma trận vòng lặp cơ bản.
Lặp lại bước trên cho tất cả các liên kết.
Thí dụ
Hãy xem cây sau của directed graph, được xem xét cho ma trận tỷ lệ.

Cây trên gồm ba nhánh d, e & f. Do đó, các nhánh a, b & c sẽ là các liên kết của Cây đồng ứng với Cây trên. Bằng cách bao gồm một liên kết tại một thời điểm đến Cây ở trên, chúng tôi sẽ nhận được mộtf-loop. Vì vậy, sẽ có baf-loops, vì có ba liên kết. Ba vòng lặp f này được thể hiện trong hình sau.
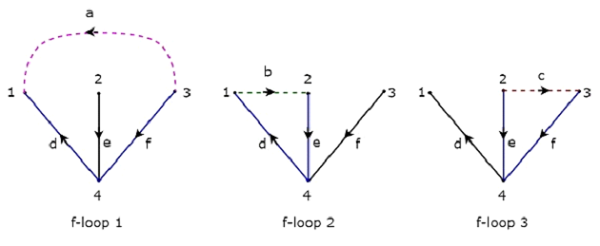
Trong hình trên, các nhánh, được biểu diễn bằng các đường màu tạo thành các vòng f. Chúng ta sẽ nhận được các giá trị phần tử khôn ngoan hàng của ma trận Tie-set từ mỗi vòng lặp f. NênTieset matrix trong số các Cây được xem xét ở trên sẽ là
$$B = \begin{bmatrix}1 & 0 & 0 & -1 & 0 & -1\\0 & 1 & 0 & 1 & 1 & 0\\0 & 0 & 1 & 0 & -1 & 1 \end{bmatrix}$$
Các hàng và cột của ma trận trên đại diện cho các liên kết và các nhánh của đồ thị có hướng cho trước. Bậc của ma trận tỷ lệ này là 3 × 6.
Các number of Fundamental loop matricescủa một biểu đồ có hướng sẽ bằng số Cây của biểu đồ có hướng đó. Bởi vì, mỗi Cây sẽ có một ma trận vòng lặp Cơ bản.
Ma trận tổng hợp cơ bản
Bộ cắt cơ bản hoặc f-cut setlà số nhánh tối thiểu được loại bỏ khỏi đồ thị theo cách mà đồ thị ban đầu sẽ trở thành hai đồ thị con biệt lập. Bộ f-cut chỉ chứaone twigvà một hoặc nhiều liên kết. Vì vậy, số f bộ cắt sẽ bằng số cành cây.
Fundamental cut set matrix được biểu diễn bằng chữ C. Ma trận này cung cấp mối quan hệ giữa điện áp nhánh và điện áp nhánh.
Nếu có 'n' nút và nhánh 'b' có trong directed graph, khi đó số cành cây có trong một Cây được chọn của đồ thị đã cho sẽ là n-1. Vì vậy, ma trận tập hợp cắt cơ bản sẽ có 'n-1' hàng và 'b' cột. Ở đây, các hàng và cột tương ứng với các nhánh của cây và nhánh đã chọn của biểu đồ đã cho. Vì thếorder của ma trận tập hợp cắt cơ bản sẽ là (n-1) × b.
Các elements of fundamental cut set matrix sẽ có một trong ba giá trị này, +1, -1 và 0.
Giá trị của phần tử sẽ được +1 cho nhánh của f-cutset đã chọn.
Giá trị của các phần tử sẽ là 0 đối với các nhánh và liên kết còn lại, không thuộc tập cắt f đã chọn.
Nếu hướng của dòng điện liên kết của bộ cắt f đã chọn giống với hướng của dòng điện nhánh bộ cắt f, thì giá trị của phần tử sẽ là +1.
Nếu hướng của dòng điện liên kết của bộ cắt f đã chọn ngược với hướng của dòng điện cắt bộ f, thì giá trị của phần tử sẽ là -1.
Quy trình tìm Ma trận tổng hợp cơ bản
Thực hiện theo các bước sau để tìm ma trận tập cắt cơ bản của đồ thị có hướng đã cho.
Chọn một cây đồ thị có hướng cho trước và biểu diễn các liên kết bằng các đường chấm.
Bằng cách loại bỏ một cành cây và các liên kết cần thiết cùng một lúc, chúng ta sẽ nhận được một bộ f-cut. Điền các giá trị của các phần tử tương ứng với tập cắt f này vào một hàng của ma trận tập cắt cơ bản.
Lặp lại bước trên cho tất cả các cành cây.
Thí dụ
Coi như directed graph , mà chúng ta đã thảo luận trong phần ma trận tỷ lệ. Chọn các nhánh d, e & f của đồ thị có hướng này dưới dạng các nhánh. Vì vậy, các nhánh còn lại a, b & c của đồ thị có hướng này sẽ là các liên kết.
Các twigs d, e & f được biểu diễn bằng các đường liền nét và links a, b & c được biểu diễn bằng các đường chấm trong hình sau.
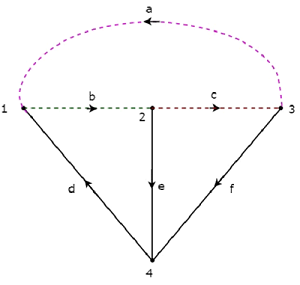
Bằng cách loại bỏ một cành cây và các liên kết cần thiết cùng một lúc, chúng ta sẽ nhận được một bộ f-cut. Vì vậy, sẽ có ba bộ cắt f, vì có ba nhánh. Ba cái nàyf-cut sets được hiển thị trong hình sau.

Chúng ta sẽ có ba tập cắt f bằng cách loại bỏ một tập hợp các nhánh và liên kết của C 1 , C 2 và C 3 . Chúng ta sẽ nhận được các giá trị phần tử khôn ngoan hàng của ma trận tập cắt cơ bản từ mỗi tập cắt f. Nênfundamental cut set matrix trong số các Cây được xem xét ở trên sẽ là
$$C = \begin{bmatrix}1 & -1 & 0 & 1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \end{bmatrix}$$
Các hàng và cột của ma trận trên đại diện cho các nhánh và nhánh của đồ thị có hướng đã cho. Bậc của ma trận tập cắt cơ bản này là 3 × 6.
Các number of Fundamental cut set matricescủa một biểu đồ có hướng sẽ bằng số Cây của biểu đồ có hướng đó. Bởi vì, mỗi Cây sẽ có một ma trận cắt cơ bản.
Superposition theoremdựa trên khái niệm tuyến tính giữa phản ứng và kích thích của một mạch điện. Nó nói rằng phản ứng trong một nhánh cụ thể của mạch tuyến tính khi nhiều nguồn độc lập hoạt động cùng một lúc tương đương với tổng các phản hồi do mỗi nguồn độc lập hoạt động tại một thời điểm.
Trong phương pháp này, chúng tôi sẽ chỉ xem xét one independent sourcetại một thời điểm. Vì vậy, chúng ta phải loại bỏ các nguồn độc lập còn lại khỏi mạch. Chúng ta có thể loại bỏ các nguồn điện áp bằng cách nối tắt hai đầu nối của chúng và tương tự, các nguồn dòng điện bằng cách mở hai đầu nối của chúng.
Do đó, chúng ta cần tìm phản hồi trong một nhánh cụ thể ‘n’ timesnếu có 'n' nguồn độc lập. Đáp ứng trong một nhánh cụ thể có thể là dòng điện chạy qua nhánh đó hoặc điện áp trên nhánh đó.
Quy trình của Định lý chồng chất
Thực hiện theo các bước sau để tìm phản ứng trong một nhánh cụ thể bằng cách sử dụng định lý chồng chất.
Step 1 - Tìm phản hồi trong một nhánh cụ thể bằng cách xem xét một nguồn độc lập và loại bỏ các nguồn độc lập còn lại có trong mạng.
Step 2 - Lặp lại Bước 1 cho tất cả các nguồn độc lập có trong mạng.
Step 3 - Thêm tất cả các phản hồi để có được phản hồi tổng thể trong một nhánh cụ thể khi tất cả các nguồn độc lập đều có trong mạng.
Thí dụ
Tìm cường độ dòng điện chạy qua điện trở 20 Ω của đoạn mạch sau sử dụng superposition theorem.
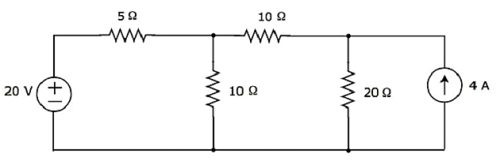
Step 1 - Ta tìm cường độ dòng điện chạy qua điện trở 20 Ω bằng cách chỉ xét 20 V voltage source. Trong trường hợp này, chúng ta có thể loại bỏ nguồn dòng 4 A bằng cách làm hở mạch của nó. Sơ đồ mạch sửa đổi được hiển thị trong hình sau.

Chỉ có một nút chính ngoại trừ Ground trong mạch trên. Vì vậy, chúng ta có thể sử dụngnodal analysisphương pháp. Điện áp nút V 1 được đánh dấu trong hình sau. Ở đây, V 1 là điện áp từ nút 1 đối với mặt đất.
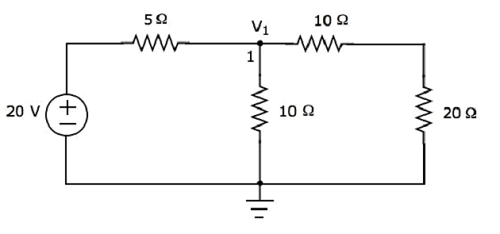
Các nodal equation tại nút 1 là
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1}{10 + 20} = 0$$
$$\Rightarrow \frac{6V_1 - 120 + 3V_1 + V_1}{30} = 0$$
$$\Rightarrow 10V_1 = 120$$
$$\Rightarrow V_1 = 12V$$
Các current flowing through 20 Ω resistor có thể được tìm thấy bằng cách đơn giản hóa sau đây.
$$I_1 = \frac{V_1}{10 + 20}$$
Thay giá trị của V 1 vào phương trình trên.
$$I_1 = \frac{12}{10 + 20} = \frac{12}{30} = 0.4 A$$
Do đó, cường độ dòng điện chạy qua điện trở 20 Ω là 0.4 A, khi chỉ coi nguồn điện áp 20 V.
Step 2 - Ta tìm cường độ dòng điện chạy qua điện trở 20 Ω bằng cách chỉ xét 4 A current source. Trong trường hợp này, chúng ta có thể loại bỏ nguồn điện áp 20 V bằng cách làm ngắn mạch nó. Sơ đồ mạch sửa đổi được hiển thị trong hình sau.
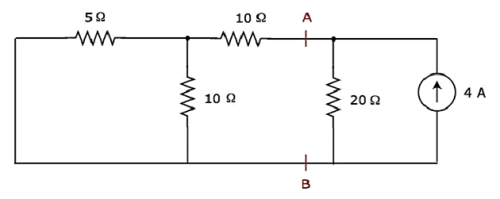
Trong đoạn mạch trên, có ba điện trở ở bên trái của các đầu nối A & B. Chúng ta có thể thay thế các điện trở này bằng một equivalent resistor. Ở đây, các điện trở 5 Ω & 10 Ω được kết nối song song và toàn bộ kết hợp mắc nối tiếp với điện trở 10 Ω.
Các equivalent resistance ở bên trái của các nhà ga A & B sẽ là
$$R_{AB} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$
Sơ đồ mạch đơn giản được hiển thị trong hình sau.
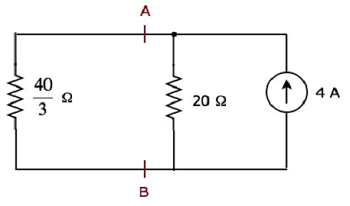
Chúng ta có thể tìm thấy dòng điện chạy qua điện trở 20 Ω, bằng cách sử dụng current division principle.
$$I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$
Người thay thế $I_S = 4A,\: R_1 = \frac{40}{3} \Omega$ và $R_2 = 20 \Omega$ trong phương trình trên.
$$I_2 = 4 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup = 4 \lgroup \frac{40}{100} \rgroup = 1.6 A$$
Do đó, cường độ dòng điện chạy qua điện trở 20 Ω là 1.6 A, khi chỉ coi nguồn dòng 4 A.
Step 3 - Ta sẽ nhận được dòng điện chạy qua điện trở 20 Ω của đoạn mạch đã cho bằng cách thực hiện addition of two currents mà chúng ta đã đạt được ở bước 1 và bước 2. Về mặt toán học, nó có thể được viết là
$$I = I_1 + I_2$$
Thay vào đó, giá trị của I 1 và I 2 trong phương trình trên.
$$I = 0.4 + 1.6 = 2 A$$
Do đó cường độ dòng điện chạy qua điện trở 20 Ω của đoạn mạch đã cho là 2 A.
Note - Chúng ta không thể áp dụng định lý chồng chất trực tiếp để tìm lượng powerđược phân phối cho bất kỳ điện trở nào có trong mạch tuyến tính, chỉ bằng cách thực hiện việc cộng công suất được phân phối cho điện trở đó do mỗi nguồn độc lập. Thay vào đó, chúng ta có thể tính toán tổng dòng điện chạy qua hoặc điện áp trên điện trở đó bằng cách sử dụng định lý chồng chất và từ đó, chúng ta có thể tính toán lượng điện năng cung cấp cho điện trở đó bằng cách sử dụng$I^2 R$ hoặc là $\frac{V^2}{R}$.
Thevenin’s theoremtrạng thái rằng bất kỳ mạng hoặc mạch tuyến tính hai đầu cuối có thể được biểu diễn bằng mạng hoặc mạch tương đương, bao gồm nguồn điện áp mắc nối tiếp với một điện trở. Nó được gọi là mạch tương đương của Thevenin. Mạch tuyến tính có thể chứa các nguồn độc lập, nguồn phụ thuộc và điện trở.
Nếu mạch chứa nhiều nguồn độc lập, nguồn phụ thuộc và điện trở, thì đáp ứng trong một phần tử có thể dễ dàng tìm thấy bằng cách thay thế toàn bộ mạng ở bên trái của phần tử đó bằng một Thevenin’s equivalent circuit.
Các response in an element có thể là điện áp trên phần tử đó, dòng điện chạy qua phần tử đó hoặc công suất tiêu tán trên phần tử đó.
Khái niệm này được minh họa trong các hình sau.
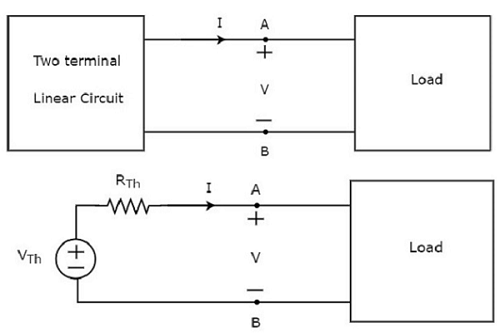
Thevenin’s equivalent circuitgiống nguồn điện áp thực tế. Do đó, nó có một nguồn điện áp nối tiếp với một điện trở.
Nguồn điện áp có trong mạch tương đương của Thevenin được gọi là điện áp tương đương của Thevenin hoặc đơn giản Thevenin’s voltage, VTh.
Điện trở hiện diện trong mạch tương đương của Thevenin được gọi là điện trở tương đương của Thevenin hoặc đơn giản là Thevenin’s resistor, RTh.
Phương pháp tìm mạch tương đương của Thevenin
Có ba phương pháp để tìm mạch tương đương của Thevenin. Dựa vàotype of sourcescó trong mạng, chúng ta có thể chọn một trong ba phương pháp này. Bây giờ, chúng ta hãy thảo luận về hai phương pháp một. Chúng ta sẽ thảo luận về phương pháp thứ ba trong chương tiếp theo.
Phương pháp 1
Làm theo các bước sau để tìm mạch tương đương của Thevenin, khi chỉ sources of independent type đang có mặt.
Step 1 - Xem xét sơ đồ mạch bằng cách mở các đầu nối đối với mạch tương đương của Thevenin sẽ được tìm thấy.
Step 2 - Tìm điện áp của Thevenin VTh qua các đầu cuối hở của đoạn mạch trên.
Step 3 - Tìm sự kháng cự của Thevenin RTh qua các đầu cuối mở của mạch trên bằng cách loại bỏ các nguồn độc lập có trong nó.
Step 4 - Vẽ Thevenin’s equivalent circuitbằng cách mắc nối tiếp điện áp V Th của Thevenin với điện trở của Thevenin R Th .
Bây giờ, chúng ta có thể tìm thấy phản ứng trong một phần tử nằm ở phía bên phải của mạch tương đương của Thevenin.
Thí dụ
Tìm cường độ dòng điện chạy qua điện trở 20 Ω bằng cách tìm Thevenin’s equivalent circuit ở bên trái của thiết bị đầu cuối A và B.
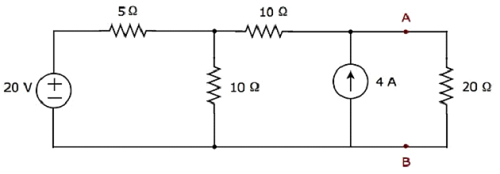
Step 1 - Để tìm mạch tương đương của Thevenin ở phía bên trái của đầu cuối A & B, chúng ta nên loại bỏ điện trở 20 Ω khỏi mạng bằng cách opening the terminals A & B. Sơ đồ mạch sửa đổi được hiển thị trong hình sau.
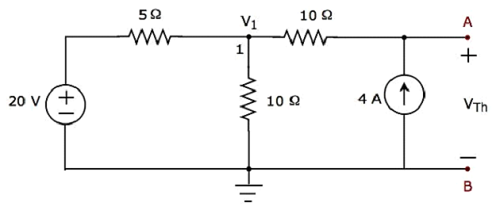
Step 2 - Tính toán của Thevenin’s voltage VTh.
Chỉ có một nút chính ngoại trừ Ground trong mạch trên. Vì vậy, chúng ta có thể sử dụngnodal analysisphương pháp. Điện áp nút V 1 và điện áp V Th của Thevenin được ghi nhãn trong hình trên. Ở đây, V 1 là điện áp từ nút 1 đối với mặt đất và V Th là điện áp trên nguồn dòng 4 A.
Các nodal equation tại nút 1 là
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} - 4 = 0$$
$$\Rightarrow \frac{2V_1 - 40 + V_1 - 40}{10} = 0$$
$$\Rightarrow 3V_1 - 80 = 0$$
$$\Rightarrow V_1 = \frac{80}{3}V$$
Điện áp trên nhánh nối tiếp với điện trở 10 Ω là
$$V_{10 \Omega} = (-4)(10) = -40V$$
Có hai mắt lưới trong đoạn mạch trên. CácKVL equation xung quanh lưới thứ hai là
$$V_1 - V_{10 \Omega} - V_{Th} = 0$$
Thay thế các giá trị của $V_1$ và $V_{10 \Omega}$ trong phương trình trên.
$$\frac{80}{3} - (-40) - V_{Th} = 0$$
$$V_{Th} = \frac{80 + 120}{3} = \frac{200}{3}V$$
Do đó, điện áp của Thevenin là $V_{Th} = \frac{200}{3}V$
Step 3 - Tính toán của Thevenin’s resistance RTh.
Ngắn mạch nguồn điện áp và để hở mạch nguồn dòng của đoạn mạch trên để tính điện trở R Th của Thevenin qua các đầu A & B.modified circuit diagram được hiển thị trong hình sau.
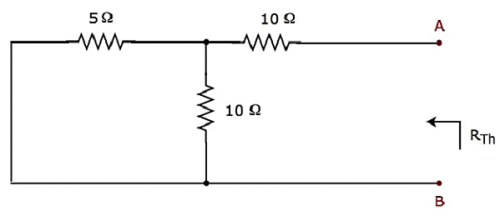
Sự kháng cự của Thevenin trên các thiết bị đầu cuối A & B sẽ là
$$R_{Th} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$
Do đó, sự phản kháng của Thevenin là $\mathbf {R_{Th} = \frac{40}{3} \Omega}$.
Step 4- Mạch tương đương của Thevenin được đặt ở bên trái của đầu cuối A & B trong mạch đã cho. Sơ đồ mạch này được hiển thị trong hình sau.

Dòng điện chạy qua điện trở 20 Ω có thể được tìm thấy bằng cách thay các giá trị của V Th , R Th và R vào phương trình sau.
$$l = \frac{V_{Th}}{R_{Th} + R}$$
$$l = \frac{\frac{200}{3}}{\frac{40}{3} + 20} = \frac{200}{100} = 2A$$
Do đó, cường độ dòng điện chạy qua điện trở 20 Ω là 2 A.
Phương pháp 2
Làm theo các bước sau để tìm mạch tương đương của Thevenin, khi sources of both independent type and dependent type đang có mặt.
Step 1 - Xem xét sơ đồ mạch điện bằng cách mở các đầu nối mà mạch tương đương của Thevenin sẽ được tìm thấy.
Step 2 - Tìm điện áp của Thevenin VTh qua các đầu cuối hở của đoạn mạch trên.
Step 3 - Tìm dòng ngắn mạch ISC bằng cách nối tắt hai cực đã mở của đoạn mạch trên.
Step 4 - Tìm sự kháng cự của Thevenin RTh bằng cách sử dụng công thức sau.
$$R_{Th} = \frac{V_{Th}}{I_{SC}}$$
Step 5 - Vẽ Thevenin’s equivalent circuitbằng cách mắc nối tiếp điện áp V Th của Thevenin với điện trở của Thevenin R Th .
Bây giờ, chúng ta có thể tìm thấy phản ứng trong một phần tử nằm ở phía bên phải của mạch tương đương của Thevenin.
Norton’s theoremtương tự như định lý Thevenin. Nó nói rằng bất kỳ mạng hoặc mạch tuyến tính hai đầu cuối nào cũng có thể được biểu diễn bằng một mạng hoặc mạch tương đương, bao gồm một nguồn dòng điện song song với một điện trở. Nó được biết đến nhưNorton’s equivalent circuit. A linear circuit may contain independent sources, dependent sources and resistors.
If a circuit has multiple independent sources, dependent sources, and resistors, then the response in an element can be easily found by replacing the entire network to the left of that element with a Norton’s equivalent circuit.
The response in an element can be the voltage across that element, current flowing through that element or power dissipated across that element.
This concept is illustrated in following figures.
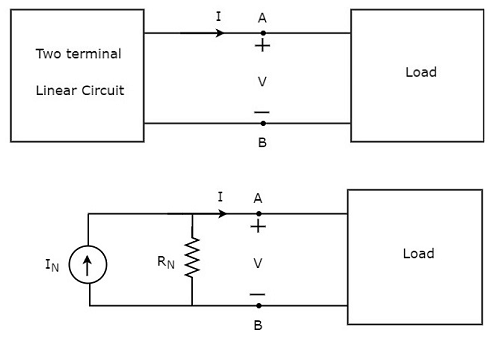
Norton’s equivalent circuit resembles a practical current source. Hence, it is having a current source in parallel with a resistor.
The current source present in the Norton’s equivalent circuit is called as Norton’s equivalent current or simply Norton’s current IN.
The resistor present in the Norton’s equivalent circuit is called as Norton’s equivalent resistor or simply Norton’s resistor RN.
Methods of Finding Norton’s Equivalent Circuit
There are three methods for finding a Norton’s equivalent circuit. Based on the type of sources that are present in the network, we can choose one of these three methods. Now, let us discuss these three methods one by one.
Method 1
Follow these steps in order to find the Norton’s equivalent circuit, when only the sources of independent type are present.
Step 1 − Consider the circuit diagram by opening the terminals with respect to which, the Norton’s equivalent circuit is to be found.
Step 2 − Find the Norton’s current IN by shorting the two opened terminals of the above circuit.
Step 3 − Find the Norton’s resistance RN across the open terminals of the circuit considered in Step1 by eliminating the independent sources present in it. Norton’s resistance RN will be same as that of Thevenin’s resistance RTh.
Step 4 − Draw the Norton’s equivalent circuit by connecting a Norton’s current IN in parallel with Norton’s resistance RN.
Now, we can find the response in an element that lies to the right side of Norton’s equivalent circuit.
Method 2
Follow these steps in order to find the Norton’s equivalent circuit, when the sources of both independent type and dependent type are present.
Step 1 − Consider the circuit diagram by opening the terminals with respect to which the Norton’s equivalent circuit is to be found.
Step 2 − Find the open circuit voltage VOC across the open terminals of the above circuit.
Step 3 − Find the Norton’s current IN by shorting the two opened terminals of the above circuit.
Step 4 − Find Norton’s resistance RN by using the following formula.
$$R_N = \frac{V_{OC}}{I_N}$$
Step 5 − Draw the Norton’s equivalent circuit by connecting a Norton’s current IN in parallel with Norton’s resistance RN.
Now, we can find the response in an element that lies to the right side of Norton’s equivalent circuit.
Method 3
This is an alternate method for finding a Norton’s equivalent circuit.
Step 1 − Find a Thevenin’s equivalent circuit between the desired two terminals. We know that it consists of a Thevenin’s voltage source, VTh and Thevenin’s resistor, RTh.
Step 2 − Apply source transformation technique to the above Thevenin’s equivalent circuit. We will get the Norton’s equivalent circuit. Here,
Norton’s current,
$$I_N = \frac{V_{Th}}{R_{Th}}$$
Norton’s resistance,
$$R_N = R_{Th}$$
This concept is illustrated in the following figure.
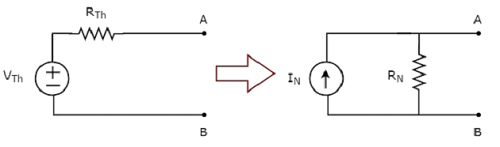
Now, we can find the response in an element by placing Norton’s equivalent circuit to the left of that element.
Note − Similarly, we can find the Thevenin’s equivalent circuit by finding a Norton’s equivalent circuit first and then apply source transformation technique to it. This concept is illustrated in the following figure.
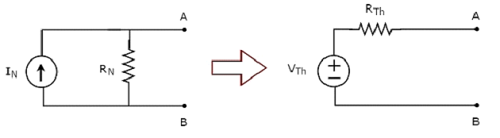
This is the Method 3 for finding a Thevenin’s equivalent circuit.
Example
Find the current flowing through 20 Ω resistor by first finding a Norton’s equivalent circuit to the left of terminals A and B.
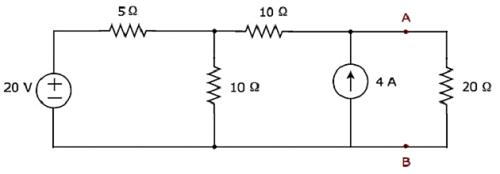
Let us solve this problem using Method 3.
Step 1 − In previous chapter, we calculated the Thevenin’s equivalent circuit to the left side of terminals A & B. We can use this circuit now. It is shown in the following figure.
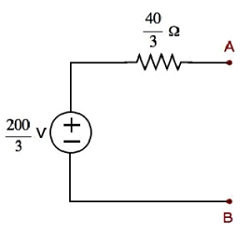
Here, Thevenin’s voltage, $V_{Th} = \frac{200}{3} V$ and Thevenin’s resistance, $R_{Th} = \frac{40}{3} \Omega$
Step 2 − Apply source transformation technique to the above Thevenin’s equivalent circuit. Substitute the values of VTh and RTh in the following formula of Norton’s current.
$$I_N = \frac{V_{Th}}{R_{Th}}$$
$$I_N = \frac{\frac{200}{3}}{\frac{40}{3}} = 5A$$
Therefore, Norton’s current IN is 5 A.
We know that Norton’s resistance, RN is same as that of Thevenin’s resistance RTh.
$$\mathbf {R_N = \frac{40}{3} \Omega}$$
The Norton’s equivalent circuit corresponding to the above Thevenin’s equivalent circuit is shown in the following figure.
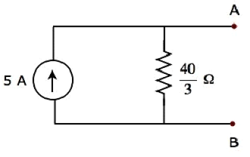
Now, place the Norton’s equivalent circuit to the left of the terminals A & B of the given circuit.
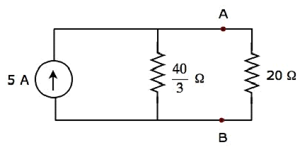
By using current division principle, the current flowing through the 20 Ω resistor will be
$$I_{20 \Omega} = 5 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup$$
$$I_{20 \Omega} = 5 \lgroup \frac{40}{100} \rgroup = 2A$$
Therefore, the current flowing through the 20 Ω resistor is 2 A.
The amount of power received by a load is an important parameter in electrical and electronic applications. In DC circuits, we can represent the load with a resistor having resistance of RL ohms. Similarly, in AC circuits, we can represent it with a complex load having an impedance of ZL ohms.
Maximum power transfer theorem states that the DC voltage source will deliver maximum power to the variable load resistor only when the load resistance is equal to the source resistance.
Similarly, Maximum power transfer theorem states that the AC voltage source will deliver maximum power to the variable complex load only when the load impedance is equal to the complex conjugate of source impedance.
In this chapter, let us discuss about the maximum power transfer theorem for DC circuits.
Proof of Maximum Power Transfer Theorem
Replace any two terminal linear network or circuit to the left side of variable load resistor having resistance of RL ohms with a Thevenin’s equivalent circuit. We know that Thevenin’s equivalent circuit resembles a practical voltage source.
This concept is illustrated in following figures.
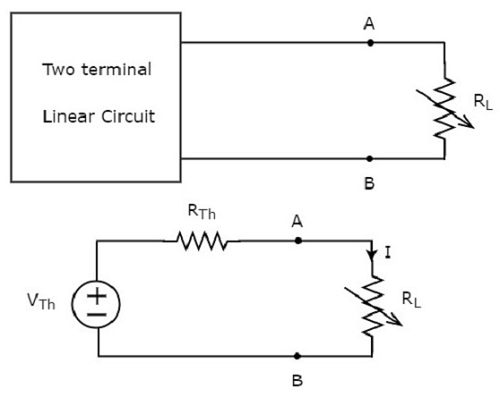
The amount of power dissipated across the load resistor is
$$P_L = I^2 R_L$$
Substitute $I = \frac{V_{Th}}{R_{Th} + R_L}$ in the above equation.
$$P_L = \lgroup \frac{V_{Th}}{(R_{Th} + R_L)} \rgroup ^2 R_L$$
$\Rightarrow P_L = {V_{Th}}^2 \lbrace \frac{R_L}{(R_{Th} + R_L)^2} \rbrace$ Equation 1
Condition for Maximum Power Transfer
For maximum or minimum, first derivative will be zero. So, differentiate Equation 1 with respect to RL and make it equal to zero.
$$\frac{dP_L}{dR_L} = {V_{Th}}^2 \lbrace \frac{(R_{Th} + R_L)^2 \times 1 - R_L \times 2(R_{Th} + R_L)}{(R_{Th} + R_L)^4} \rbrace = 0$$
$$\Rightarrow (R_{Th} + R_L)^2 -2R_L(R_{Th} + R_L) = 0$$
$$\Rightarrow (R_{Th} + R_L)(R_{Th} + R_L - 2R_L) = 0$$
$$\Rightarrow (R_{Th} - R_L) = 0$$
$$\Rightarrow R_{Th} = R_L\:or\:R_L = R_{Th}$$
Therefore, the condition for maximum power dissipation across the load is $R_L = R_{Th}$. That means, if the value of load resistance is equal to the value of source resistance i.e., Thevenin’s resistance, then the power dissipated across the load will be of maximum value.
The value of Maximum Power Transfer
Substitute $R_L = R_{Th}\:\&\:P_L = P_{L, Max}$ in Equation 1.
$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{(R_{Th} + R_{Th})^2} \rbrace$$
$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{4 {R_{Th}}^2} \rbrace$$
$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$
$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{L}}, \: since \: R_{L} = R_{Th}$$
Therefore, the maximum amount of power transferred to the load is
$$P_{L, Max} = \frac{{V_{Th}}^2}{4R_{L}} = \frac{{V_{Th}}^2}{4R_{Th}}$$
Efficiency of Maximum Power Transfer
We can calculate the efficiency of maximum power transfer, $\eta_{Max}$ using following formula.
$\eta_{Max} = \frac{P_{L, Max}}{P_S}$ Equation 2
Where,
$P_{L, Max}$ is the maximum amount of power transferred to the load.
$P_S$ is the amount of power generated by the source.
The amount of power generated by the source is
$$P_S = I^2 R_{Th} + I^2 R_L$$
$$\Rightarrow P_S = 2 I^2 R_{Th},\:since\:R_{L} = R_{Th}$$
Substitute $I = \frac{V_{Th}}{2 R_{Th}}$ in the above equation.
$$P_S = 2\lgroup \frac{V_{Th}}{2 R_{Th}} \rgroup ^2 R_{Th}$$
$$\Rightarrow P_S = 2\lgroup \frac{{V_{Th}}^2}{4 {R_{Th}}^2} \rgroup R_{Th}$$
$$\Rightarrow P_S = \frac{{V_{Th}}^2}{2 R_{Th}}$$
Substitute the values of $P_{L, Max}$ and $P_S$ in Equation 2.
$$\eta_{Max} = \frac{\lgroup \frac{{V_{Th}}^2}{4R_{Th}} \rgroup}{\lgroup \frac{{V_{Th}}^2}{2R_{Th}}\rgroup}$$
$$\Rightarrow \eta_{Max} = \frac{1}{2}$$
We can represent the efficiency of maximum power transfer in terms of percentage as follows −
$$\% \eta_{Max} = \eta_{Max} \times 100\%$$
$$\Rightarrow \% \eta_{Max} = \lgroup \frac{1}{2} \rgroup \times 100\%$$
$$\Rightarrow \% \eta_{Max} = 50\%$$
Therefore, the efficiency of maximum power transfer is 50 %.
Example
Find the maximum power that can be delivered to the load resistor RL of the circuit shown in the following figure.
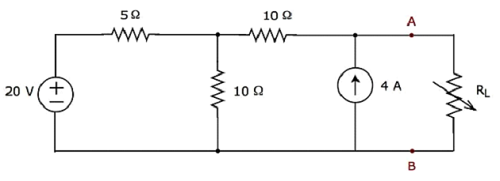
Step 1 − In Thevenin’s Theorem chapter, we calculated the Thevenin’s equivalent circuit to the left side of terminals A & B. We can use this circuit now. It is shown in the following figure.
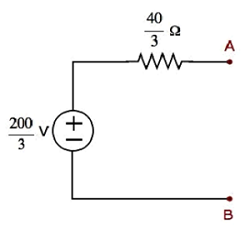
Here, Thevenin’s voltage $V_{Th} = \frac{200}{3}V$ and Thevenin’s resistance $R_{Th} = \frac{40}{3} \Omega$
Step 2 − Replace the part of the circuit, which is left side of terminals A & B of the given circuit with the above Thevenin’s equivalent circuit. The resultant circuit diagram is shown in the following figure.

Step 3- Chúng ta có thể tìm công suất lớn nhất sẽ cung cấp cho điện trở tải, R L bằng công thức sau.
$$P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$
Người thay thế $V_{Th} = \frac{200}{3}V$ và $R_{Th} = \frac{40}{3} \Omega$ trong công thức trên.
$$P_{L, Max} = \frac{\lgroup \frac{200}{3} \rgroup ^ 2}{4 \lgroup \frac{40}{3}\rgroup } $$
$$P_{L, Max} = \frac{250}{3} W$$
Do đó, maximum power sẽ được đưa đến điện trở tải RL của mạch đã cho là $\mathbf {\frac{250}{3}}$ W
Nếu đầu ra của mạch điện cho đầu vào thay đổi theo thời gian, thì nó được gọi là time response. Phản hồi thời gian bao gồm hai phần sau.
- Phản hồi thoáng qua
- Phản hồi ở trạng thái ổn định
Trong chương này, trước tiên chúng ta hãy thảo luận về hai phản ứng này và sau đó quan sát hai phản ứng này trong một mạch RL nối tiếp, khi nó được kích thích bởi nguồn điện áp một chiều.
Phản hồi thoáng qua
Sau khi đưa một đầu vào vào mạch điện, đầu ra cần một thời gian nhất định để đạt trạng thái ổn định. Vì vậy, đầu ra sẽ ở trạng thái tạm thời cho đến khi nó chuyển sang trạng thái ổn định. Do đó, phản ứng của mạch điện trong trạng thái quá độ được gọi làtransient response.
Phản hồi nhất thời sẽ bằng 0 đối với các giá trị lớn của 't'. Lý tưởng nhất, giá trị này của 't' phải là vô cùng. Nhưng, thực tếfive time constants là đủ.
Sự hiện diện hoặc Sự vắng mặt của Người chuyển tiếp
Quá độ xảy ra trong phản hồi do sudden changetrong các nguồn được áp dụng cho mạch điện và / hoặc do hoạt động đóng cắt. Có thể có hai hành động chuyển đổi. Đó là công tắc mở và công tắc đóng.
Các transient một phần sẽ not presenttrong phản ứng của mạch điện hoặc mạng, nếu nó chỉ chứa điện trở. Bởi vìresistor có khả năng điều chỉnh bất kỳ lượng điện áp và dòng điện nào.
Các transient part occurs trong phản ứng của mạch điện hoặc mạng do sự hiện diện của các phần tử tích trữ năng lượng như inductor and capacitor. Bởi vì chúng không thể thay đổi năng lượng được lưu trữ trong các nguyên tố đó ngay lập tức.
Hành vi cuộn cảm
Giả sử hành động chuyển đổi diễn ra tại t = 0.Inductor currentkhông thay đổi ngay lập tức, khi hành động chuyển đổi diễn ra. Điều đó có nghĩa là, giá trị của dòng điện dẫn ngay sau hành động chuyển mạch sẽ giống như giá trị của ngay trước hành động chuyển mạch.
Về mặt toán học, nó có thể được biểu diễn dưới dạng
$$i_L (0^+) = i_L (0^-)$$
Hành vi của tụ điện
Các capacitor voltagekhông thay đổi tức thời tương tự như dòng điện dẫn, khi hành động chuyển mạch diễn ra. Điều đó có nghĩa là, giá trị của điện áp tụ điện ngay sau hành động chuyển mạch sẽ giống như giá trị của ngay trước khi hành động chuyển mạch.
Về mặt toán học, nó có thể được biểu diễn dưới dạng
$$v_c (0^+) = v_c (0^-)$$
Phản hồi ở trạng thái ổn định
Phần phản hồi thời gian vẫn còn ngay cả sau khi phản hồi thoáng qua đã trở thành giá trị 0 đối với các giá trị lớn của 't' được gọi là steady state response. Điều này có nghĩa là, sẽ không có bất kỳ phần nào nhất thời trong phản hồi ở trạng thái ổn định.
Hành vi cuộn cảm
Nếu nguồn độc lập được nối với mạch điện hoặc mạng điện có một hoặc nhiều cuộn cảm và điện trở (tùy chọn) trong một thời gian dài, thì mạch điện hoặc mạng điện đó được cho là ở trạng thái ổn định. Do đó, năng lượng tích trữ trong (các) cuộn cảm của mạch điện đó là cực đại và không đổi.
Về mặt toán học, nó có thể được biểu diễn dưới dạng
$W_L = \frac{L {i_L}^2}{2} = $ Tối đa & không đổi
$\Rightarrow i_L = $ Tối đa & không đổi
Do đó, cuộn cảm hoạt động như một constant current source ở trạng thái ổn định.
Điện áp trên cuộn cảm sẽ là
$$V_L = L \frac{di_{L}}{dt} = 0V$$
Vì vậy, cuộn cảm hoạt động như một short circuit ở trạng thái ổn định.
Hành vi của tụ điện
Nếu nguồn độc lập được nối với mạch điện hoặc mạng điện có một hoặc nhiều tụ điện và điện trở (tùy chọn) trong thời gian dài, thì mạch điện hoặc mạng điện đó được cho là ở trạng thái ổn định. Do đó, năng lượng tích trữ trong (các) tụ điện của mạch điện đó là cực đại và không đổi.
Về mặt toán học, nó có thể được biểu diễn dưới dạng
$W_c = \frac{C{v_c}^2}{2} = $ Tối đa & không đổi
$\Rightarrow v_c = $Tối đa & không đổi
Do đó, tụ điện hoạt động như một constant voltage source ở trạng thái ổn định.
Dòng điện chạy qua tụ điện sẽ là
$$i_c = C\frac{dv_c}{dt} = 0A$$
Vì vậy, tụ điện hoạt động như một open circuit ở trạng thái ổn định.
Tìm phản hồi của mạch RL loạt
Hãy xem xét những điều sau series RL circuit biểu đồ.
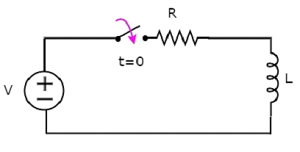
Trong mạch trên, switch đã được giữ openđến t = 0 và đóng ở t = 0. Vậy nguồn điện một chiều có V vôn chưa mắc vào đoạn mạch RL nối tiếp tính đến thời điểm này. Do đó, cóno initial current chảy qua cuộn cảm.
Sơ đồ mạch, khi switch trong closed vị trí được hiển thị trong hình sau.
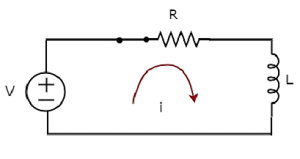
Bây giờ, hiện tại i chảy trong toàn bộ mạch, vì nguồn điện áp một chiều có V vôn được mắc vào mạch RL nối tiếp.
Bây giờ, áp dụng KVL xung quanh vòng lặp.
$$V = Ri + L \frac{di}{dt}$$
$\frac{di}{dt} + \lgroup \frac{R}{L} \rgroup i = \frac{V}{L}$Equation 1
Phương trình trên là một phương trình vi phân bậc nhất và nó có dạng
$\frac{dy}{dt} + Py = Q$Equation 2
Bởi comparing Phương trình 1 và phương trình 2, chúng ta sẽ nhận được các quan hệ sau.
$$x = t$$
$$y = i$$
$$P = \frac{R}{L}$$
$$Q = \frac{V}{L}$$
Các solution của phương trình 2 sẽ là
$ye^{\int p dx} = \int Q e^{\int p dx} dx + k$Equation 3
Ở đâu, k là hằng số.
Thay thế các giá trị của x, y, P & Q trong Công thức 3.
$ie^{\int {\lgroup \frac{R}{L} \rgroup}dt} = \int (\frac{V}{L}) \lgroup e^{\int {\lgroup \frac{R}{L} \rgroup}dt} \rgroup dt + k$
$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \int e^{\lgroup \frac{R}{L} \rgroup t} dt + k$
$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \lbrace \frac{e^{\lgroup \frac{R}{L} \rgroup}t}{\frac{R}{L}} \rbrace + k$
$\Rightarrow i = \frac{V}{R} + k e^{-\lgroup \frac{R}{L} \rgroup}t$Equation 4
Ta biết rằng trong mạch không có dòng điện ban đầu. Do đó, thay thế, t = 0 và = 0 trong phương trình 4 để tìm giá trị của hằng số k.
$$0 = \frac{V}{R} + ke^{-\lgroup \frac{R}{L} \rgroup(0)}$$
$$0 = \frac{V}{R} + k(1)$$
$$k = - \frac{V}{R}$$
Thay thế, giá trị của k trong phương trình 4.
$$i = \frac{V}{R} + \lgroup - \frac{V}{R} \rgroup e^{-\lgroup \frac{R}{L} \rgroup t}$$
$$i = \frac{V}{R} - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$$
Do đó, current chảy qua mạch là
$i = - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t} + \frac{V}{R}$Equation 5
Vậy phản ứng của đoạn mạch RL nối tiếp khi được kích thích bằng nguồn điện áp một chiều có hai số hạng sau.
Nhiệm kỳ đầu tiên $-\frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$ tương ứng với transient response.
Nhiệm kỳ thứ hai $\frac{V}{R}$ tương ứng với steady state response. Hai phản ứng này được hiển thị trong hình sau.
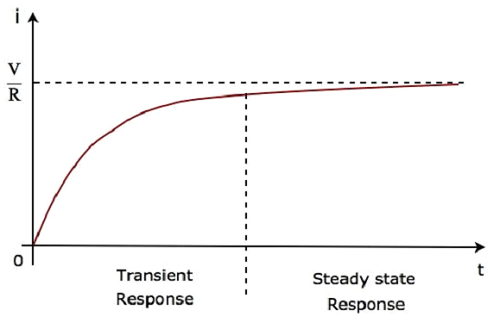
Chúng ta có thể viết lại phương trình 5 như sau:
$i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{R}{L} \rgroup t} \rgroup$
$\Rightarrow i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{t}{\tau} \rgroup} \rgroup$Equation 6
Ở đâu, τ là time constant và giá trị của nó bằng $\frac{L}{R}$.
Cả phương trình 5 và phương trình 6 đều giống nhau. Nhưng, chúng ta có thể dễ dàng hiểu dạng sóng trên của dòng điện chạy qua mạch từ phương trình 6 bằng cách thay thế một vài giá trị củat như 0, τ, 2τ, 5τ, v.v.
Trong dạng sóng trên của dòng điện chạy qua mạch, phản ứng thoáng qua sẽ có tới năm hằng số thời gian từ 0, trong khi phản ứng trạng thái ổn định sẽ có từ năm hằng số thời gian trở đi.
Trong chương trước, chúng ta đã thảo luận về đáp ứng quá độ và đáp ứng trạng thái ổn định của mạch DC. Trong chương này, chúng ta hãy thảo luận vềresponse of AC circuit. Các khái niệm về cả phản ứng nhất thời và phản ứng trạng thái ổn định, mà chúng ta đã thảo luận trong chương trước, cũng sẽ hữu ích ở đây.
Tìm phản hồi của mạch RL loạt
Hãy xem xét những điều sau series RL circuit biểu đồ.

Trong mạch trên, switch đã được giữ openđến t = 0 và nó được đóng ở t = 0 . Vậy nguồn điện áp xoay chiều có hiệu điện thế đỉnh là V m vôn không mắc vào đoạn mạch RL nối tiếp tính đến thời điểm này. Do đó, cóno initial current chảy qua cuộn cảm.
Sơ đồ mạch, khi switch trong closed vị trí, được hiển thị trong hình sau.
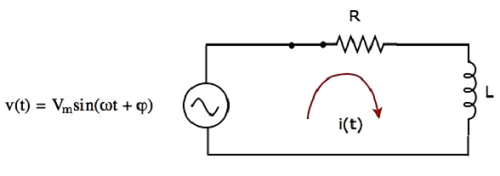
Bây giờ, dòng điện i (t) chạy trong toàn mạch, vì nguồn điện áp xoay chiều có điện áp cực đại là V m vôn được nối với mạch RL nối tiếp.
Ta biết rằng dòng điện i (t) chạy qua đoạn mạch trên sẽ có hai số hạng, một số hạng biểu thị phần quá độ và số hạng còn lại biểu thị trạng thái dừng.
Về mặt toán học, nó có thể được biểu diễn dưới dạng
$i(t) = i_{Tr}(t) + i_{ss}(t)$Equation 1
Ở đâu,
$i_{Tr}(t)$ là phản ứng quá độ của dòng điện chạy qua đoạn mạch.
$i_{ss}(t)$ là phản ứng ở trạng thái dừng của dòng điện chạy qua mạch.
Trong chương trước, chúng ta đã nhận được phản ứng quá độ của dòng điện chạy qua đoạn mạch RL nối tiếp. Nó ở dạng$Ke^{-\lgroup \frac{t}{\tau} \rgroup}$.
Người thay thế $i_{Tr}(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup}$ trong phương trình 1.
$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + i_{ss}(t)$Equation 2
Tính toán trạng thái ổn định hiện tại
Nếu tín hiệu hình sin được áp dụng làm đầu vào cho mạch điện tuyến tính, thì nó tạo ra đầu ra trạng thái ổn định, cũng là sinusoidal signal. Cả tín hiệu hình sin đầu vào và đầu ra sẽ có cùng tần số, nhưng biên độ và góc pha khác nhau.
Chúng ta có thể tính đáp ứng trạng thái ổn định của một mạch điện, khi nó được kích thích bởi nguồn điện áp hình sin sử dụng Laplace Transform approach.
Sơ đồ mạch miền s, khi switch trong closed vị trí, được hiển thị trong hình sau.
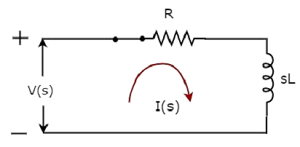
Trong mạch trên, tất cả các đại lượng và thông số được biểu diễn bằng s-domain. Đây là các phép biến đổi Laplace của các đại lượng và tham số trong miền thời gian.
Các Transfer function của đoạn mạch trên là
$$H(s) = \frac{I(s)}{V(s)}$$
$$\Rightarrow H(s) = \frac{1}{Z(s)}$$
$$\Rightarrow H(s) = \frac{1}{R + sL}$$
Người thay thế $s = j \omega$ trong phương trình trên.
$$H(j \omega) = \frac{1}{R + j \omega L}$$
Magnitude of $\mathbf{\mathit{H(j \omega)}}$ Là
$$|H(j \omega)| = \frac{1}{\sqrt{R^2 + {\omega}^2}L^2}$$
Phase angle of $\mathbf{\mathit{H(j \omega)}}$ Là
$$\angle H(j \omega) = -tan^{-1} \lgroup \frac{\omega L}{R} \rgroup$$
Chúng tôi sẽ nhận được steady state current $i_{ss}(t)$ bằng cách thực hiện hai bước sau:
Nhân điện áp đỉnh của điện áp hình sin đầu vào và độ lớn của $H(j \omega)$.
Thêm các góc pha của điện áp hình sin đầu vào và $H(j \omega)$.
Các steady state current $i_{ss}(t)$ sẽ là
$$i_{ss}(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Thay thế giá trị của $i_{ss}(t)$ trong phương trình 2.
$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 3
Ta biết rằng trong mạch không có dòng điện ban đầu. Do đó, thay t = 0 & i (t) = 0 trong Công thức 3 để tìm giá trị của hằng số, K.
$$0 = Ke^{-\lgroup \frac{0}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega (0) + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
$$\Rightarrow 0 = K + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
$$\Rightarrow K = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Thay giá trị của K trong Phương trình 3.
$i(t) = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup e^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 4
Công thức 4 biểu diễn cường độ dòng điện chạy qua đoạn mạch RL nối tiếp, khi nó được kích thích bằng nguồn điện áp hình sin. Nó có hai điều khoản. Số hạng đầu tiên và số hạng thứ hai đại diện cho phản ứng nhất thời và phản ứng trạng thái ổn định của dòng điện tương ứng.
Chúng ta có thể neglect the first termcủa phương trình 4 vì giá trị của nó sẽ nhỏ hơn rất nhiều. Vì vậy, kết quả của dòng điện chạy qua mạch sẽ là
$$i(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Nó chỉ chứa steady state term. Do đó, chúng ta chỉ có thể tìm thấy phản ứng trạng thái ổn định của mạch xoay chiều và bỏ qua phản ứng thoáng qua của nó.
Resonancexảy ra trong mạch điện do sự hiện diện của các phần tử lưu trữ năng lượng như cuộn cảm và tụ điện. Đó là khái niệm cơ bản dựa trên đó, máy thu thanh và máy thu TV được thiết kế theo cách mà chúng chỉ có thể chọn tần số đài mong muốn.
Có two typescộng hưởng, cụ thể là cộng hưởng nối tiếp và cộng hưởng song song. Chúng được phân loại dựa trên các phần tử mạng được kết nối nối tiếp hoặc song song. Trong chương này, chúng ta hãy thảo luận về cộng hưởng chuỗi.
Sơ đồ mạch cộng hưởng nối tiếp
Nếu hiện tượng cộng hưởng xảy ra trong đoạn mạch RLC nối tiếp thì gọi là Series Resonance. Hãy xem xét những điều sauseries RLC circuit, được đại diện trong miền phasor.
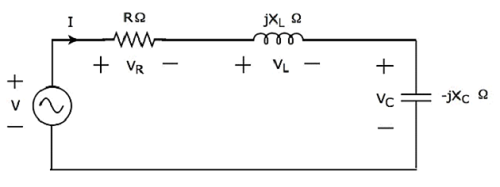
Ở đây, các phần tử thụ động như điện trở, cuộn cảm và tụ điện được mắc nối tiếp. Toàn bộ sự kết hợp này nằm trongseries với nguồn điện áp hình sin đầu vào.
Ứng dụng KVL xung quanh vòng lặp.
$$V - V_R - V_L - V_C = 0$$
$$\Rightarrow V - IR - I(j X_L) - I(-j X_C) = 0$$
$$\Rightarrow V = IR + I(j X_L) + I(-j X_C)$$
$\Rightarrow V = I[R + j(X_L - X_C)]$Equation 1
Phương trình trên có dạng V = IZ.
Do đó, impedance Z của mạch RLC nối tiếp sẽ là
$$Z = R + j(X_L - X_C)$$
Thông số & Đại lượng điện tại cộng hưởng
Bây giờ, chúng ta hãy suy ra các giá trị của các thông số và các đại lượng điện khi cộng hưởng của đoạn mạch RLC nối tiếp lần lượt.
Tần số cộng hưởng
Tần số tại đó xảy ra cộng hưởng được gọi là resonant frequency fr. Trong đoạn mạch RLC nối tiếp xảy ra cộng hưởng khi số hạng ảo của tổng trở Z bằng không, nghĩa là giá trị của$X_L - X_C$ nên bằng không.
$$\Rightarrow X_L = X_C$$
Người thay thế $X_L = 2 \pi f L$ và $X_C = \frac{1}{2 \pi f C}$ trong phương trình trên.
$$2 \pi f L = \frac{1}{2 \pi f C}$$
$$\Rightarrow f^2 = \frac{1}{(2 \pi)^2 L C}$$
$$\Rightarrow f = \frac{1}{(2 \pi) \sqrt{LC}}$$
Do đó, resonant frequency fr của đoạn mạch RLC nối tiếp là
$$f_r = \frac{1}{(2 \pi) \sqrt{LC}}$$
Ở đâu, L là độ tự cảm của một cuộn cảm và C là điện dung của tụ điện.
Các resonant frequency fr của đoạn mạch RLC nối tiếp chỉ phụ thuộc vào độ tự cảm L và điện dung C. Nhưng, nó độc lập với sự phản khángR.
Trở kháng
Chúng tôi có impedance Z của đoạn mạch RLC nối tiếp là
$$Z = R + j(X_L - X_C)$$
Người thay thế $X_L = X_C$ trong phương trình trên.
$$Z = R + j(X_C - X_C)$$
$$\Rightarrow Z = R + j(0)$$
$$\Rightarrow Z = R$$
Khi cộng hưởng, impedance Z của đoạn mạch RLC nối tiếp bằng giá trị của cảm kháng R, I E, Z = R.
Dòng điện chạy qua mạch
Người thay thế $X_L - X_C = 0$ trong phương trình 1.
$$V = I[R + j(0)]$$
$$\Rightarrow V = IR$$
$$\Rightarrow I = \frac{V}{R}$$
Vì thế, current chạy qua đoạn mạch RLC nối tiếp lúc cộng hưởng là $\mathbf{\mathit{I = \frac{V}{R}}}$.
Khi xảy ra cộng hưởng, tổng trở của đoạn mạch RLC nối tiếp đạt giá trị cực tiểu. Vì thếmaximum current chảy qua mạch này lúc cộng hưởng.
Điện áp trên điện trở
Điện áp trên điện trở là
$$V_R = IR$$
Thay thế giá trị của I trong phương trình trên.
$$V_R = \lgroup \frac{V}{R} \rgroup R$$
$$\Rightarrow V_R = V$$
Do đó, voltage across resistor lúc cộng hưởng là VR = V.
Điện áp trên cuộn cảm
Điện áp trên cuộn cảm là
$$V_L = I(jX_L)$$
Thay thế giá trị của I trong phương trình trên.
$$V_L = \lgroup \frac{V}{R} \rgroup (jX_L)$$
$$\Rightarrow V_L = j \lgroup \frac{X_L}{R} \rgroup V$$
$$\Rightarrow V_L = j QV$$
Do đó, voltage across inductor lúc cộng hưởng là $V_L = j QV$.
Nên magnitude của điện áp trên cuộn cảm khi cộng hưởng sẽ là
$$|V_L| = QV$$
Ở đâu Q là Quality factor và giá trị của nó bằng $\frac{X_L}{R}$
Điện áp trên tụ điện
Hiệu điện thế trên tụ điện là
$$V_C = I(-j X_C)$$
Thay giá trị của I vào phương trình trên.
$$V_C = \lgroup \frac{V}{R} \rgroup (-j X_C)$$
$$\Rightarrow V_C = -j \lgroup \frac{X_C}{R} \rgroup V$$
$$\Rightarrow V_C = -jQV$$
Do đó, voltage across capacitor lúc cộng hưởng là $\mathbf{\mathit{V_C = -jQV}}$.
Nên magnitude của điện áp trên tụ điện lúc cộng hưởng sẽ là
$$|V_C| = QV$$
Ở đâu Q là Quality factor và giá trị của nó bằng $\frac{X_{C}}{R}$
Note - Đoạn mạch RLC nối tiếp cộng hưởng được gọi là voltage magnificationmạch, vì độ lớn của điện áp trên cuộn cảm và tụ điện bằng Q nhân với điện áp hình sin V đầu vào .
Trong chương trước, chúng ta đã thảo luận về tầm quan trọng của cộng hưởng chuỗi. Bây giờ, chúng ta hãy thảo luận về cộng hưởng song song trong mạch RLC.
Sơ đồ mạch cộng hưởng song song
Nếu xảy ra hiện tượng cộng hưởng trong đoạn mạch RLC song song thì gọi là Parallel Resonance. Hãy xem xét những điều sauparallel RLC circuit, được đại diện trong miền phasor.
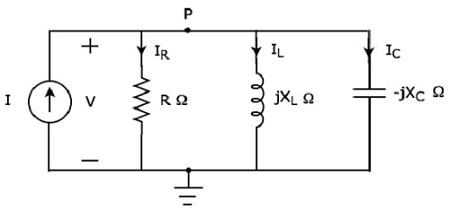
Ở đây, các phần tử thụ động như điện trở, cuộn cảm và tụ điện được kết nối song song. Toàn bộ sự kết hợp này nằm trongparallel với nguồn dòng hình sin đầu vào.
Viết nodal equation tại nút P.
$$- I + I_R + I_L + I_C = 0$$
$$\Rightarrow - I + \frac{V}{R} + \frac{V}{j X_L} + \frac{V}{-j X_C} = 0$$
$$\Rightarrow I = \frac{V}{R} - \frac{jV}{X_L} + \frac{jV}{X_C}$$
$\Rightarrow I = V[\frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup]$Equation 1
Phương trình trên có dạng I = VY.
Do đó, admittance Y của đoạn mạch RLC song song sẽ là
$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$
Thông số & Đại lượng điện tại cộng hưởng
Bây giờ, chúng ta hãy suy ra giá trị của các thông số và các đại lượng điện khi cộng hưởng của đoạn mạch RLC song song lần lượt.
Tần số cộng hưởng
Chúng tôi biết rằng resonant frequency, frlà tần số tại đó xảy ra hiện tượng cộng hưởng. Trong đoạn mạch RLC song song xảy ra cộng hưởng, khi số hạng ảo của thừa nhận Y bằng không. tức là, giá trị của$\frac{1}{X_C} - \frac{1}{X_L}$ phải bằng 0
$$\Rightarrow \frac{1}{X_C} = \frac{1}{X_L}$$
$$\Rightarrow X_L = X_C$$
Điều kiện cộng hưởng trên giống như điều kiện của đoạn mạch RLC nối tiếp. Nênresonant frequency, fr sẽ giống nhau trong đoạn mạch RLC nối tiếp và đoạn mạch RLC song song.
Do đó, resonant frequency, fr của đoạn mạch RLC song song là
$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$
Ở đâu,
- L là độ tự cảm của cuộn cảm.
- C là điện dung của tụ điện.
Các resonant frequency, fr của đoạn mạch RLC song song chỉ phụ thuộc vào độ tự cảm L và điện dung C. Nhưng, nó độc lập với sự phản khángR.
Chuyển tiền
Chúng tôi có admittance Y của đoạn mạch RLC song song là
$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$
Thay thế, $X_L = X_C$ trong phương trình trên.
$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_C} \rgroup$$
$$\Rightarrow Y = \frac{1}{R} + j(0)$$
$$\Rightarrow Y = \frac{1}{R}$$
Khi cộng hưởng, admittance, Y của đoạn mạch RLC song song bằng nghịch đảo của cảm kháng R. tức là $\mathbf{\mathit{Y = \frac{1}{R}}}$
Điện áp trên mỗi phần tử
Thay thế, $\frac{1}{X_C} - \frac{1}{X_L} = 0$ trong phương trình 1
$$I = V [\frac{1}{R} + j(0)]$$
$$\Rightarrow I = \frac{V}{R}$$
$$\Rightarrow V = IR$$
Do đó, voltage trên tất cả các phần tử của đoạn mạch RLC song song lúc cộng hưởng là V = IR.
Lúc xảy ra hiện tượng cộng hưởng, cảm ứng của đoạn mạch RLC song song đạt giá trị cực tiểu. Vì thế,maximum voltage hiện diện trên mỗi phần tử của mạch này khi cộng hưởng.
Dòng điện chạy qua điện trở
Cường độ dòng điện chạy qua điện trở là
$$I_R = \frac{V}{R}$$
Thay thế giá trị của V trong phương trình trên.
$$I_R = \frac{IR}{R}$$
$$\Rightarrow I_R = I$$
Do đó, current flowing through resistor lúc cộng hưởng là $\mathbf{\mathit{I_R = I}}$.
Dòng điện chạy qua cuộn cảm
Dòng điện chạy qua cuộn cảm là
$$I_L = \frac{V}{j X_L}$$
Thay thế giá trị của V trong phương trình trên.
$$I_L = \frac{IR}{j X_L}$$
$$\Rightarrow I_L = -j \lgroup \frac{R}{X_L} \rgroup I$$
$$\Rightarrow I_L = -jQI$$
Do đó, current flowing through inductor lúc cộng hưởng là $I_L = -jQI$.
Nên magnitude dòng điện chạy qua cuộn cảm lúc cộng hưởng sẽ
$$|I_L| = QI$$
Ở đâu, Q là Quality factor và giá trị của nó bằng $\frac{R}{X_L}$
Dòng điện chạy qua tụ điện
Cường độ dòng điện chạy qua tụ điện là
$$I_C = \frac{V}{-j X_C}$$
Thay thế giá trị của V trong phương trình trên.
$$I_C = \frac{IR}{-j X_C}$$
$$\Rightarrow I_C = j \lgroup \frac{R}{X_C} \rgroup I$$
$$\Rightarrow I_C = jQI$$
Do đó, current flowing through capacitor lúc cộng hưởng là $I_C = jQI$
Nên magnitude dòng điện chạy qua tụ điện lúc cộng hưởng sẽ
$$|I_C| = QI$$
Ở đâu, Q là Quality factor và giá trị của nó bằng $\frac{R}{X_C}$
Note - Đoạn mạch RLC cộng hưởng song song được gọi là current magnificationmạch điện. Vì, cường độ dòng điện chạy qua cuộn cảm và tụ điện bằng Q lần dòng điện hình sin I vào .
Một mạch điện được cho là coupled circuit, khi tồn tại cảm kháng lẫn nhau giữa các cuộn dây (hoặc cuộn cảm) có trong đoạn mạch đó. Cuộn dây không là gì ngoài sự kết hợp nối tiếp của điện trở và cuộn cảm. Trong trường hợp không có điện trở, cuộn dây trở thành cuộn cảm. Đôi khi, thuật ngữ cuộn dây và cuộn cảm được sử dụng thay thế cho nhau.
Trong chương này, đầu tiên chúng ta hãy thảo luận về quy ước dấu chấm và sau đó sẽ thảo luận về phân loại ghép nối.
Công ước chấm
Quy ước chấm là một kỹ thuật, cung cấp các chi tiết về cực tính của điện áp tại đầu cuối có chấm. Thông tin này rất hữu ích khi viết phương trình KVL.
Nếu dòng điện đi vào đầu cuối có chấm của một cuộn dây (hoặc cuộn cảm), thì nó tạo ra điện áp ở cuộn dây khác (hoặc cuộn cảm), đang có positive polarity tại thiết bị đầu cuối có dấu chấm.
Nếu dòng điện rời khỏi đầu nối có chấm của một cuộn dây (hoặc cuộn cảm), thì nó tạo ra điện áp ở cuộn dây khác (hoặc cuộn cảm), đang có negative polarity tại thiết bị đầu cuối có dấu chấm.
Phân loại khớp nối
Chúng tôi có thể phân loại coupling thành hai loại sau.
- Khớp nối điện
- Khớp nối từ tính
Bây giờ, chúng ta hãy thảo luận về từng loại khớp nối một.
Khớp nối điện
Sự ghép nối điện xảy ra, khi tồn tại một physical connectiongiữa hai cuộn dây (hoặc cuộn cảm). Khớp nối này có thể là loại hỗ trợ hoặc loại đối lập. Nó dựa trên việc dòng điện đi vào đầu cuối có chấm hay rời khỏi đầu cuối có chấm.
Khớp nối kiểu trợ giúp
Xét mạch điện sau đây có hai cuộn cảm mắc nối tiếp với nhau series.
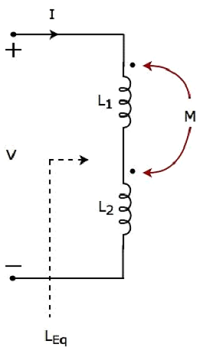
Vì hai cuộn cảm mắc nối tiếp nên same current Ichạy qua hai cuộn cảm có độ tự cảm L 1 và L 2 .
Trong trường hợp này, dòng điện, tôi nhập vào đầu cuối có dấu chấm của mỗi cuộn cảm. Do đó, điện áp cảm ứng trong mỗi cuộn cảm sẽ cópositive polarity ở đầu cuối có chấm do dòng điện chạy trong cuộn dây khác.
Ứng dụng KVL xung quanh vòng dây của mạch điện hoặc mạng điện trên.
$$V - L_1 \frac{dI}{dt} - M \frac{dI}{dt} - L_2 \frac{dI}{dt} - M \frac{dI}{dt} = 0$$
$$V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} + 2M \frac{dI}{dt}$$
$$V = (L_1 + L_2 + 2M)\frac{dI}{dt}$$
Phương trình trên có dạng $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$
Do đó, equivalent inductance tổng hợp nối tiếp của cuộn cảm được biểu diễn trong hình trên là
$$L_{Eq} = L_1 + L_2 + 2M$$
Trong trường hợp này, độ tự cảm tương đương đã được tăng thêm 2M. Do đó, mạch điện trên là một ví dụ vềelectrical khớp nối là của aiding kiểu.
Khớp nối kiểu đối lập
Xét mạch điện sau đây có hai cuộn cảm mắc nối tiếp với nhau series.
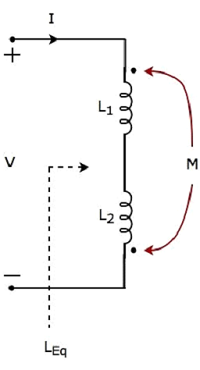
Trong đoạn mạch trên, dòng điện I đi vào đầu cuối có chấm của cuộn cảm có độ tự cảm là L1. Do đó, nó tạo ra một điện áp trong cuộn cảm khác có độ tự cảm làL2. Vì thế,positive polarity của điện áp cảm ứng hiện diện ở đầu nối chấm của cuộn cảm này.
Trong đoạn mạch trên, dòng điện I rời khỏi đầu cuối chấm của cuộn cảm có độ tự cảm L2. Do đó, nó tạo ra một điện áp trong cuộn cảm khác có độ tự cảm làL1. Vì thế,negative polarity của điện áp cảm ứng hiện diện ở đầu nối chấm của cuộn cảm này.
Ứng dụng KVL xung quanh vòng dây của mạch điện hoặc mạng điện trên.
$$V - L_1 \frac{dI}{dt} + M \frac{dI}{dt} - L_2 \frac{dI}{dt} + M \frac{dI}{dt} = 0$$
$$\Rightarrow V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} - 2M \frac{dI}{dt}$$
$$\Rightarrow V = (L_1 + L_2 - 2M)\frac{dI}{dt}$$
Phương trình trên có dạng $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$
Do đó, equivalent inductance tổng hợp nối tiếp của cuộn cảm được biểu diễn trong hình trên là
$$L_{Eq} = L_1 + L_2 - 2M$$
Trong trường hợp này, độ tự cảm tương đương đã giảm đi 2M. Do đó, mạch điện trên là một ví dụ vềelectrical khớp nối là của opposing kiểu.
Khớp nối từ tính
Khớp nối từ xảy ra, khi có no physical connectiongiữa hai cuộn dây (hoặc cuộn cảm). Khớp nối này có thể là loại hỗ trợ hoặc loại đối lập. Nó dựa trên việc dòng điện đi vào đầu cuối có chấm hay rời khỏi đầu cuối có chấm.
Khớp nối kiểu trợ giúp
Xem xét điện tương đương sau circuit of transformer. Nó có hai cuộn dây và chúng được gọi là cuộn dây chính và cuộn thứ cấp.
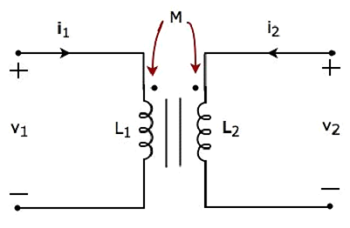
Cường độ dòng điện chạy qua cuộn sơ cấp và cuộn thứ cấp lần lượt là i 1 và i 2 . Trong trường hợp này, các dòng điện nàyentertại đầu cuối có chấm của cuộn dây tương ứng. Do đó, điện áp cảm ứng trong mỗi cuộn dây sẽ có cực tính dương ở đầu nối chấm do dòng điện chạy trong cuộn dây khác.
Ứng dụng KVL xung quanh cuộn sơ cấp.
$$v_1 - L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt} = 0$$
$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt}$Equation 1
Ứng dụng KVL xung quanh cuộn thứ cấp.
$$v_2 - L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt} = 0$$
$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt}$Equation 2
Trong phương trình 1 và phương trình 2, điện áp tự ngẫu và điện áp cảm ứng biến đổi có cùng cực. Do đó, mạch biến áp trên là một ví dụ vềmagnetic coupling, là của aiding kiểu.
Khớp nối của loại đối lập
Xem xét điện tương đương sau circuit of transformer.

Cường độ dòng điện chạy qua cuộn sơ cấp và cuộn thứ cấp lần lượt là i 1 và i 2 . Trong trường hợp này, dòng điện, i 1 đi vào đầu nối chấm của cuộn sơ cấp. Do đó, nó tạo ra một điện áp trong cuộn thứ cấp. Vì thế,positive polarity của điện áp cảm ứng có ở đầu nối chấm của cuộn thứ cấp này.
Trong đoạn mạch trên, dòng điện i 2 ra khỏi đầu nối tiếp nhau của cuộn thứ cấp. Do đó, nó tạo ra một điện áp trong cuộn sơ cấp. Vì thế,negative polarity của điện áp cảm ứng hiện diện ở đầu nối chấm của cuộn sơ cấp này.
Ứng dụng KVL xung quanh cuộn sơ cấp.
$$v_1 - L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt} = 0$$
$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt}$Equation 3
Ứng dụng KVL xung quanh cuộn thứ cấp.
$$v_2 - L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt} = 0$$
$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt}$Equation 4
Trong phương trình 3 và phương trình 4, điện áp tự ngẫu và điện áp cảm ứng biến đổi có cực tính ngược nhau. Do đó, mạch biến áp trên là một ví dụ vềmagnetic coupling, là của opposing kiểu.
Nói chung, có thể dễ dàng phân tích bất kỳ mạng điện nào, nếu nó được biểu diễn bằng một mô hình tương đương, cho mối quan hệ giữa các biến đầu vào và đầu ra. Đối với điều này, chúng ta có thể sử dụngtwo port networkcác đại diện. Như tên cho thấy, hai mạng cổng chứa hai cổng. Trong đó, một cổng được sử dụng làm cổng đầu vào và cổng còn lại được sử dụng làm cổng đầu ra. Cổng đầu tiên và cổng thứ hai được gọi tương ứng là cổng1 và cổng2.
One port networklà một mạng điện hai đầu cuối, trong đó, dòng điện đi qua một đầu cuối và đi qua một đầu cuối khác. Điện trở, cuộn cảm và tụ điện là các ví dụ của mạng một cổng vì mỗi mạng có hai đầu cuối. Biểu diễn mạng một cổng được thể hiện trong hình sau.
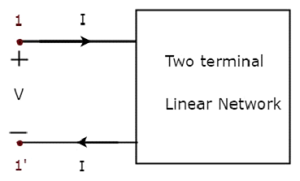
Ở đây, cặp thiết bị đầu cuối, 1 & 1 'đại diện cho một cổng. Trong trường hợp này, chúng tôi chỉ có một cổng vì nó là mạng một cổng.
Tương tự, two port networklà một cặp mạng điện hai đầu cuối, trong đó, dòng điện đi qua một đầu cuối và đi qua một đầu cuối khác của mỗi cổng. Biểu diễn mạng hai cổng được thể hiện trong hình sau.
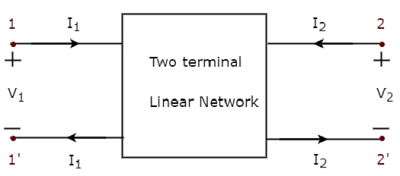
Ở đây, một cặp thiết bị đầu cuối, 1 & 1 'đại diện cho một cổng, được gọi là port1 và cặp thiết bị đầu cuối khác, 2 & 2 'đại diện cho một cổng khác, được gọi là port2.
Có four variablesV 1 , V 2 , I 1 và I 2 trong một mạng hai cổng như trong hình. Trong số đó, chúng ta có thể chọn hai biến là độc lập và hai biến khác là phụ thuộc. Vì vậy, chúng ta sẽ nhận được sáu cặp phương trình khả dĩ. Các phương trình này biểu diễn các biến phụ thuộc dưới dạng các biến độc lập. Hệ số của các biến độc lập được gọi làparameters. Vì vậy, mỗi cặp phương trình sẽ cho một bộ bốn tham số.
Hai tham số mạng cổng
Các tham số của mạng hai cổng được gọi là two port network parametershoặc đơn giản là hai tham số cổng. Sau đây là các loại tham số mạng hai cổng.
- Thông số Z
- Tham số Y
- Thông số T
- Thông số T '
- h-parameters
- g-parameters
Bây giờ, chúng ta hãy thảo luận lần lượt về hai thông số mạng cổng này.
Thông số Z
Chúng ta sẽ nhận được bộ hai phương trình sau đây bằng cách coi các biến V 1 & V 2 là phụ thuộc và I 1 & I 2 là độc lập. Hệ số của các biến độc lập, I 1 và I 2 được gọi làZ parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Các Z parameters Chúng tôi
$$Z_{11} = \frac{V_1}{I_1}, \: when \: I_2 = 0$$
$$Z_{12} = \frac{V_1}{I_2}, \: when \: I_1 = 0$$
$$Z_{21} = \frac{V_2}{I_1}, \: when \: I_2 = 0$$
$$Z_{22} = \frac{V_2}{I_2}, \: when \: I_1 = 0$$
Tham số Z được gọi là impedance parametersbởi vì đây chỉ đơn giản là tỷ số điện áp và dòng điện. Đơn vị của tham số Z là Ohm (Ω).
Chúng ta có thể tính toán hai tham số Z, Z 11 và Z 21 , bằng cách thực hiện mở mạch cổng2. Tương tự, chúng ta có thể tính toán hai tham số Z khác, Z 12 và Z 22 bằng cách thực hiện mở mạch cổng1. Do đó, các tham số Z còn được gọi làopen-circuit impedance parameters.
Tham số Y
Chúng ta sẽ nhận được bộ hai phương trình sau đây bằng cách coi các biến I 1 & I 2 là phụ thuộc và V 1 & V 2 là độc lập. Hệ số của các biến độc lập, V 1 và V 2 được gọi làY parameters.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
Các Y parameters Chúng tôi
$$Y_{11} = \frac{I_1}{V_1}, \: when \: V_2 = 0$$
$$Y_{12} = \frac{I_1}{V_2}, \: when \: V_1 = 0$$
$$Y_{21} = \frac{I_2}{V_1}, \: when \: V_2 = 0$$
$$Y_{22} = \frac{I_2}{V_2}, \: when \: V_1 = 0$$
Tham số Y được gọi là admittance parametersbởi vì đây đơn giản là tỷ lệ dòng điện và điện áp. Đơn vị của tham số Y là mho.
Chúng ta có thể tính toán hai tham số Y, Y 11 và Y 21 bằng cách làm ngắn mạch cổng2. Tương tự, chúng ta có thể tính toán hai thông số Y khác, Y 12 và Y 22 bằng cách thực hiện đoản mạch cổng1. Do đó, các tham số Y còn được gọi làshort-circuit admittance parameters.
Thông số T
Chúng ta sẽ nhận được bộ hai phương trình sau bằng cách coi các biến V 1 & I 1 là phụ thuộc và V 2 & I 2 là độc lập. Các hệ số của V 2 và I 2 được gọi làT parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
Các T parameters Chúng tôi
$$A = \frac{V_1}{V_2}, \: when \: I_2 = 0$$
$$B = -\frac{V_1}{I_2}, \: when \: V_2 = 0$$
$$C = \frac{I_1}{V_2}, \: when \: I_2 = 0$$
$$D = -\frac{I_1}{I_2}, \: when \: V_2 = 0$$
Tham số T được gọi là tham số truyền hoặc ABCD parameters. Các tham số, A và D không có bất kỳ đơn vị nào, vì đó là các tham số nhỏ hơn. Đơn vị của các tham số, B và C lần lượt là ohm và mho.
Chúng ta có thể tính toán hai tham số, A và C bằng cách thực hiện mở mạch cổng2. Tương tự, chúng ta có thể tính toán hai thông số khác, B và D bằng cách làm ngắn mạch cổng2.
Thông số T '
Chúng ta sẽ nhận được bộ hai phương trình sau bằng cách coi các biến V 2 & I 2 là phụ thuộc và V 1 & I 1 là độc lập. Các hệ số của V 1 và I 1 được gọi làT’ parameters.
$$V_2 = A' V_1 - B' I_1$$
$$I_2 = C' V_1 - D' I_1$$
Các T’ parameters Chúng tôi
$$A' = \frac{V_2}{V_1}, \: when\: I_1 = 0$$
$$B' = -\frac{V_2}{I_1}, \: when\: V_1 = 0$$
$$C' = \frac{I_2}{V_1}, \: when\: I_1 = 0$$
$$D' = -\frac{I_2}{I_1}, \: when \: V_1 = 0$$
Tham số T 'được gọi là tham số truyền nghịch đảo hoặc A’B’C’D’ parameters. Các tham số A 'và D' không có bất kỳ đơn vị nào, vì đó là các tham số nhỏ hơn. Đơn vị của các tham số, B 'và C', lần lượt là Ohm và Mho.
Chúng ta có thể tính toán hai tham số, A 'và C', bằng cách thực hiện một mạch mở của cổng1. Tương tự, chúng ta có thể tính toán hai tham số khác, B 'và D', bằng cách thực hiện đoản mạch cổng1.
thông số h
Chúng ta sẽ nhận được bộ hai phương trình sau đây bằng cách coi các biến V 1 & I 2 là phụ thuộc và I 1 & V 2 là độc lập. Hệ số của các biến độc lập, I 1 và V 2 , được gọi làh-parameters.
$$V_1 = h_{11} I_1 + h_{12} V_2$$
$$I_2 = h_{21} I_1 + h_{22} V_2$$
Các tham số h là
$$h_{11} = \frac{V_1}{I_1},\: when\: V_2 = 0$$
$$h_{12} = \frac{V_1}{V_2},\: when\: I_1 = 0$$
$$h_{21} = \frac{I_2}{I_1},\: when\: V_2 = 0$$
$$h_{22} = \frac{I_2}{V_2},\: when\: I_1 = 0$$
tham số h được gọi là hybrid parameters. Các tham số h 12 và h 21 không có bất kỳ đơn vị nào, vì chúng không có thứ nguyên. Đơn vị của các tham số, h 11 và h 22 , lần lượt là Ohm và Mho.
Chúng ta có thể tính toán hai tham số h 11 và h 21 bằng cách làm ngắn mạch cổng2. Tương tự, chúng ta có thể tính toán hai tham số khác, h 12 và h 22 bằng cách thực hiện mở mạch cổng1.
Thông số h hoặc thông số lai rất hữu ích trong các mạch mô hình bóng bán dẫn (mạng).
tham số g
Chúng ta sẽ nhận được bộ hai phương trình sau đây bằng cách coi các biến I 1 & V 2 là phụ thuộc và V 1 & I 2 là độc lập. Hệ số của các biến độc lập, V 1 và I 2 được gọi làg-parameters.
$$I_1 = g_{11} V_1 + g_{12} I_2$$
$$V_2 = g_{21} V_1 + g_{22} I_2$$
Các g-parameters Chúng tôi
$$g_{11} = \frac{I_1}{V_1},\: when\: I_2 = 0$$
$$g_{12} = \frac{I_1}{I_2},\: when\: V_1 = 0$$
$$g_{21} = \frac{V_2}{V_1},\: when\: I_2 = 0$$
$$g_{22} = \frac{V_2}{I_2},\: when \: V_1 = 0$$
tham số g được gọi là inverse hybrid parameters. Các tham số, g 12 và g 21 không có bất kỳ đơn vị nào, vì chúng là thứ nguyên nhỏ hơn. Đơn vị của các tham số, g 11 và g 22 lần lượt là mho và ohm.
Chúng ta có thể tính toán hai tham số, g 11 và g 21 bằng cách thực hiện mở mạch cổng2. Tương tự, chúng ta có thể tính toán hai thông số khác, g 12 và g 22 bằng cách thực hiện đoản mạch cổng1.
Trong chương trước, chúng ta đã thảo luận về sáu loại tham số mạng hai cổng. Bây giờ, chúng ta hãy chuyển đổi một bộ thông số mạng hai cổng thành một bộ thông số mạng hai cổng khác. Chuyển đổi này được gọi là chuyển đổi thông số mạng hai cổng hoặc đơn giản,two-port parameters conversion.
Đôi khi, có thể dễ dàng tìm thấy một tập hợp các thông số của một mạng điện nhất định một cách dễ dàng. Trong những tình huống đó, chúng ta có thể chuyển đổi các tham số này thành tập tham số cần thiết thay vì tính toán trực tiếp các tham số này với khó khăn hơn.
Bây giờ, chúng ta hãy thảo luận về một số chuyển đổi thông số hai cổng.
Quy trình chuyển đổi hai tham số cổng
Thực hiện theo các bước sau, trong khi chuyển đổi một bộ thông số mạng hai cổng thành bộ thông số mạng hai cổng khác.
Step 1 - Viết phương trình của mạng hai cổng theo các tham số mong muốn.
Step 2 - Viết phương trình của mạng hai cổng theo các tham số đã cho.
Step 3 - Sắp xếp lại các phương trình của Bước 2 sao cho chúng giống với các phương trình của Bước 1.
Step 4- Bằng cách cân bằng các phương trình tương tự của Bước1 và Bước 3, chúng ta sẽ nhận được các tham số mong muốn về các tham số đã cho. Chúng ta có thể biểu diễn các tham số này dưới dạng ma trận.
Tham số Z đến tham số Y
Ở đây, chúng ta phải biểu diễn tham số Y dưới dạng tham số Z. Vì vậy, trong trường hợp này tham số Y là tham số mong muốn và tham số Z là tham số đã cho.
Step 1 - Chúng ta biết rằng tập hợp hai phương trình sau, biểu thị một mạng hai cổng về Y parameters.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
Chúng ta có thể biểu diễn hai phương trình trên trong matrix hình thức như
$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 1
Step 2 - Chúng ta biết rằng tập hợp hai phương trình sau, biểu thị một mạng hai cổng về Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Chúng ta có thể biểu diễn hai phương trình trên trong matrix hình thức như
$$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$$
Step 3 - Chúng tôi có thể sửa đổi nó thành
$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 2
Step 4 - Bằng cách cân bằng phương trình 1 và phương trình 2, chúng ta sẽ nhận được
$$\begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} $$
$$\Rightarrow \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \frac{\begin{bmatrix}Z_{22} & -Z_{12} \\-Z_{21} & Z_{11} \end{bmatrix}}{\Delta Z}$$
Ở đâu,
$$\Delta Z = Z_{11} Z_{22} - Z_{12} Z_{21}$$
Vì vậy, chỉ bằng cách làm inverse of Z parameters matrix, chúng ta sẽ nhận được ma trận tham số Y.
Tham số Z đến tham số T
Ở đây, chúng ta phải biểu diễn tham số T dưới dạng tham số Z. Vì vậy, trong trường hợp này tham số T là tham số mong muốn và tham số Z là tham số đã cho.
Step 1 - Chúng ta biết rằng, tập hợp hai phương trình sau, đại diện cho một mạng hai cổng về mặt T parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
Step 2 - Chúng ta biết rằng tập hợp hai phương trình sau, biểu thị một mạng hai cổng về Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Step 3 - Chúng ta có thể sửa đổi phương trình trên thành
$$\Rightarrow V_2 - Z_{22} I_2 = Z_{21} I_1$$
$$\Rightarrow I_1 = \lgroup \frac{1}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{22}}{Z_{21}} \rgroup I_2$$
Step 4 - Phương trình trên có dạng $I_1 = CV_2 − DI_2$. Đây,
$$C = \frac{1}{Z_{21}}$$
$$D = \frac{Z_{22}}{Z_{21}}$$
Step 5 - Thay thế $I_1$ giá trị của Bước 3 trong $V_1$ phương trình của Bước 2.
$$V_1 = Z_{11} \lbrace \lgroup \frac {1}{Z_{12}} \rgroup V_2 - \lgroup \frac {Z_{22}}{Z_{21}} \rgroup I_2 \rbrace + Z_{12} I_2$$
$$\Rightarrow V_1 = \lgroup \frac {Z_{11}}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}} \rgroup I_2$$
Step 6 - Phương trình trên có dạng $V_1 = AV_2 − BI_2$. Đây,
$$A = \frac{Z_{11}}{Z_{21}}$$
$$B = \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}}$$
Step 7 - Do đó, T parameters matrix Là
$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{Z_{11}}{Z_{21}} & \frac{Z_{11}Z_{22} - Z_{12}Z_{21}}{Z_{21}} \\\frac{1}{Z_{21}} & \frac{Z_{22}}{Z_{21}} \end{bmatrix}$$
Tham số Y đến tham số Z
Ở đây, chúng ta phải biểu diễn tham số Z dưới dạng tham số Y. Vì vậy, trong trường hợp này tham số Z là tham số mong muốn và tham số Y là tham số đã cho.
Step 1 - Chúng ta biết rằng, phương trình ma trận sau của mạng hai cổng liên quan đến các tham số Z là
$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 3
Step 2 - Chúng ta biết rằng, phương trình ma trận sau của mạng hai cổng liên quan đến các tham số Y là
$$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$$
Step 3 - Chúng tôi có thể sửa đổi nó thành
$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 4
Step 4 - Bằng cách cân bằng phương trình 3 và phương trình 4, chúng ta sẽ nhận được
$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1}$$
$$\Rightarrow \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \frac{\begin{bmatrix}Y_{22} & - Y_{12} \\- Y_{21} & Y_{11} \end{bmatrix}}{\Delta Y}$$
Ở đâu,
$$\Delta Y = Y_{11} Y_{22} - Y_{12} Y_{21}$$
Vì vậy, chỉ bằng cách làm inverse of Y parameters matrix, chúng ta sẽ nhận được ma trận tham số Z.
Tham số Y thành tham số T
Ở đây, chúng ta phải biểu diễn tham số T dưới dạng tham số Y. Vì vậy, trong trường hợp này, tham số T là tham số mong muốn và tham số Y là tham số đã cho.
Step 1 - Chúng ta biết rằng, tập hợp hai phương trình sau, đại diện cho một mạng hai cổng về mặt T parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
Step 2 - Chúng ta biết rằng bộ hai phương trình sau đây của hai mạng cổng liên quan đến tham số Y.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
Step 3 - Chúng ta có thể sửa đổi phương trình trên thành
$$\Rightarrow I_2 - Y_{22} V_2 = Y_{21} V_1$$
$$\Rightarrow V_1 = \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2$$
Step 4 - Phương trình trên có dạng $V_1 = AV_2 − BI_2$. Đây,
$$A = \frac{- Y_{22}}{Y_{21}}$$
$$B = \frac{-1}{Y_{21}}$$
Step 5 - Thay thế $V_1$ giá trị của Bước 3 trong $I_1$ phương trình của Bước 2.
$$I_1 = Y_{11} \lbrace \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2 \rbrace + Y_{12} V_2$$
$$\Rightarrow I_1 = \lgroup \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{- Y_{11}} {Y_{21}} \rgroup I_2$$
Step 6 - Phương trình trên có dạng $I_1 = CV_2 − DI_2$. Đây,
$$C = \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}}$$
$$D = \frac{- Y_{11}} {Y_{21}}$$
Step 7 - Do đó, T parameters matrix Là
$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{-Y_{22}}{Y_{21}} & \frac{-1}{Y_{21}} \\\frac{Y_{12}Y_{21} - Y_{11}Y_{22}}{Y_{21}} & \frac{-Y_{11}}{Y_{21}} \end{bmatrix}$$
Tham số T thành tham số h
Ở đây, chúng ta phải biểu diễn tham số h dưới dạng tham số T. Vì vậy, trong trường hợp này, hparameters là các tham số mong muốn và tham số T là các tham số đã cho.
Step 1 - Chúng tôi biết điều đó, những điều sau h-parameters của mạng hai cổng.
$$h_{11} = \frac{V_1}{I_1}, \: when \: V_2 = 0$$
$$h_{12} = \frac{V_1}{V_2}, \: when \: I_1 = 0$$
$$h_{21} = \frac{I_2}{I_1}, \: when \: V_2 = 0$$
$$h_{22} = \frac{I_2}{V_2}, \: when \: I_1 = 0$$
Step 2 - Chúng ta biết rằng bộ hai phương trình sau của hai mạng cổng liên quan đến T parameters.
$V_1 = A V_2 - B I_2$Equation 5
$I_1 = C V_2 - D I_2$Equation 6
Step 3 - Thay thế $V_2 = 0$ trong các phương trình trên để tìm hai tham số h, $h_{11}$ và $h_{21}$.
$$\Rightarrow V_1 = -B I_2$$
$$\Rightarrow I_1 = -D I_2$$
Thay thế, $V_1$ và $I_1$ các giá trị trong tham số h, $h_{11}$.
$$h_{11} = \frac{-B I_2}{-D I_2}$$
$$\Rightarrow h_{11} = \frac{B}{D}$$
Người thay thế $I_1$ giá trị trong tham số h $h_{21}$.
$$h_{21} = \frac{I_2}{- D I_2}$$
$$\Rightarrow h_{21} = - \frac{1}{D}$$
Step 4 - Thay thế $I_1 = 0$ trong phương trình thứ hai của bước 2 để tìm tham số h $h_{22}$.
$$0 = C V_2 - D I_2$$
$$\Rightarrow C V_2 = D I_2$$
$$\Rightarrow \frac{I_2}{V_2} = \frac{C}{D}$$
$$\Rightarrow h_{22} = \frac{C}{D}$$
Step 5 - Thay thế $I_2 = \lgroup \frac{C}{D} \rgroup V_2$ trong phương trình đầu tiên của bước 2 để tìm tham số h, $h_{12}$.
$$V_1 = A V_2 - B \lgroup \frac{C}{D} \rgroup V_2$$
$$\Rightarrow V_1 = \lgroup \frac{AD - BC}{D} \rgroup V_2$$
$$\Rightarrow \frac{V_1}{V_2} = \frac{AD - BC}{D}$$
$$\Rightarrow h_{12} = \frac{AD - BC}{D}$$
Step 6 - Do đó, ma trận tham số h là
$$\begin{bmatrix}h_{11} & h_{12} \\h_{21} & h_{22} \end{bmatrix} = \begin{bmatrix}\frac{B}{D} & \frac{AD - BC}{D} \\-\frac{1}{D} & \frac{C}{D} \end{bmatrix}$$
tham số h đến tham số Z
Ở đây, chúng ta phải biểu diễn các tham số Z dưới dạng tham số h. Vì vậy, trong trường hợp này, tham số Z là tham số mong muốn và tham số h là tham số đã cho.
Step 1 - Chúng ta biết rằng, bộ hai phương trình sau của hai mạng cổng liên quan đến Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Step 2 - Chúng ta biết rằng, tập hợp hai phương trình sau của mạng hai cổng liên quan đến h-parameters.
$$V_1 = h_{11} I_1 + h_{12} V_2$$
$$I_2 = h_{21} I_1 + h_{22} V_2$$
Step 3 - Chúng ta có thể sửa đổi phương trình trên thành
$$\Rightarrow I_2 - h_{21} I_1 = h_{22} V_2$$
$$\Rightarrow V_2 = \frac{I_2 - h_{21} I_1}{h_{22}}$$
$$\Rightarrow V_2 = \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2$$
Phương trình trên có dạng $V_2 = Z_{21} I_1 + Z_{22} I_2. Here,$
$$Z_{21} = \frac{-h_{21}}{h_{22}}$$
$$Z_{22} = \frac{1}{h_{22}}$$
Step 4- Thay giá trị V 2 vào phương trình đầu tiên của bước 2.
$$V_1 = h_{11} I_1 + h_{21} \lbrace \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2 \rbrace$$
$$\Rightarrow V_1 = \lgroup \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{h_{12}}{h_{22}} \rgroup I_2$$
Phương trình trên có dạng $V_1 = Z_{11}I_1 + Z_{12}I_2$. Đây,
$$Z_{11} = \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}}$$
$$Z_{12} = \frac{h_{12}}{h_{22}}$$
Step 5 - Do đó, ma trận tham số Z là
$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}\frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} & \frac{h_{12}}{h_{22}} \\\frac{-h_{21}}{h_{22}} & \frac{1}{h_{22}} \end{bmatrix}$$
Bằng cách này, chúng ta có thể chuyển đổi một tập tham số thành tập tham số khác.
Bộ lọc như tên cho thấy, chúng lọc các thành phần tần số. Điều đó có nghĩa là, chúng cho phép một số thành phần tần số nhất định và / hoặc từ chối một số thành phần tần số khác.
Trong chương này, chúng ta hãy thảo luận về passive filters. Đó là những mạch điện hoặc mạng có các phần tử thụ động như điện trở, cuộn cảm và tụ điện.
Các loại bộ lọc
Bộ lọc chủ yếu được phân loại thành four typesdựa trên dải tần số cho phép và / hoặc dải tần số từ chối. Sau đây là các loại bộ lọc.
- Bộ lọc thông thấp
- Bộ lọc thông cao
- Bộ lọc băng thông
- Bộ lọc Dừng băng tần
Bộ lọc thông thấp
Bộ lọc thông thấp như tên cho thấy, nó chỉ cho phép (vượt qua) low frequencycác thành phần. Điều đó có nghĩa là, nó từ chối (chặn) tất cả các thành phần tần số cao khác.
Miền s circuit diagram (mạng) của Bộ lọc thông thấp được hiển thị trong hình sau.
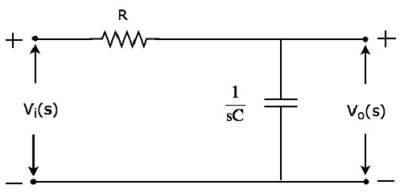
Nó bao gồm hai phần tử thụ động điện trở và tụ điện, được kết nối trong series. Điện áp đầu vào được áp dụng trên toàn bộ tổ hợp này và đầu ra được coi là điện áp trên tụ điện.
Đây, $V_i(s)$ và $V_o(s)$ là các biến đổi Laplace của điện áp đầu vào, $v_i(t)$ và điện áp đầu ra, $v_o(t)$ tương ứng.
Các transfer function của mạng trên là
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{\frac{1}{sC}}{R + \frac{1}{sC}}$$
$$\Rightarrow H(s) = \frac{1}{1 + sCR}$$
Thay thế, $s = j \omega$ trong phương trình trên.
$$H(j \omega) = \frac{1}{1 + j \omega CR}$$
Tầm quan trọng của hàm truyền là
$$|H(j \omega)| = \frac{1}{\sqrt{(1 + (\omega CR)^2}}$$
Tại ω = 0, độ lớn của hàm truyền bằng 1.
Tại $\omega = \frac{1}{CR}$, độ lớn của hàm truyền bằng 0,707.
Tại ω = ∞, độ lớn của hàm truyền bằng 0.
Do đó, độ lớn của hàm truyền của Low pass filtersẽ thay đổi từ 1 đến 0 vì ω thay đổi từ 0 đến ∞.
Bộ lọc thông cao
Bộ lọc thông cao như tên cho thấy, nó chỉ cho phép (vượt qua) high frequencycác thành phần. Điều đó có nghĩa là, nó từ chối (chặn) tất cả các thành phần tần số thấp.
Miền s circuit diagram (mạng) của bộ lọc Thông cao được hiển thị trong hình sau.
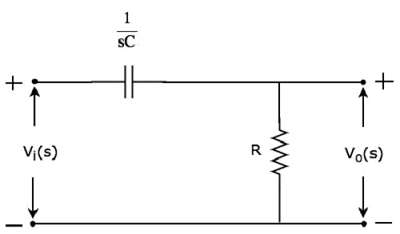
Nó bao gồm hai phần tử thụ động là tụ điện và điện trở, được kết nối trong series. Điện áp đầu vào được áp dụng trên toàn bộ tổ hợp này và đầu ra được coi là điện áp trên điện trở.
Đây, $V_i(s)$ và $V_o(s)$ là các biến đổi Laplace của điện áp đầu vào, $v_i(t)$ và điện áp đầu ra, $v_o(t)$ tương ứng.
Các transfer function của mạng trên là
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC}}$$
$$\Rightarrow H(s) = \frac{sCR}{1 + sCR}$$
Thay thế, $s = j \omega$ trong phương trình trên.
$$H(j \omega) = \frac{j \omega CR}{1 + j \omega CR}$$
Tầm quan trọng của hàm truyền là
$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 + (\omega CR)^2}}$$
Tại ω = 0, độ lớn của hàm truyền bằng 0.
Tại $\omega = \frac{1}{CR}$, độ lớn của hàm truyền bằng 0,707.
Tại ω = ∞, độ lớn của hàm truyền bằng 1.
Do đó, độ lớn của hàm truyền của High pass filtersẽ thay đổi từ 0 đến 1 vì ω thay đổi từ 0 đến ∞.
Bộ lọc băng thông
Bộ lọc băng thông như tên cho thấy, nó allows (vượt qua) chỉ one bandtần số. Nói chung, dải tần này nằm giữa dải tần thấp và dải tần cao. Điều đó có nghĩa là bộ lọc này từ chối (chặn) cả các thành phần tần số thấp và cao.
Miền s circuit diagram (mạng) của bộ lọc băng thông được hiển thị trong hình sau.
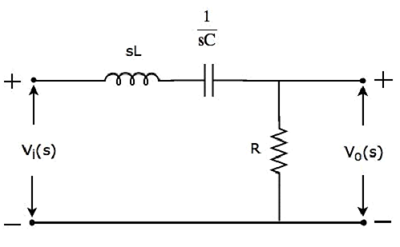
Nó bao gồm ba phần tử thụ động cuộn cảm, tụ điện và điện trở, được kết nối trong series. Điện áp đầu vào được áp dụng trên toàn bộ tổ hợp này và đầu ra được coi là điện áp trên điện trở.
Đây, $V_i(s)$ và $V_o(s)$ là các biến đổi Laplace của điện áp đầu vào, $v_i(t)$ và điện áp đầu ra, $v_o(t)$ tương ứng.
Các transfer function của mạng trên là
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC} + sL}$$
$$\Rightarrow H(s) = \frac{s CR}{s^2 LC + sCR + 1}$$
Người thay thế $s = j \omega$ trong phương trình trên.
$$H(j \omega) = \frac{j \omega CR}{1 - \omega^2 LC + j \omega CR}$$
Tầm quan trọng của hàm truyền là
$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$
Tại ω = 0, độ lớn của hàm truyền bằng 0.
Tại $\omega = \frac{1}{\sqrt{LC}}$, độ lớn của hàm truyền bằng 1.
Tại ω = ∞, độ lớn của hàm truyền bằng 0.
Do đó, độ lớn của hàm truyền của Band pass filtersẽ thay đổi từ 0 đến 1 & 1 đến 0 khi ω thay đổi từ 0 đến ∞.
Bộ lọc Dừng băng tần
Bộ lọc dừng băng tần như tên cho thấy, nó từ chối (chặn) chỉ một dải tần số. Nói chung, dải tần này nằm giữa dải tần thấp và dải tần cao. Điều đó có nghĩa là, bộ lọc này cho phép (vượt qua) cả các thành phần tần số thấp và cao.
Miền s (mạng) của circuit diagramvà bộ lọc dừng được hiển thị trong hình sau.
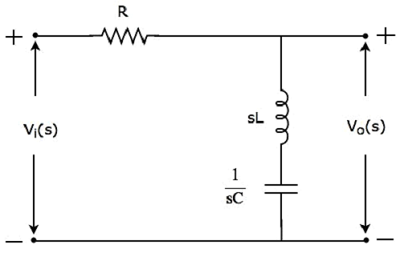
Nó bao gồm ba phần tử thụ động điện trở, cuộn cảm và tụ điện, được kết nối trong series. Điện áp đầu vào được áp dụng trên toàn bộ sự kết hợp này và đầu ra được coi là điện áp trên sự kết hợp của cuộn cảm và tụ điện.
Đây, $V_i(s)$ và $V_o(s)$ là các biến đổi Laplace của điện áp đầu vào, $v_i(t)$ và điện áp đầu ra, $v_o(t)$ tương ứng.
Các transfer function của mạng trên là
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{sL + \frac{1}{sC}}{R + sL + \frac{1}{sC}}$$
$$\Rightarrow H(s) = \frac{s^2 LC + 1}{s^2 LC + sCR + 1}$$
Thay thế, $s = j \omega$ trong phương trình trên.
$$H(j \omega) = \frac{1 - \omega^2 LC}{1 - \omega^2 LC + j \omega CR}$$
Tầm quan trọng của hàm truyền là
$$|H(j \omega)| = \frac{1 - \omega^2 LC}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$
Tại ω = 0, độ lớn của hàm truyền bằng 1.
Tại $\omega = \frac{1}{\sqrt{LC}}$, độ lớn của hàm truyền bằng 0.
Tại ω = ∞, độ lớn của hàm truyền bằng 1.
Do đó, độ lớn của hàm truyền của Band stop filtersẽ thay đổi từ 1 đến 0 & 0 thành 1 khi ω thay đổi từ 0 đến ∞.