Nguyên tắc phân chia số lượng điện
Trong chương này, chúng ta hãy thảo luận về hai nguyên tắc phân chia sau đây của các đại lượng điện.
- Nguyên tắc phân chia hiện tại
- Nguyên tắc phân chia điện áp
Nguyên tắc phân chia hiện tại
Khi hai hoặc nhiều phần tử thụ động được kết nối song song, lượng dòng điện chạy qua mỗi phần tử sẽ divided (được chia sẻ) với nhau từ dòng điện đang đi vào nút.
Hãy xem xét những điều sau circuit diagram.
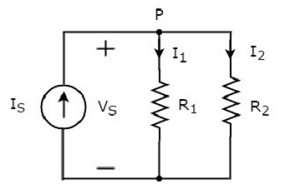
Sơ đồ mạch trên gồm một nguồn dòng vào IS mắc song song hai điện trở R1 và R2. Điện áp trên mỗi phần tử làVS. Dòng điện chạy qua các điện trởR1 và R2 Chúng tôi I1 và I2 tương ứng.
Các KCL equation tại nút P sẽ là
$$ I_S = I_1 + I_2 $$
Thay $ I_1 = \ frac {V_S} {R_1} $ và $ I_2 = \ frac {V_S} {R_2} $ trong phương trình trên.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} = V_S \ lgroup \ frac {R_2 + R_1} {R_1 R_2} \ rgroup $$
$$ \ Rightarrow V_S = I_S \ lgroup \ frac {R_1R_2} {R_1 + R_2} \ rgroup $$
Thay giá trị của V S bằng $ I_1 = \ frac {V_S} {R_1} $.
$$ I_1 = \ frac {I_S} {R_1} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_1 = I_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
Thay giá trị của V S bằng $ I_2 = \ frac {V_S} {R_2} $.
$$ I_2 = \ frac {I_S} {R_2} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Từ phương trình I 1 và I 2 , chúng ta có thể tổng quát rằng dòng điện chạy qua bất kỳ phần tử thụ động nào có thể được tìm thấy bằng cách sử dụng công thức sau.
$$ I_N = I_S \ lgroup \ frac {Z_1 \ rVert Z_2 \ rVert ... \ rVert Z_ {N-1}} {Z_1 + Z_2 + ... + Z_N} \ rgroup $$
Điều này được gọi là current division principle và nó có thể áp dụng, khi hai hoặc nhiều phần tử thụ động được kết nối song song và chỉ có một dòng điện đi vào nút.
Ở đâu,
I N là dòng điện chạy qua phần tử thụ động của nhánh thứ N.
I S là dòng điện đầu vào đi vào nút.
Z 1 , Z 2 ,…, Z N lần lượt là trở kháng của nhánh thứ 1 , nhánh thứ 2 ,…, nhánh thứ N.
Nguyên tắc phân chia điện áp
Khi hai hoặc nhiều phần tử thụ động mắc nối tiếp, lượng điện áp hiện tại trên mỗi phần tử sẽ divided (được chia sẻ) giữa chúng với nhau từ điện áp có sẵn trên toàn bộ sự kết hợp đó.
Hãy xem xét những điều sau circuit diagram.
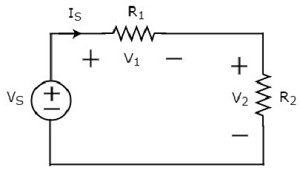
Sơ đồ mạch điện trên gồm nguồn hiệu điện thế V S mắc nối tiếp với hai điện trở R 1 và R 2 . Dòng điện chảy qua các yếu tố này là tôi S . Điện áp rơi trên điện trở R 1 và R 2 là V 1 và V 2 tương ứng.
Các KVL equation xung quanh vòng lặp sẽ là
$$ V_S = V_1 + V_2 $$
Thay V 1 = I S R 1 và V 2 = I S R 2 vào phương trình trên
$$ V_S = I_S R_1 + I_S R_2 = I_S (R_1 + R_2) $$
$$ I_S = \ frac {V_S} {R_1 + R_2} $$
Thay giá trị của I S vào V 1 = I S R 1 .
$$ V_1 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_1 $$
$$ \ Rightarrow V_1 = V_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Thay giá trị của I S vào V 2 = I S R 2 .
$$ V_2 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_2 $$
$$ \ Rightarrow V_2 = V_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
Từ phương trình V 1 và V 2 , chúng ta có thể tổng quát rằng điện áp trên bất kỳ phần tử thụ động nào có thể được tìm thấy bằng cách sử dụng công thức sau.
$$ V_N = V_S \ lgroup \ frac {Z_N} {Z_1 + Z_2 + .... + Z_N} \ rgroup $$
Điều này được gọi là voltage division principle và nó có thể áp dụng được, khi hai hoặc nhiều phần tử thụ động được mắc nối tiếp và chỉ có một điện áp khả dụng trên toàn bộ tổ hợp.
Ở đâu,
V N là điện áp trên N thứ yếu tố thụ động.
V S là điện áp đầu vào, có mặt trên toàn bộ tổ hợp các phần tử thụ động nối tiếp.
Z 1 , Z 2 ,…, Z 3 lần lượt là trở kháng của phần tử bị động thứ 1 , phần tử bị động thứ 2 ,…, phần tử bị động thứ N.