Lý thuyết mạng - Phân tích Nodal
Có hai phương pháp cơ bản được sử dụng để giải quyết bất kỳ mạng điện nào: Nodal analysis và Mesh analysis. Trong chương này, chúng ta hãy thảo luận vềNodal analysis phương pháp.
Trong phân tích Nodal, chúng tôi sẽ xem xét điện áp của nút đối với Ground. Do đó, phân tích Nodal còn được gọi làNode-voltage method.
Quy trình Phân tích Nodal
Làm theo các bước sau khi giải quyết bất kỳ mạng hoặc mạch điện nào bằng phân tích Nodal.
Step 1 - Xác định principal nodes và chọn một trong số họ là reference node. Chúng tôi sẽ coi nút tham chiếu đó là Mặt đất.
Step 2 - Gắn nhãn node voltages đối với Ground từ tất cả các nút chính ngoại trừ nút tham chiếu.
Step 3 - Viết nodal equationstại tất cả các nút chính ngoại trừ nút tham chiếu. Phương trình Nodal thu được bằng cách áp dụng KCL trước rồi đến định luật Ohm.
Step 4 - Giải các phương trình nút thu được ở Bước 3 để có được điện áp nút.
Bây giờ, chúng ta có thể tìm thấy dòng điện chạy qua bất kỳ phần tử nào và điện áp trên bất kỳ phần tử nào có trong mạng nhất định bằng cách sử dụng điện áp nút.
Thí dụ
Tìm cường độ dòng điện chạy qua điện trở 20 Ω của đoạn mạch sau sử dụng Nodal analysis.
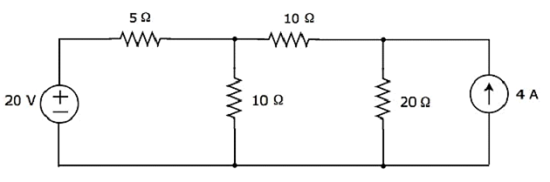
Step 1 - Có three principle nodestrong đoạn mạch trên. Chúng được gắn nhãn là 1, 2 và 3 trong hình sau.
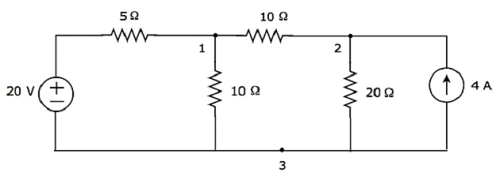
Trong hình trên, hãy xem xét node 3 làm nút tham chiếu (Ground).
Step 2- Các điện áp của nút, V 1 và V 2 , được ghi nhãn trong hình sau.
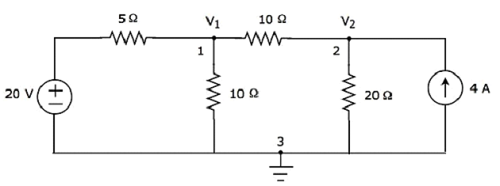
Trong hình trên, V 1 là điện áp từ nút 1 đối với đất và V 2 là điện áp từ nút 2 đối với đất.
Step 3 - Trong trường hợp này, chúng tôi sẽ nhận được two nodal equations, vì có hai nút chính, 1 và 2, khác với Ground. Khi chúng ta viết phương trình nút tại một nút, giả sử tất cả các dòng điện đang rời khỏi nút mà hướng của dòng điện không được đề cập và điện áp của nút đó lớn hơn điện áp của nút khác trong mạch.
Các nodal equation tại nút 1 là
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1 - V_2} {10} = 0 $$
$$ \ Rightarrow \ frac {2 V_1 - 40 + V_1 + V_1 - V_2} {10} = 0 $$
$$ \ Rightarrow 4V_1 - 40 - V_2 = 0 $$
$ \ Rightarrow V_2 = 4V_1 - 40 $ Equation 1
Các nodal equation ở nút 2 là
$$ - 4 + \ frac {V_2} {20} + \ frac {V_2 - V_1} {10} = 0 $$
$$ \ Rightarrow \ frac {-80 + V_2 + 2V_2 - 2V_2} {20} = 0 $$
$ \ Rightarrow 3V_2 - 2V_1 = 80 $ Equation 2
Step 4- Tìm hiệu điện thế nút, V 1 và V 2 bằng cách giải phương trình 1 và phương trình 2.
Thay thế phương trình 1 bằng phương trình 2.
$$ 3 (4 V_1 - 40) - 2 V_1 = 80 $$
$$ \ Rightarrow 12 V_1 - 120 - 2V_1 = 80 $$
$$ \ Rightarrow 10 V_1 = 200 $$
$$ \ Rightarrow V_1 = 20V $$
Thay V 1 = 20 V trong phương trình 1.
$$ V_2 = 4 (20) - 40 $$
$$ \ Rightarrow V_2 = 40V $$
Vì vậy, chúng tôi nhận được điện áp nút V 1 và V 2 là20 V và 40 V tương ứng.
Step 5- Hiệu điện thế trên điện trở 20 Ω không là gì khác ngoài điện áp nút V 2 và nó bằng 40 V. Bây giờ, chúng ta có thể tìm dòng điện chạy qua điện trở 20 Ω bằng cách sử dụng định luật Ôm.
$$ I_ {20 \ Omega} = \ frac {V_2} {R} $$
Thay các giá trị của V 2 và R vào phương trình trên.
$$ I_ {20 \ Omega} = \ frac {40} {20} $$
$$ \ Rightarrow I_ {20 \ Omega} = 2A $$
Do đó, cường độ dòng điện chạy qua điện trở 20 Ω của đoạn mạch đã cho là 2 A.
Note- Từ ví dụ trên, chúng ta có thể kết luận rằng chúng ta phải giải 'n' phương trình nút, nếu mạch điện có 'n' nút chính (trừ nút tham chiếu). Do đó, chúng ta có thể chọn phân tích Nodal khinumber of principal nodes (ngoại trừ nút tham chiếu) ít hơn số lượng mắt lưới của bất kỳ mạch điện nào.