Vấn đề ví dụ về mạch tương đương

Trong chương trước, chúng ta đã thảo luận về các mạch tương đương của kết hợp nối tiếp và kết hợp song song riêng lẻ. Trong chương này, chúng ta hãy giải quyết một vấn đề ví dụ bằng cách xem xét cả chuỗi và kết hợp song song của các phần tử bị động tương tự.

Thí dụ

Hãy để chúng tôi tìm equivalent resistance qua các đầu cuối A & B của mạng điện sau.

Chúng ta sẽ nhận được điện trở tương đương trên các đầu cuối A & B bằng cách thu nhỏ mạng trên thành một điện trở duy nhất giữa hai đầu cuối đó. Đối với điều này, chúng ta phảiidentify the combination of resistors được kết nối ở dạng nối tiếp và dạng song song rồi tìm điện trở tương đương của dạng tương ứng trong mỗi bước.

Mạng điện đã cho là modified thành dạng sau như hình sau.

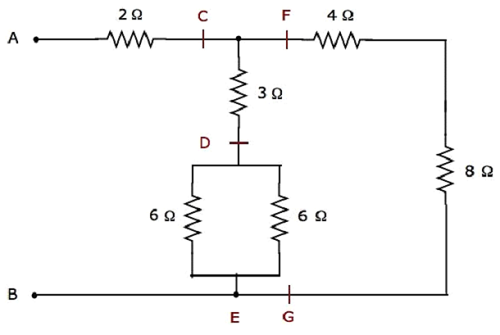
Trong hình trên, các chữ cái, C đến G, được sử dụng để ghi nhãn các thiết bị đầu cuối khác nhau.

Step 1 - Trong mạng trên, hai 6 Ω resistors được kết nối trong parallel. Vì vậy, điện trở tương đương giữa D & E sẽ là 3 Ω. Điều này có thể đạt được bằng cách thực hiện đơn giản hóa sau đây.

$$ R_ {DE} = \ frac {6 \ times 6} {6 + 6} = \ frac {36} {12} = 3 \ Omega $$

Trong mạng trên, các điện trở 4 Ω và 8 Ω được kết nối trong series. Vì vậy, điện trở tương đương giữa F & G sẽ là 12 Ω. Điều này có thể đạt được bằng cách thực hiện đơn giản hóa sau đây.

$$ R_ {FG} = 4 + 8 = 12 \ Omega $$

Step 2 - Điện đơn giản network after Step 1 được hiển thị trong hình sau.

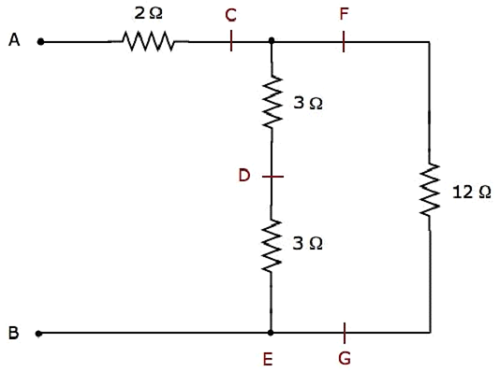
Trong mạng trên, hai 3 Ω resistors được kết nối trong series. Vì vậy, điện trở tương đương giữa C & E sẽ là6 Ω. Điều này có thể đạt được bằng cách thực hiện đơn giản hóa sau đây.

$$ R_ {CE} = 3 + 3 = 6 \ Omega $$

Step 3 - Điện đơn giản network after Step 2 được hiển thị trong hình sau.

Trong mạng trên, các điện trở 6 Ω và 12 Ω được kết nối trong parallel. Vì vậy, điện trở tương đương giữa C & B sẽ là 4 Ω. Điều này có thể đạt được bằng cách thực hiện đơn giản hóa sau đây.

$$ R_ {CB} = \ frac {6 \ times 12} {6 + 12} = \ frac {72} {18} = 4 \ Omega $$

Step 4 - Điện đơn giản network after Step 3 được hiển thị trong hình sau.

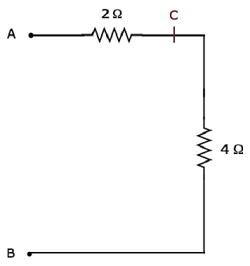
Trong mạng trên, các điện trở 2 Ω và 4 Ω được kết nối trong seriesgiữa các cực A & B. Vì vậy, điện trở tương đương giữa A & B sẽ là 6 Ω. Điều này có thể đạt được bằng cách thực hiện đơn giản hóa sau đây.

$$ R_ {AB} = 2 + 4 = 6 \ Omega $$

Do đó, điện trở tương đương giữa các đầu nối A và B của mạng điện đã cho là 6 Ω.