Lý thuyết mạng - Định luật Kirchhoff
Các phần tử mạng có thể là một trong số active hoặc là passivekiểu. Bất kỳ mạch điện hoặc mạng nào đều chứa một trong hai loại phần tử mạng này hoặc kết hợp cả hai.
Bây giờ, chúng ta hãy thảo luận về hai luật sau đây, chúng thường được biết đến là Kirchhoff’s laws.
- Luật hiện hành của Kirchhoff
- Định luật điện áp Kirchhoff
Luật hiện hành của Kirchhoff
Định luật hiện tại của Kirchhoff (KCL) phát biểu rằng tổng đại số của dòng điện đi (hoặc đi vào) một nút bằng không.
A Nodelà một điểm mà hai hoặc nhiều phần tử mạch được kết nối với nó. Nếu chỉ có hai phần tử mạch được kết nối với một nút, thì nó được cho là nút đơn giản. Nếu ba hoặc nhiều phần tử mạch được kết nối với một nút, thì nó được cho làPrincipal Node.
Mathematically, KCL có thể được đại diện là
$$ \ displaystyle \ sum \ limit_ {m = 1} ^ M I_m = 0 $$
Ở đâu,
Imlà dòng nhánh thứ m rời khỏi nút.
M là số nhánh được kết nối với một nút.
Tuyên bố trên của KCLcũng có thể được biểu thị bằng "tổng đại số của dòng điện đi vào một nút bằng tổng đại số của dòng điện ra khỏi một nút". Hãy để chúng tôi kiểm chứng nhận định này qua ví dụ sau.
Thí dụ
Viết KCL equation tại nút P của hình sau.
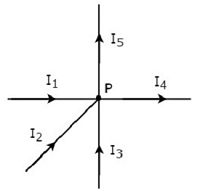
Trong hình trên, các dòng nhánh I 1 , I 2 và I 3 làentering tại nút P. Vì vậy, hãy xem xét các dấu hiệu tiêu cực cho ba dòng điện này.
Trong hình trên, các dòng nhánh I 4 và I 5 làleaving từ nút P. Vì vậy, hãy xem xét các dấu hiệu tích cực cho hai dòng điện này.
Các KCL equation tại nút P sẽ là
$$ - I_1 - I_2 - I_3 + I_4 + I_5 = 0 $$
$$ \ Rightarrow I_1 + I_2 + I_3 = I_4 + I_5 $$
Trong phương trình trên, bên trái biểu thị tổng dòng điện đi vào, trong khi bên tay phải biểu thị tổng dòng điện đi ra.
Trong hướng dẫn này, chúng ta sẽ xem xét dấu tích cực khi dòng điện rời khỏi một nút và dấu âm khi nó đi vào một nút. Tương tự, bạn có thể xem xét dấu âm khi dòng điện rời khỏi một nút và dấu tích cực khi nó đi vào một nút. Trong cả hai trường hợp,result will be same.
Note - KCL độc lập với bản chất của các phần tử mạng được kết nối với một nút.
Định luật điện áp Kirchhoff
Định luật Điện áp của Kirchhoff (KVL) phát biểu rằng tổng đại số của các điện áp xung quanh một vòng lặp hoặc lưới bằng không.
A Looplà một đường dẫn kết thúc tại cùng một nút nơi nó bắt đầu. Ngược lại, mộtMesh là một vòng lặp không chứa bất kỳ vòng lặp nào khác bên trong nó.
Về mặt toán học, KVL có thể được biểu diễn dưới dạng
$$ \ displaystyle \ sum \ limit_ {n = 1} ^ N V_n = 0 $$
Ở đâu,
Vnlà điện áp của phần tử thứ n trong một vòng lặp (lưới).
N là số phần tử mạng trong vòng lặp (lưới).
Tuyên bố trên của KVLcũng có thể được biểu thị bằng "tổng đại số của các nguồn điện áp bằng tổng đại số của điện áp rơi trong một vòng lặp." Hãy để chúng tôi xác minh tuyên bố này với sự trợ giúp của ví dụ sau.
Thí dụ
Viết KVL equation xung quanh vòng lặp của đoạn mạch sau.
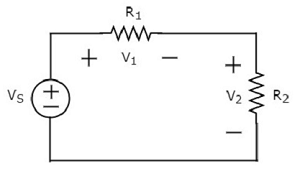
Sơ đồ mạch điện trên gồm nguồn hiệu điện thế V S mắc nối tiếp với hai điện trở R 1 và R 2 . Điện áp rơi trên điện trở R 1 và R 2 là V 1 và V 2 tương ứng.
Ứng dụng KVL xung quanh vòng lặp.
$$ V_S - V_1 - V_2 = 0 $$
$$ \ Rightarrow V_S = V_1 + V_2 $$
Trong phương trình trên, số hạng bên trái biểu thị nguồn điện áp đơn VS. Trong khi đó, phía bên phải đại diện chosum of voltage drops. Trong ví dụ này, chúng tôi chỉ xem xét một nguồn điện áp. Đó là lý do tại sao phía bên trái chỉ chứa một số hạng. Nếu chúng ta xem xét nhiều nguồn điện áp, thì phía bên trái chứa tổng các nguồn điện áp.
Trong hướng dẫn này, chúng tôi coi dấu hiệu của điện áp của mỗi phần tử là cực của thiết bị đầu cuối thứ hai hiện diện trong khi di chuyển quanh vòng lặp. Tương tự, bạn có thể coi dấu hiệu của mỗi điện áp là cực tính của đầu cuối đầu tiên hiện diện trong khi di chuyển quanh vòng lặp. Trong cả hai trường hợp,result will be same.
Note - KVL không phụ thuộc vào bản chất của các phần tử mạng có trong một vòng lặp.