Định lý truyền công suất cực đại

Lượng điện năng mà tải nhận được là một thông số quan trọng trong các ứng dụng điện và điện tử. Trong mạch điện một chiều, chúng ta có thể biểu diễn tải bằng một điện trở có điện trở R _L ohms. Tương tự, trong mạch điện xoay chiều, chúng ta có thể biểu diễn nó bằng một tải phức tạp có trở kháng Z _L ohms.

Maximum power transfer theorem nói rằng nguồn điện áp một chiều sẽ chỉ cung cấp công suất cực đại cho biến trở tải khi điện trở tải bằng điện trở nguồn.

Tương tự, Maximum power transfer theorem nói rằng nguồn điện áp xoay chiều sẽ chỉ cung cấp công suất cực đại cho tải phức biến đổi khi trở kháng tải bằng tổng trở liên hợp của nguồn.

Trong chương này, chúng ta hãy thảo luận về định lý truyền công suất cực đại cho mạch điện một chiều.

Chứng minh Định lý Truyền Công suất Cực đại

Thay thế bất kỳ mạng hoặc mạch tuyến tính hai đầu cuối nào ở phía bên trái của biến trở tải có điện trở R _L ohms bằng mạch tương đương của Thevenin. Chúng ta biết rằng mạch tương đương của Thevenin giống như một nguồn điện áp thực tế.

Khái niệm này được minh họa trong các hình sau.

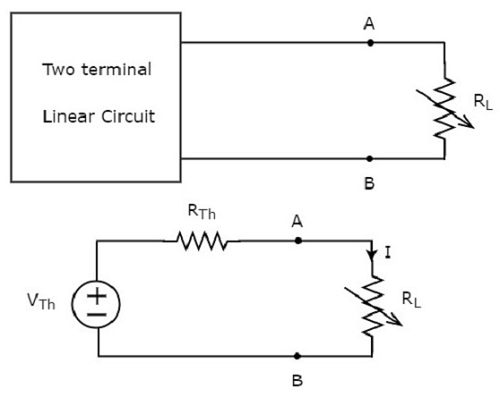
Công suất tiêu tán trên điện trở tải là

$$ P_L = I ^ 2 R_L $$

Thay $ I = \ frac {V_ {Th}} {R_ {Th} + R_L} $ vào phương trình trên.

$$ P_L = \ lgroup \ frac {V_ {Th}} {(R_ {Th} + R_L)} \ rgroup ^ 2 R_L $$

$ \ Rightarrow P_L = {V_ {Th}} ^ 2 \ lbrace \ frac {R_L} {(R_ {Th} + R_L) ^ 2} \ rbrace $ Equation 1

Điều kiện để truyền điện tối đa

Đối với cực đại hoặc cực tiểu, đạo hàm đầu tiên sẽ bằng không. Vì vậy, hãy phân biệt Công thức 1 với R _L và làm cho nó bằng không.

$$ \ frac {dP_L} {dR_L} = {V_ {Th}} ^ 2 \ lbrace \ frac {(R_ {Th} + R_L) ^ 2 \ times 1 - R_L \ times 2 (R_ {Th} + R_L) } {(R_ {Th} + R_L) ^ 4} \ rbrace = 0 $$

$$ \ Rightarrow (R_ {Th} + R_L) ^ 2 -2R_L (R_ {Th} + R_L) = 0 $$

$$ \ Rightarrow (R_ {Th} + R_L) (R_ {Th} + R_L - 2R_L) = 0 $$

$$ \ Rightarrow (R_ {Th} - R_L) = 0 $$

$$ \ Rightarrow R_ {Th} = R_L \: hoặc \: R_L = R_ {Th} $$

Do đó, condition for maximum powertiêu tán trên tải là $ R_L = R_ {Th} $. Điều đó có nghĩa là, nếu giá trị của điện trở tải bằng giá trị của điện trở nguồn, tức là điện trở của Thevenin, thì công suất tiêu tán trên tải sẽ có giá trị lớn nhất.

Giá trị của truyền điện tối đa

Thay thế $ R_L = R_ {Th} \: \ & \: P_L = P_ {L, Max} $ trong Phương trình 1.

$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {(R_ {Th} + R_ {Th}) ^ 2} \ rbrace $$

$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {4 {R_ {Th}} ^ 2} \ rbrace $$

$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$

$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {L}}, \: kể từ khi \: R_ {L} = R_ {Th} $$

Do đó, maximum amount of power chuyển tải là

$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4R_ {L}} = \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} $$

Hiệu quả truyền điện tối đa

Chúng ta có thể tính toán hiệu suất của việc truyền công suất tối đa, $ \ eta_ {Max} $ bằng công thức sau.

$ \ eta_ {Max} = \ frac {P_ {L, Max}} {P_S} $ Equation 2

Ở đâu,

$ P_ {L, Max} $ là công suất lớn nhất truyền cho tải.
$ P_S $ là công suất do nguồn tạo ra.

Các amount of power generated bởi nguồn là

$$ P_S = I ^ 2 R_ {Th} + I ^ 2 R_L $$

$$ \ Rightarrow P_S = 2 I ^ 2 R_ {Th}, \: kể từ \: R_ {L} = R_ {Th} $$

Thay $ I = \ frac {V_ {Th}} {2 R_ {Th}} $ vào phương trình trên.

$$ P_S = 2 \ lgroup \ frac {V_ {Th}} {2 R_ {Th}} \ rgroup ^ 2 R_ {Th} $$

$$ \ Rightarrow P_S = 2 \ lgroup \ frac {{V_ {Th}} ^ 2} {4 {R_ {Th}} ^ 2} \ rgroup R_ {Th} $$

$$ \ Rightarrow P_S = \ frac {{V_ {Th}} ^ 2} {2 R_ {Th}} $$

Thay các giá trị của $ P_ {L, Max} $ và $ P_S $ trong Phương trình 2.

$$ \ eta_ {Max} = \ frac {\ lgroup \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} \ rgroup} {\ lgroup \ frac {{V_ {Th}} ^ 2} { 2R_ {Th}} \ rgroup} $$

$$ \ Rightarrow \ eta_ {Max} = \ frac {1} {2} $$

Chúng tôi có thể thể hiện hiệu quả của việc truyền tải điện năng tối đa về mặt percentage như sau -

$$ \% \ eta_ {Max} = \ eta_ {Max} \ lần 100 \% $$

$$ \ Rightarrow \% \ eta_ {Max} = \ lgroup \ frac {1} {2} \ rgroup \ times 100 \% $$

$$ \ Rightarrow \% \ eta_ {Max} = 50 \% $$

Do đó, hiệu suất truyền tải điện năng tối đa là 50 %.

Thí dụ

Tìm maximum powermà có thể mắc vào điện trở tải R _L của đoạn mạch như hình sau.

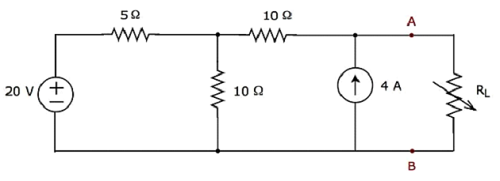
Step 1- Trong chương Định lý Thevenin, chúng ta đã tính toán mạch tương đương của Thevenin ở phía bên trái của các đầu cuối A & B. Chúng ta có thể sử dụng mạch này ngay bây giờ. Nó được hiển thị trong hình sau.

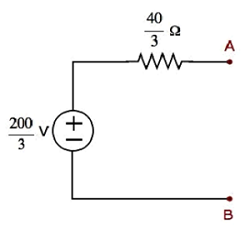
Ở đây, điện áp của Thevenin $ V_ {Th} = \ frac {200} {3} V $ và điện trở của Thevenin $ R_ {Th} = \ frac {40} {3} \ Omega $

Step 2- Thay phần mạch điện nằm bên trái của các cực A & B của đoạn mạch đã cho bằng đoạn mạch tương đương của Thevenin ở trên. Sơ đồ mạch kết quả được hiển thị trong hình sau.

Step 3- Chúng ta có thể tìm công suất cực đại sẽ cung cấp cho điện trở tải, R _L bằng công thức sau.

$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$

Thay thế $ V_ {Th} = \ frac {200} {3} V $ và $ R_ {Th} = \ frac {40} {3} \ Omega $ trong công thức trên.

$$ P_ {L, Max} = \ frac {\ lgroup \ frac {200} {3} \ rgroup ^ 2} {4 \ lgroup \ frac {40} {3} \ rgroup} $$

$$ P_ {L, Max} = \ frac {250} {3} W $$

Do đó, maximum power sẽ được đưa đến điện trở tải RL của mạch đã cho là $ \ mathbf {\ frac {250} {3}} $ W