Lý thuyết mạng - Yếu tố thụ động
Trong chương này, chúng ta sẽ thảo luận chi tiết về các phần tử thụ động như Điện trở, Cuộn cảm và Tụ điện. Chúng ta hãy bắt đầu với Điện trở.
Điện trở
Chức năng chính của Điện trở là chống lại hoặc hạn chế dòng điện. Do đó, các điện trở được sử dụng để hạn chế lượng dòng điện và / hoặc phân chia (chia sẻ) điện áp.
Cho cường độ dòng điện chạy qua điện trở là I ampe và hiệu điện thế trên nó là V vôn. Cácsymbol của điện trở cùng với dòng điện, I và hiệu điện thế, V được thể hiện trong hình sau.
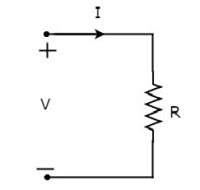
Dựa theo Ohm’s law, hiệu điện thế trên điện trở là tích của dòng điện chạy qua nó và điện trở của điện trở đó. Mathematically, nó có thể được biểu thị là
$ V = IR $ Equation 1
$ \ Rightarrow I = \ frac {V} {R} $Equation 2
Ở đâu, R là điện trở của một điện trở.
Từ phương trình 2, chúng ta có thể kết luận rằng dòng điện chạy qua điện trở tỷ lệ thuận với điện áp đặt trên điện trở và tỷ lệ nghịch với điện trở của điện trở.
Power trong một phần tử mạch điện có thể được biểu diễn dưới dạng
$ P = VI $Equation 3
Thay thế, Phương trình 1 trong Phương trình 3.
$ P = (IR) I $
$ \ Rightarrow P = I ^ 2 R $ Equation 4
Thay thế, Phương trình 2 trong Phương trình 3.
$ P = V \ lgroup \ frac {V} {R} \ rgroup $
$ \ Rightarrow P = \ frac {V ^ 2} {R} $ Equation 5
Vì vậy, chúng ta có thể tính toán lượng điện năng tiêu tán trong điện trở bằng cách sử dụng một trong các công thức được đề cập trong phương trình 3 đến 5.
Cuộn cảm
Nói chung, cuộn cảm sẽ có số vòng dây. Do đó, chúng tạo ra từ thông khi dòng điện chạy qua nó. Vì vậy, tổng lượng từ thông tạo ra bởi một cuộn cảm phụ thuộc vào dòng điện chạy qua nó và chúng có mối quan hệ tuyến tính.
Mathematically, nó có thể được viết là
$$ \ Psi \: \ alpha \: I $$
$$ \ Rightarrow \ Psi = LI $$
Ở đâu,
Ψ là tổng từ thông
L là độ tự cảm của cuộn cảm
Cho cường độ dòng điện chạy qua cuộn cảm là I ampe và hiệu điện thế qua cuộn cảm là V vôn. Cácsymbolcủa cuộn cảm cùng với dòng điện I và hiệu điện thế V được biểu diễn trong hình sau.
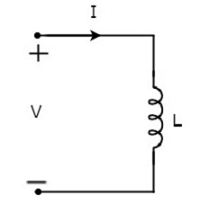
Dựa theo Faraday’s law, điện áp trên cuộn cảm có thể được viết là
$$ V = \ frac {d \ Psi} {dt} $$
Thay Ψ = LI vào phương trình trên.
$$ V = \ frac {d (LI)} {dt} $$
$$ \ Rightarrow V = L \ frac {dI} {dt} $$
$$ \ Rightarrow I = \ frac {1} {L} \ int V dt $$
Từ các phương trình trên, chúng ta có thể kết luận rằng tồn tại một linear relationship giữa điện áp trên cuộn cảm và dòng điện chạy qua nó.
Chúng ta biết rằng power trong một phần tử mạch điện có thể được biểu diễn dưới dạng
$$ P = VI $$
Thay $ V = L \ frac {dI} {dt} $ vào phương trình trên.
$$ P = \ lgroup L \ frac {dI} {dt} \ rgroup I $$
$$ \ Rightarrow P = LI \ frac {dI} {dt} $$
Bằng cách tích phân phương trình trên, chúng ta sẽ nhận được energy được lưu trữ trong một cuộn cảm như
$$ W = \ frac {1} {2} LI ^ 2 $$
Vì vậy, cuộn cảm lưu trữ năng lượng dưới dạng từ trường.
Tụ điện
Nói chung, tụ điện có hai bản dẫn điện, ngăn cách nhau bằng môi trường điện môi. Nếu điện áp dương được đặt trên tụ điện, thì nó lưu trữ điện tích dương. Tương tự, nếu điện áp âm được đặt trên tụ điện, thì nó sẽ tích trữ điện tích âm.
Vì vậy, lượng điện tích lưu trữ trong tụ điện phụ thuộc vào điện áp đặt vào Vxuyên qua nó và chúng có mối quan hệ tuyến tính. Về mặt toán học, nó có thể được viết là
$$ Q \: \ alpha \: V $$
$$ \ Rightarrow Q = CV $$
Ở đâu,
Q là điện tích được lưu trữ trong tụ điện.
C là điện dung của tụ điện.
Cho cường độ dòng điện chạy qua tụ điện là I ampe và hiệu điện thế qua tụ là V vôn. Kí hiệu của tụ điện cùng với dòng điện I và hiệu điện thế V được thể hiện trong hình sau.
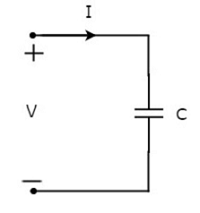
Chúng tôi biết rằng current không là gì ngoài time rate of flow of charge. Về mặt toán học, nó có thể được biểu diễn dưới dạng
$$ I = \ frac {dQ} {dt} $$
Thay $ Q = CV $ vào phương trình trên.
$$ I = \ frac {d (CV)} {dt} $$
$$ \ Rightarrow I = C \ frac {dV} {dt} $$
$$ \ Rightarrow V = \ frac {1} {C} \ int I dt $$
Từ các phương trình trên, chúng ta có thể kết luận rằng tồn tại một linear relationship giữa hiệu điện thế trên tụ điện và cường độ dòng điện chạy qua nó.
Chúng ta biết rằng power trong một phần tử mạch điện có thể được biểu diễn dưới dạng
$$ P = VI $$
Thay $ I = C \ frac {dV} {dt} $ vào phương trình trên.
$$ P = V \ lgroup C \ frac {dV} {dt} \ rgroup $$
$$ \ Rightarrow P = CV \ frac {dV} {dt} $$
Bằng cách tích phân phương trình trên, chúng ta sẽ nhận được energy được lưu trữ trong tụ điện như
$$ W = \ frac {1} {2} CV ^ 2 $$
Vì vậy, tụ điện lưu trữ năng lượng dưới dạng điện trường.